
Concept explainers
(a)
The domain points of the given function appear to be differentiable.
(a)
Answer to Problem 9E
The required domain points of the given function appears to be differentiable is
Explanation of Solution
Given information:
The given function is:
And, the domain points is
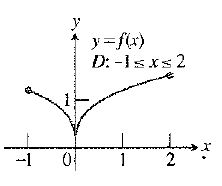
The given function is:
Since, from the figure it is seen that the function
Also, from the figure it is seen that the function
Thus, the function
Hence, the required domain of the function appears to be differentiable is
(b)
The domain points of the given function appear to be continuous but not differentiable.
(b)
Answer to Problem 9E
The required domain of the given function appears to be continuous but not differentiable is
Explanation of Solution
Given information:
The given function is:
And, the domain points is
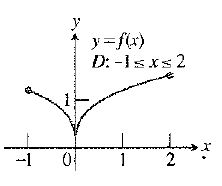
The given function is
From the results (a) it is seen that the function
Since, the given function has discontinuities at
Also, the given function
Thus, the given function
Hence, the required domain of the function whether the function appears to be continuous but not differentiable is
(c)
The domain of the given function appear neither continuous nor differentiable.
(c)
Answer to Problem 9E
The required domain of the given function appears to be neither continuous nor differentiable is none.
Explanation of Solution
Given information:
The given function is:
And, the domain points is
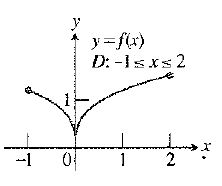
The given function is
From the graph it is seen that the given function
Thus, there are no points where the function is neither continuous nor differentiable.
Hence, required domain of the given function appears neither continuous nor differentiable is none.
Chapter 3 Solutions
Calculus: Graphical, Numerical, Algebraic
Additional Math Textbook Solutions
Elementary Statistics: Picturing the World (7th Edition)
University Calculus: Early Transcendentals (4th Edition)
Basic Business Statistics, Student Value Edition
Elementary Statistics
Elementary Statistics (13th Edition)
Pre-Algebra Student Edition
- Prove 11.1.2arrow_forward39. (a) Show that Σeak converges for each α > 0. (b) Show that keak converges for each a > 0. k=0 (c) Show that, more generally, Σk"eak converges for each k=0 nonnegative integer n and each a > 0.arrow_forward#3 Find the derivative y' = of the following functions, using the derivative rules: dx a) y-Cos 6x b) y=x-Sin4x c) y=x-Cos3x d) y=x-R CD-X:-:TCH :D:D:D - Sin f) Sin(x²) (9) Tan (x³)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





