Calculus: Graphical, Numerical, Algebraic

3rd Edition

ISBN: 9780133688399

Author: Finney, Ross L.

Publisher: Pearson/Prentice Hall

See similar textbooks

Concept explainers

Minimization

In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in ter…

Maxima and Minima

The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.

Derivatives

A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which …

Concavity

In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the …

Videos

Question

Chapter 3.1, Problem 21E

(a)

To determine

Tocalculate:The time rate and the date on which the amount of daylight increasing at the fastest rate.

(a)

Expert Solution

Answer to Problem 21E

The required date is April 1^s^t; and the rate is 0.15 hours per day.

Explanation of Solution

Given information:

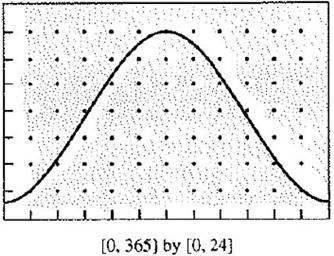
Starting period is January 1.

End period is December 31.

Each vertical ticks corresponds to 3 hours.

Each month has 30 days.

Daylight graph

Calculus: Graphical, Numerical, Algebraic, Chapter 3.1, Problem 21E , additional homework tip 1

Formula Used:

Slop formula of a straight line:

Slop between two points (x1,y1) and (x2,y2) is

m=y2−y1x2−x1 , where m represent the slop of the line connecting the points (x1,y1) and (x2,y2) .

Calculation:

At the highest point where the graph has the steepest positive curve, the sum of daylight would grow. From the given graph steepest points is at x=90 .

Given that each month has 30 days, represented by the horizontal ticks.

Thus, after 90 days the month will be April 1.

Now, find the slop at that point,

Here each vertical tick corresponds to 3 hours.

Consider the points of the graph 30 days before and 30 days later than April 1.

Consider 30 days before

Thus the points are (60, 6) and (120, 15).

Calculate the slop between these points. Use the slop formula of a straight line.

m=15−6120−60=960=320=0.15

Hence, the required date is April 1^s^t; and the rate is 0.15 hours per day.

(b)

To determine

The days on which the rate of change in the amount of daylight is zero.

(b)

Expert Solution

Answer to Problem 21E

The required days are January 1 and July 1.

Explanation of Solution

Given information:

Starting period is January 1.

End period is December 31.

Each vertical ticks corresponds to 3 hours.

Each month has 30 days.

Daylight graph

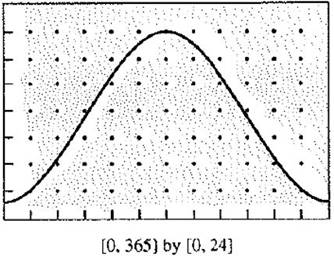
Calculus: Graphical, Numerical, Algebraic, Chapter 3.1, Problem 21E , additional homework tip 2

If the slop of the graph is zero, the rate of change will be zero.

In the graph the points where the graphstops increasing and starts decreasing or stop decreasing and starts increasing, slop will zero.

There are two points where the slop is zero. These are at x=0 and x=180 .

Now, find the month at x=0 and x=180 .

From the graph at x=0 , date is January 1.

At x=180 , date is July 1.

Hence, the required days are January 1 and July 1.

(c)

To determine

The dates on which the rate of change in the number of daylight hours positive.

(c)

Expert Solution

Answer to Problem 21E

The rate of change is positive from January 1 to 30 June and the negative rate of change is from July 1 to 31 December.

Explanation of Solution

Given information:

Starting period is January 1.

End period is December 31.

Each vertical ticks corresponds to 3 hours.

Each month has 30 days.

Daylight graph

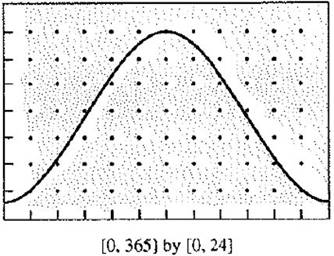
Calculus: Graphical, Numerical, Algebraic, Chapter 3.1, Problem 21E , additional homework tip 3

Find the positive rate of change.

The exchange rate is positive where the graph increases. From the graph it can be seen that the curve is increases from 1 January until 30 June.

Thus, the rate is positive from 1 January to 30 June.

Similarly find the negative rate of change.

The exchange rate is negative if the graph reduces. From the graph it can be seen that the curve is decreases from 1 July to 31 December.

Hence, the rate of change is positive from January 1 to 30 June and the negative rate of change is from July 1 to 31 December.

Conclusion:

Chapter 3.1, Problem 20E

Chapter 3.1, Problem 22E

Chapter 3 Solutions

Calculus: Graphical, Numerical, Algebraic

Ch. 3.1 - Prob. 1QR Ch. 3.1 - Prob. 2QR Ch. 3.1 - Prob. 3QR Ch. 3.1 - Prob. 4QR Ch. 3.1 - Prob. 5QR Ch. 3.1 - Prob. 6QR Ch. 3.1 - Prob. 7QR Ch. 3.1 - Prob. 8QR Ch. 3.1 - Prob. 9QR Ch. 3.1 - Prob. 10QR

Ch. 3.1 - Prob. 1E Ch. 3.1 - Prob. 2E Ch. 3.1 - Prob. 3E Ch. 3.1 - Prob. 4E Ch. 3.1 - Prob. 5E Ch. 3.1 - Prob. 6E Ch. 3.1 - Prob. 7E Ch. 3.1 - Prob. 8E Ch. 3.1 - Prob. 9E Ch. 3.1 - Prob. 10E Ch. 3.1 - Prob. 11E Ch. 3.1 - Prob. 12E Ch. 3.1 - Prob. 13E Ch. 3.1 - Prob. 14E Ch. 3.1 - Prob. 15E Ch. 3.1 - Prob. 16E Ch. 3.1 - Prob. 17E Ch. 3.1 - Prob. 18E Ch. 3.1 - Prob. 19E Ch. 3.1 - Prob. 20E Ch. 3.1 - Prob. 21E Ch. 3.1 - Prob. 22E Ch. 3.1 - Prob. 23E Ch. 3.1 - Prob. 24E Ch. 3.1 - Prob. 25E Ch. 3.1 - Prob. 26E Ch. 3.1 - Prob. 27E Ch. 3.1 - Prob. 28E Ch. 3.1 - Prob. 29E Ch. 3.1 - Prob. 30E Ch. 3.1 - Prob. 31E Ch. 3.1 - Prob. 32E Ch. 3.1 - Prob. 33E Ch. 3.1 - Prob. 34E Ch. 3.1 - Prob. 35E Ch. 3.1 - Prob. 36E Ch. 3.1 - Prob. 37E Ch. 3.1 - Prob. 38E Ch. 3.1 - Prob. 39E Ch. 3.1 - Prob. 40E Ch. 3.1 - Prob. 41E Ch. 3.1 - Prob. 42E Ch. 3.1 - Prob. 43E Ch. 3.1 - Prob. 44E Ch. 3.1 - Prob. 45E Ch. 3.2 - Prob. 1QR Ch. 3.2 - Prob. 2QR Ch. 3.2 - Prob. 3QR Ch. 3.2 - Prob. 4QR Ch. 3.2 - Prob. 5QR Ch. 3.2 - Prob. 6QR Ch. 3.2 - Prob. 7QR Ch. 3.2 - Prob. 8QR Ch. 3.2 - Prob. 9QR Ch. 3.2 - Prob. 10QR Ch. 3.2 - Prob. 1E Ch. 3.2 - Prob. 2E Ch. 3.2 - Prob. 3E Ch. 3.2 - Prob. 4E Ch. 3.2 - Prob. 5E Ch. 3.2 - Prob. 6E Ch. 3.2 - Prob. 7E Ch. 3.2 - Prob. 8E Ch. 3.2 - Prob. 9E Ch. 3.2 - Prob. 10E Ch. 3.2 - Prob. 11E Ch. 3.2 - Prob. 12E Ch. 3.2 - Prob. 13E Ch. 3.2 - Prob. 14E Ch. 3.2 - Prob. 15E Ch. 3.2 - Prob. 16E Ch. 3.2 - Prob. 17E Ch. 3.2 - Prob. 18E Ch. 3.2 - Prob. 19E Ch. 3.2 - Prob. 20E Ch. 3.2 - Prob. 21E Ch. 3.2 - Prob. 22E Ch. 3.2 - Prob. 23E Ch. 3.2 - Prob. 24E Ch. 3.2 - Prob. 25E Ch. 3.2 - Prob. 26E Ch. 3.2 - Prob. 27E Ch. 3.2 - Prob. 28E Ch. 3.2 - Prob. 29E Ch. 3.2 - Prob. 30E Ch. 3.2 - Prob. 31E Ch. 3.2 - Prob. 32E Ch. 3.2 - Prob. 33E Ch. 3.2 - Prob. 34E Ch. 3.2 - Prob. 35E Ch. 3.2 - Prob. 36E Ch. 3.2 - Prob. 37E Ch. 3.2 - Prob. 38E Ch. 3.2 - Prob. 39E Ch. 3.2 - Prob. 40E Ch. 3.2 - Prob. 41E Ch. 3.2 - Prob. 42E Ch. 3.2 - Prob. 43E Ch. 3.2 - Prob. 44E Ch. 3.2 - Prob. 45E Ch. 3.2 - Prob. 46E Ch. 3.2 - Prob. 47E Ch. 3.2 - Prob. 48E Ch. 3.3 - Prob. 1QR Ch. 3.3 - Prob. 2QR Ch. 3.3 - Prob. 3QR Ch. 3.3 - Prob. 4QR Ch. 3.3 - Prob. 5QR Ch. 3.3 - Prob. 6QR Ch. 3.3 - Prob. 7QR Ch. 3.3 - Prob. 8QR Ch. 3.3 - Prob. 9QR Ch. 3.3 - Prob. 10QR Ch. 3.3 - Prob. 1E Ch. 3.3 - Prob. 2E Ch. 3.3 - Prob. 3E Ch. 3.3 - Prob. 4E Ch. 3.3 - Prob. 5E Ch. 3.3 - Prob. 6E Ch. 3.3 - Prob. 7E Ch. 3.3 - Prob. 8E Ch. 3.3 - Prob. 9E Ch. 3.3 - Prob. 10E Ch. 3.3 - Prob. 11E Ch. 3.3 - Prob. 12E Ch. 3.3 - Prob. 13E Ch. 3.3 - Prob. 14E Ch. 3.3 - Prob. 15E Ch. 3.3 - Prob. 16E Ch. 3.3 - Prob. 17E Ch. 3.3 - Prob. 18E Ch. 3.3 - Prob. 19E Ch. 3.3 - Prob. 20E Ch. 3.3 - Prob. 21E Ch. 3.3 - Prob. 22E Ch. 3.3 - Prob. 23E Ch. 3.3 - Prob. 24E Ch. 3.3 - Prob. 25E Ch. 3.3 - Prob. 26E Ch. 3.3 - Prob. 27E Ch. 3.3 - Prob. 28E Ch. 3.3 - Prob. 29E Ch. 3.3 - Prob. 30E Ch. 3.3 - Prob. 31E Ch. 3.3 - Prob. 32E Ch. 3.3 - Prob. 33E Ch. 3.3 - Prob. 34E Ch. 3.3 - Prob. 35E Ch. 3.3 - Prob. 36E Ch. 3.3 - Prob. 37E Ch. 3.3 - Prob. 38E Ch. 3.3 - Prob. 39E Ch. 3.3 - Prob. 40E Ch. 3.3 - Prob. 41E Ch. 3.3 - Prob. 42E Ch. 3.3 - Prob. 43E Ch. 3.3 - Prob. 44E Ch. 3.3 - Prob. 45E Ch. 3.3 - Prob. 46E Ch. 3.3 - Prob. 47E Ch. 3.3 - Prob. 48E Ch. 3.3 - Prob. 49E Ch. 3.3 - Prob. 50E Ch. 3.3 - Prob. 51E Ch. 3.3 - Prob. 52E Ch. 3.3 - Prob. 53E Ch. 3.3 - Prob. 54E Ch. 3.3 - Prob. 55E Ch. 3.3 - Prob. 56E Ch. 3.3 - Prob. 57E Ch. 3.3 - Prob. 58E Ch. 3.3 - Prob. 59E Ch. 3.3 - Prob. 1QQ Ch. 3.3 - Prob. 2QQ Ch. 3.3 - Prob. 3QQ Ch. 3.3 - Prob. 4QQ Ch. 3.4 - Prob. 1QR Ch. 3.4 - Prob. 2QR Ch. 3.4 - Prob. 3QR Ch. 3.4 - Prob. 4QR Ch. 3.4 - Prob. 5QR Ch. 3.4 - Prob. 6QR Ch. 3.4 - Prob. 7QR Ch. 3.4 - Prob. 8QR Ch. 3.4 - Prob. 9QR Ch. 3.4 - Prob. 10QR Ch. 3.4 - Prob. 1E Ch. 3.4 - Prob. 2E Ch. 3.4 - Prob. 3E Ch. 3.4 - Prob. 4E Ch. 3.4 - Prob. 5E Ch. 3.4 - Prob. 6E Ch. 3.4 - Prob. 7E Ch. 3.4 - Prob. 8E Ch. 3.4 - Prob. 9E Ch. 3.4 - Prob. 10E Ch. 3.4 - Prob. 11E Ch. 3.4 - Prob. 12E Ch. 3.4 - Prob. 13E Ch. 3.4 - Prob. 14E Ch. 3.4 - Prob. 15E Ch. 3.4 - Prob. 16E Ch. 3.4 - Prob. 17E Ch. 3.4 - Prob. 18E Ch. 3.4 - Prob. 19E Ch. 3.4 - Prob. 20E Ch. 3.4 - Prob. 21E Ch. 3.4 - Prob. 22E Ch. 3.4 - Prob. 23E Ch. 3.4 - Prob. 24E Ch. 3.4 - Prob. 25E Ch. 3.4 - Prob. 26E Ch. 3.4 - Prob. 27E Ch. 3.4 - Prob. 28E Ch. 3.4 - Prob. 29E Ch. 3.4 - Prob. 30E Ch. 3.4 - Prob. 31E Ch. 3.4 - Prob. 32E Ch. 3.4 - Prob. 33E Ch. 3.4 - Prob. 34E Ch. 3.4 - Prob. 35E Ch. 3.4 - Prob. 36E Ch. 3.4 - Prob. 37E Ch. 3.4 - Prob. 38E Ch. 3.4 - Prob. 39E Ch. 3.4 - Prob. 40E Ch. 3.4 - Prob. 41E Ch. 3.4 - Prob. 42E Ch. 3.4 - Prob. 43E Ch. 3.4 - Prob. 44E Ch. 3.4 - Prob. 45E Ch. 3.4 - Prob. 46E Ch. 3.4 - Prob. 47E Ch. 3.4 - Prob. 48E Ch. 3.4 - Prob. 49E Ch. 3.4 - Prob. 50E Ch. 3.5 - Prob. 1QR Ch. 3.5 - Prob. 2QR Ch. 3.5 - Prob. 3QR Ch. 3.5 - Prob. 4QR Ch. 3.5 - Prob. 5QR Ch. 3.5 - Prob. 6QR Ch. 3.5 - Prob. 7QR Ch. 3.5 - Prob. 8QR Ch. 3.5 - Prob. 9QR Ch. 3.5 - Prob. 10QR Ch. 3.5 - Prob. 1E Ch. 3.5 - Prob. 2E Ch. 3.5 - Prob. 3E Ch. 3.5 - Prob. 4E Ch. 3.5 - Prob. 5E Ch. 3.5 - Prob. 6E Ch. 3.5 - Prob. 7E Ch. 3.5 - Prob. 8E Ch. 3.5 - Prob. 9E Ch. 3.5 - Prob. 10E Ch. 3.5 - Prob. 11E Ch. 3.5 - Prob. 12E Ch. 3.5 - Prob. 13E Ch. 3.5 - Prob. 14E Ch. 3.5 - Prob. 15E Ch. 3.5 - Prob. 16E Ch. 3.5 - Prob. 17E Ch. 3.5 - Prob. 18E Ch. 3.5 - Prob. 19E Ch. 3.5 - Prob. 20E Ch. 3.5 - Prob. 21E Ch. 3.5 - Prob. 22E Ch. 3.5 - Prob. 23E Ch. 3.5 - Prob. 24E Ch. 3.5 - Prob. 25E Ch. 3.5 - Prob. 26E Ch. 3.5 - Prob. 27E Ch. 3.5 - Prob. 28E Ch. 3.5 - Prob. 29E Ch. 3.5 - Prob. 30E Ch. 3.5 - Prob. 31E Ch. 3.5 - Prob. 32E Ch. 3.5 - Prob. 33E Ch. 3.5 - Prob. 34E Ch. 3.5 - Prob. 35E Ch. 3.5 - Prob. 36E Ch. 3.5 - Prob. 37E Ch. 3.5 - Prob. 38E Ch. 3.5 - Prob. 39E Ch. 3.5 - Prob. 40E Ch. 3.5 - Prob. 41E Ch. 3.5 - Prob. 42E Ch. 3.5 - Prob. 43E Ch. 3.5 - Prob. 44E Ch. 3.5 - Prob. 45E Ch. 3.5 - Prob. 46E Ch. 3.5 - Prob. 47E Ch. 3.5 - Prob. 48E Ch. 3.5 - Prob. 49E Ch. 3.5 - Prob. 50E Ch. 3.5 - Prob. 51E Ch. 3.5 - Prob. 52E Ch. 3.5 - Prob. 1QQ Ch. 3.5 - Prob. 2QQ Ch. 3.5 - Prob. 3QQ Ch. 3.5 - Prob. 4QQ Ch. 3 - Prob. 1RE Ch. 3 - Prob. 2RE Ch. 3 - Prob. 3RE Ch. 3 - Prob. 4RE Ch. 3 - Prob. 5RE Ch. 3 - Prob. 6RE Ch. 3 - Prob. 7RE Ch. 3 - Prob. 8RE Ch. 3 - Prob. 9RE Ch. 3 - Prob. 10RE Ch. 3 - Prob. 11RE Ch. 3 - Prob. 12RE Ch. 3 - Prob. 13RE Ch. 3 - Prob. 14RE Ch. 3 - Prob. 15RE Ch. 3 - Prob. 16RE Ch. 3 - Prob. 17RE Ch. 3 - Prob. 18RE Ch. 3 - Prob. 19RE Ch. 3 - Prob. 20RE Ch. 3 - Prob. 21RE Ch. 3 - Prob. 22RE Ch. 3 - Prob. 23RE Ch. 3 - Prob. 24RE Ch. 3 - Prob. 25RE Ch. 3 - Prob. 26RE Ch. 3 - Prob. 27RE Ch. 3 - Prob. 28RE Ch. 3 - Prob. 29RE Ch. 3 - Prob. 30RE Ch. 3 - Prob. 31RE Ch. 3 - Prob. 32RE Ch. 3 - Prob. 33RE Ch. 3 - Prob. 34RE Ch. 3 - Prob. 35RE Ch. 3 - Prob. 36RE Ch. 3 - Prob. 37RE Ch. 3 - Prob. 38RE Ch. 3 - Prob. 39RE Ch. 3 - Prob. 40RE Ch. 3 - Prob. 41RE Ch. 3 - Prob. 42RE Ch. 3 - Prob. 43RE Ch. 3 - Prob. 44RE Ch. 3 - Prob. 45RE Ch. 3 - Prob. 46RE Ch. 3 - Prob. 47RE Ch. 3 - Prob. 48RE Ch. 3 - Prob. 49RE Ch. 3 - Prob. 50RE Ch. 3 - Prob. 51RE Ch. 3 - Prob. 52RE Ch. 3 - Prob. 53RE Ch. 3 - Prob. 54RE Ch. 3 - Prob. 55RE Ch. 3 - Prob. 56RE Ch. 3 - Prob. 57RE Ch. 3 - Prob. 58RE Ch. 3 - Prob. 59RE Ch. 3 - Prob. 60RE Ch. 3 - Prob. 61RE Ch. 3 - Prob. 62RE Ch. 3 - Prob. 63RE Ch. 3 - Prob. 64RE Ch. 3 - Prob. 65RE Ch. 3 - Prob. 66RE Ch. 3 - Prob. 67RE Ch. 3 - Prob. 68RE Ch. 3 - Prob. 69RE Ch. 3 - Prob. 70RE Ch. 3 - Prob. 71RE Ch. 3 - Prob. 72RE Ch. 3 - Prob. 73RE Ch. 3 - Prob. 74RE Ch. 3 - Prob. 75RE Ch. 3 - Prob. 76RE Ch. 3 - Prob. 77RE Ch. 3 - Prob. 78RE Ch. 3 - Prob. 79RE Ch. 3 - Prob. 80RE Ch. 3 - Prob. 81RE Ch. 3 - Prob. 82RE Ch. 3 - Prob. 83RE

Additional Math Textbook Solutions

Find more solutions based on key concepts

The table by using the given graph of h.

Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)

Seven different gifts are to be distributed among 10 children. How many distinct results are possible if no chi...

A First Course in Probability (10th Edition)

Read about basic ideas of statistics in Common Core Standards for grades 3-5, and discuss why students at these...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

2. Source of Data In conducting a statistical study, why is it important to consider the source of the data?

Elementary Statistics

A linear equation is solved by using the intersection of graphs method. Find the solution by interpreting the g...

College Algebra with Modeling & Visualization (5th Edition)

Balloons A spherical balloon is inflated and its volume increases at a rate of 15 in3/min. What is the rate of ...

Calculus: Early Transcendentals (2nd Edition)

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.