C++ for Engineers and Scientists
4th Edition
ISBN: 9781133187844
Author: Bronson, Gary J.
Publisher: Course Technology Ptr
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.3, Problem 8E
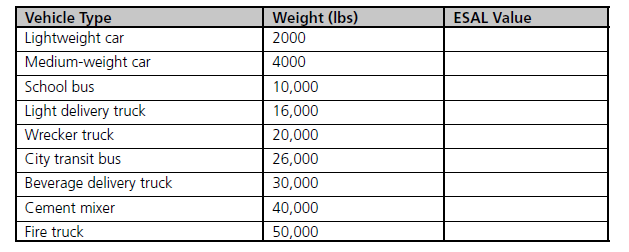
(Transportation) Road construction requires estimating the expected loads on a road’s pavement over its design life. A common approach for determining this information is to use ESAL values; one ESAL is the load a single 18,000-lb (80,000 N) single-axle truck applies to the road’s surface. The ESAL value for any single-axle vehicle can be approximated by this formula:
ESAL is the equivalent single-axle load.
W is the vehicle’s weight (lbs).
Using this formula, write, compile, and run a C++
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
using r language A continuous random variable X has density function f(x)=1/56(3x^2+4x^3+5x^4).0<=x<=2 (1) secify the density g of the random variable Y you find for the acceptance rejection method. (2) what is the value of c you choose to use for the acceptance rejection method (3) use the acceptance rejection method to generate a random sample of size 1000 from the distribution of X .graph the density histogram of the sample and compare it with the density function f(x)
using r language a continuous random variable X has density function f(x)=1/4x^3e^-(pi/2)^4,x>=0
derive the probability inverse transformation F^(-1)x where F(x) is the cdf of the random variable X
using r language in an accelerated failure test, components are operated under extreme conditions so that a substantial number will fail in a rather short time. in such a test involving two types of microships 600 chips manufactured by an existing process were tested and 125 of them failed then 800 chips manufactured by a new process were tested and 130 of them failed what is the 90%confidence interval for the difference between the proportions of failure for chips manufactured by two processes? using r language
Chapter 3 Solutions
C++ for Engineers and Scientists
Ch. 3.1 - (General math) Write an assignment statement to...Ch. 3.1 - (General math) Write an assignment statement to...Ch. 3.1 - (Conversion) Write an assignment statement to...Ch. 3.1 - Prob. 4ECh. 3.1 - (Physics) Write an assignment statement to...Ch. 3.1 - (Numerical) Write an assignment statement to...Ch. 3.1 - (Civil eng.) Write an assignment statement to...Ch. 3.1 - (Physics) Coulomb’s Law states that the force, F,...Ch. 3.1 - (Civil eng.) Write an assignment statement to...Ch. 3.1 - (Desk check) Determine the output of the following...
Ch. 3.1 - (Debug) Determine and correct the errors in the...Ch. 3.1 - Prob. 12ECh. 3.1 - Prob. 13ECh. 3.1 - (General math) The area of an ellipse (see Figure...Ch. 3.1 - Prob. 15ECh. 3.2 - Prob. 1ECh. 3.2 - Prob. 2ECh. 3.2 - (Practice) Write a C++ program that displays the...Ch. 3.2 - Prob. 4ECh. 3.2 - Prob. 5ECh. 3.2 - Prob. 6ECh. 3.2 - Prob. 7ECh. 3.2 - Prob. 8ECh. 3.2 - (Electrical eng.) The combined resistance of three...Ch. 3.2 - Prob. 10ECh. 3.2 - Prob. 11ECh. 3.2 - (Civil eng.) Write a C++ program to calculate and...Ch. 3.3 - Prob. 1ECh. 3.3 - Prob. 2ECh. 3.3 - (Practice) Write C++ statements for the following:...Ch. 3.3 - Prob. 4ECh. 3.3 - (General math) Write, compile, and run a C++...Ch. 3.3 - (General math) If a 20-foot ladder is placed on...Ch. 3.3 - (Physics) The maximum height reached by a ball...Ch. 3.3 - (Transportation) Road construction requires...Ch. 3.3 - Prob. 9ECh. 3.3 - Prob. 10ECh. 3.3 - Prob. 11ECh. 3.3 - Prob. 12ECh. 3.4 - Prob. 1ECh. 3.4 - (Practice) a. Write a C++ program that first...Ch. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - (General math) a. Write, compile, and run a C++...Ch. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - (Electrical eng.) For the series circuit shown in...Ch. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - Prob. 13ECh. 3.5 - Prob. 1ECh. 3.5 - Prob. 2ECh. 3.5 - Prob. 3ECh. 3.5 - Prob. 4ECh. 3.5 - Prob. 5ECh. 3.6 - Prob. 1ECh. 3.6 - (General math) The value of p can be approximated...Ch. 3.6 - Prob. 3ECh. 3.6 - (General math) The volume of oil stored in an...Ch. 3.6 - Prob. 5ECh. 3.6 - (General math) The perimeter, approximate surface...Ch. 3.6 - Prob. 7ECh. 3.6 - Prob. 8ECh. 3.6 - Prob. 9ECh. 3 - (General math) a. Write a C++ program to calculate...Ch. 3 - General math) a. Write a C++ program to calculate...Ch. 3 - (General math) Modify the program written for...Ch. 3 - (Biology) The number of bacteria, B, in a culture...Ch. 3 - Prob. 5PPCh. 3 - (Heat transfer) The formula developed in Exercise...Ch. 3 - Prob. 7PPCh. 3 - (Electrical eng.) a. The voltage gain of an...Ch. 3 - (Electrical eng.) a. Write, compile, and run a C++...Ch. 3 - (Electrical eng.) The amplification of electronic...Ch. 3 - (Acoustics) The loudness of a sound is measured in...Ch. 3 - (General math) a. A balance has the following...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- I want a picture of the tools and the pictures used Cisco Packet Tracer Smart Home Automation:o Connect a temperature sensor and a fan to a home gateway.o Configure the home gateway so that the fan is activated when the temperature exceedsa set threshold (e.g., 30°C).2. WiFi Network Configuration:o Set up a wireless LAN with a unique SSID.o Enable WPA2 encryption to secure the WiFi network.o Implement MAC address filtering to allow only specific clients to connect.3. WLC Configuration:o Deploy at least two wireless access points connected to a Wireless LAN Controller(WLC).o Configure the WLC to manage the APs, broadcast the configured SSID, and applyconsistent security settings across all APs.arrow_forwardA. What will be printed executing the code above?B. What is the simplest way to set a variable of the class Full_Date to January 26 2020?C. Are there any empty constructors in this class Full_Date?a. If there is(are) in which code line(s)?b. If there is not, how would an empty constructor be? (create the code lines for it)D. Can the command std::cout << d1.m << std::endl; be included after line 28 withoutcausing an error?a. If it can, what will be printed?b. If it cannot, how could this command be fixed?arrow_forwardCisco Packet Tracer Smart Home Automation:o Connect a temperature sensor and a fan to a home gateway.o Configure the home gateway so that the fan is activated when the temperature exceedsa set threshold (e.g., 30°C).2. WiFi Network Configuration:o Set up a wireless LAN with a unique SSID.o Enable WPA2 encryption to secure the WiFi network.o Implement MAC address filtering to allow only specific clients to connect.3. WLC Configuration:o Deploy at least two wireless access points connected to a Wireless LAN Controller(WLC).o Configure the WLC to manage the APs, broadcast the configured SSID, and applyconsistent security settings across all APs.arrow_forward
- Transform the TM below that accepts words over the alphabet Σ= {a, b} with an even number of a's and b's in order that the output tape head is positioned over the first letter of the input, if the word is accepted, and all letters a should be replaced by the letter x. For example, for the input aabbaa the tape and head at the end should be: [x]xbbxx z/z,R b/b,R F ① a/a,R b/b,R a/a, R a/a,R b/b.R K a/a,R L b/b,Rarrow_forwardGiven the C++ code below, create a TM that performs the same operation, i.e., given an input over the alphabet Σ= {a, b} it prints the number of letters b in binary. 1 #include 2 #include 3 4- int main() { std::cout > str; for (char c : str) { if (c == 'b') count++; 5 std::string str; 6 int count = 0; 7 char buffer [1000]; 8 9 10 11- 12 13 14 } 15 16- 17 18 19 } 20 21 22} std::string binary while (count > 0) { binary = std::to_string(count % 2) + binary; count /= 2; std::cout << binary << std::endl; return 0;arrow_forwardConsidering the CFG described below, answer the following questions. Σ = {a, b} • NT = {S} Productions: P1 S⇒aSa P2 P3 SbSb S⇒ a P4 S⇒ b A. List one sequence of productions that can accept the word abaaaba; B. Give three 5-letter words that can be accepted by this CFG; C. Create a Pushdown automaton capable of accepting the language accepted by this CFG.arrow_forward
- Given the FSA below, answer the following questions. b 1 3 a a b b с 2 A. Write a RegEx that is equivalent to this FSA as it is; B. Write a RegEx that is equivalent to this FSA removing the states and edges corresponding to the letter c. Note: To both items feel free to use any method you want, including analyzing which words are accepted by the FSA, to generate your RegEx.arrow_forward3) Finite State Automata Given the FSA below, answer the following questions. a b a b 0 1 2 b b 3 A. Give three 4-letter words that can be accepted by this FSA; B. Give three 4-letter words that cannot be accepted by this FSA; C. How could you describe the words accepted by this FSA? D. Is this FSA deterministic or non-deterministic?arrow_forwardConsidering the TM below, answer the following questions. a/x,R €/E,L €/E,R €/E,L x/E,R c/c,R b/E.L c/c,L x/x,R I J K L M F b/E.L D A. Give three 4-letter words that can be accepted by this TM; B. Give three 4-letter words that cannot be accepted by this TM; C. How could you describe the words accepted by this TM? D. What is the alphabet of the language accepted by this TM?arrow_forward
- What is the generator? Explain motor generator motorarrow_forwardThis battle room is focused on entry level tasks for a network analyst where you will be given trials and reconnaissance, sensor tuning, log aggregation, SIEM queries, and network analysis. For this week’s project, complete the following tasks: From your Project Ares portal, LOG IN Click on LAUNCH GAME. Select the region NORTH AMERICA Click on Battle School Under the BATTLE SCHOOL pop-up window, click on START TRAINING. Under the BATTLE ROOMS tile, click on ENTER. Under the NETWORK ANALYST tile, click on PLAY. Wait for the Battle Room to load. While loading, the BATTLE ROOM button will display red. Once the Battle Room is loaded, the BATTLE ROOM button will turn yellow and the center of the disk display will indicate CONNECTED. Click on the BATTLE ROOM button to enter the Battle Room. Below the TASKS folder, make sure you click on INSTRUCTIONS to download the Network Analyst Fundamentals material. In the Battle Room, under the TASKS menu select task INTRUSION DETECTION. Complete…arrow_forwardCreate a relationship between the common field (Technician Number) of the two tables. Make sure that each client must have 1 and only 1 technician assigned, and each technician can have multiple clients. 2. Create a query to show the Client Number, Client Name, Billed, Paid for clients in Anderson city. Save the query. 3. Create a query to show the Technician Number, Last Name, First Name, YTD Earnings for technicians whose Hourly Rate is greater than or equal to 30. Save the query. 4. Create a query to show Client Number, Client Name, Billed, Paid for clients whose technician number is 22 and whose Billed is over 300. Save the query. 5. Create a query to show the Technician Number, Last Name, First Name, Client Number, Client Name for clients whose technician number 23. Save the query. 6. Create a query to show the Technician Number, Last Name, First Name, Client Number, Client Name for clients whose technician number 23 or 29. Save the query Help please Microsoft office accessarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole
C++ for Engineers and Scientists
Computer Science
ISBN:9781133187844
Author:Bronson, Gary J.
Publisher:Course Technology Ptr
C++ Programming: From Problem Analysis to Program...
Computer Science
ISBN:9781337102087
Author:D. S. Malik
Publisher:Cengage Learning
Operations Research : Applications and Algorithms
Computer Science
ISBN:9780534380588
Author:Wayne L. Winston
Publisher:Brooks Cole
Boolean Algebra - Digital Logic and Logic Families - Industrial Electronics; Author: Ekeeda;https://www.youtube.com/watch?v=u7XnJos-_Hs;License: Standard YouTube License, CC-BY
Boolean Algebra 1 – The Laws of Boolean Algebra; Author: Computer Science;https://www.youtube.com/watch?v=EPJf4owqwdA;License: Standard Youtube License