C++ for Engineers and Scientists
4th Edition
ISBN: 9781133187844
Author: Bronson, Gary J.
Publisher: Course Technology Ptr
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.4, Problem 10E
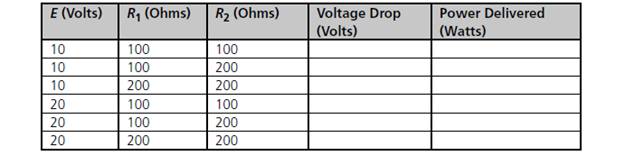
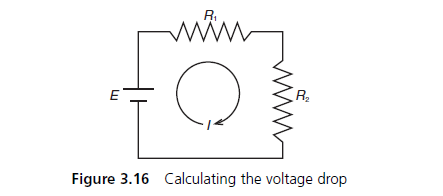
(Electrical eng.) For the series circuit shown in Figure 3.16, the voltage drop,
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
I need to resolve the following....You are trying to convince your boss that your company needs to invest in a license for MS-Project (project management software from Microsoft) before beginning a systems project. What arguments would you give her?
What are the four types of feasibility? what is the issues addressed by each feasibility component.
I would like to get ab example of a situation where Agile Methods might be preferable versus the traditional SDLC? What are the characteristics of this situation that give Agile Methods an advantage?
Chapter 3 Solutions
C++ for Engineers and Scientists
Ch. 3.1 - (General math) Write an assignment statement to...Ch. 3.1 - (General math) Write an assignment statement to...Ch. 3.1 - (Conversion) Write an assignment statement to...Ch. 3.1 - Prob. 4ECh. 3.1 - (Physics) Write an assignment statement to...Ch. 3.1 - (Numerical) Write an assignment statement to...Ch. 3.1 - (Civil eng.) Write an assignment statement to...Ch. 3.1 - (Physics) Coulomb’s Law states that the force, F,...Ch. 3.1 - (Civil eng.) Write an assignment statement to...Ch. 3.1 - (Desk check) Determine the output of the following...
Ch. 3.1 - (Debug) Determine and correct the errors in the...Ch. 3.1 - Prob. 12ECh. 3.1 - Prob. 13ECh. 3.1 - (General math) The area of an ellipse (see Figure...Ch. 3.1 - Prob. 15ECh. 3.2 - Prob. 1ECh. 3.2 - Prob. 2ECh. 3.2 - (Practice) Write a C++ program that displays the...Ch. 3.2 - Prob. 4ECh. 3.2 - Prob. 5ECh. 3.2 - Prob. 6ECh. 3.2 - Prob. 7ECh. 3.2 - Prob. 8ECh. 3.2 - (Electrical eng.) The combined resistance of three...Ch. 3.2 - Prob. 10ECh. 3.2 - Prob. 11ECh. 3.2 - (Civil eng.) Write a C++ program to calculate and...Ch. 3.3 - Prob. 1ECh. 3.3 - Prob. 2ECh. 3.3 - (Practice) Write C++ statements for the following:...Ch. 3.3 - Prob. 4ECh. 3.3 - (General math) Write, compile, and run a C++...Ch. 3.3 - (General math) If a 20-foot ladder is placed on...Ch. 3.3 - (Physics) The maximum height reached by a ball...Ch. 3.3 - (Transportation) Road construction requires...Ch. 3.3 - Prob. 9ECh. 3.3 - Prob. 10ECh. 3.3 - Prob. 11ECh. 3.3 - Prob. 12ECh. 3.4 - Prob. 1ECh. 3.4 - (Practice) a. Write a C++ program that first...Ch. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - (General math) a. Write, compile, and run a C++...Ch. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - (Electrical eng.) For the series circuit shown in...Ch. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - Prob. 13ECh. 3.5 - Prob. 1ECh. 3.5 - Prob. 2ECh. 3.5 - Prob. 3ECh. 3.5 - Prob. 4ECh. 3.5 - Prob. 5ECh. 3.6 - Prob. 1ECh. 3.6 - (General math) The value of p can be approximated...Ch. 3.6 - Prob. 3ECh. 3.6 - (General math) The volume of oil stored in an...Ch. 3.6 - Prob. 5ECh. 3.6 - (General math) The perimeter, approximate surface...Ch. 3.6 - Prob. 7ECh. 3.6 - Prob. 8ECh. 3.6 - Prob. 9ECh. 3 - (General math) a. Write a C++ program to calculate...Ch. 3 - General math) a. Write a C++ program to calculate...Ch. 3 - (General math) Modify the program written for...Ch. 3 - (Biology) The number of bacteria, B, in a culture...Ch. 3 - Prob. 5PPCh. 3 - (Heat transfer) The formula developed in Exercise...Ch. 3 - Prob. 7PPCh. 3 - (Electrical eng.) a. The voltage gain of an...Ch. 3 - (Electrical eng.) a. Write, compile, and run a C++...Ch. 3 - (Electrical eng.) The amplification of electronic...Ch. 3 - (Acoustics) The loudness of a sound is measured in...Ch. 3 - (General math) a. A balance has the following...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- What is a functional decomposition diagram? what is a good example of a high level task being broken down into tasks in at least two lower levels (three levels in all).arrow_forwardWhat are the advantages to using a Sytems Analysis and Design model like the SDLC vs. other approaches?arrow_forward3. Problem Description: Define the Circle2D class that contains: Two double data fields named x and y that specify the center of the circle with get methods. • A data field radius with a get method. • A no-arg constructor that creates a default circle with (0, 0) for (x, y) and 1 for radius. • A constructor that creates a circle with the specified x, y, and radius. • A method getArea() that returns the area of the circle. • A method getPerimeter() that returns the perimeter of the circle. • • • A method contains(double x, double y) that returns true if the specified point (x, y) is inside this circle. See Figure (a). A method contains(Circle2D circle) that returns true if the specified circle is inside this circle. See Figure (b). A method overlaps (Circle2D circle) that returns true if the specified circle overlaps with this circle. See the figure below. р O со (a) (b) (c)< Figure (a) A point is inside the circle. (b) A circle is inside another circle. (c) A circle overlaps another…arrow_forward
- 1. Explain in detail with examples each of the following fundamental security design principles: economy of mechanism, fail-safe default, complete mediation, open design, separation of privilege, least privilege, least common mechanism, psychological acceptability, isolation, encapsulation, modularity, layering, and least astonishment.arrow_forwardSecurity in general means the protection of an asset. In the context of computer and network security, explore and explain what assets must be protected within an online university. What the threats are to the security of these assets, and what countermeasures are available to mitigate and protect the organization from such threats. For each of the assets you identify, assign an impact level (low, moderate, or high) for the loss of confidentiality, availability, and integrity. Justify your answers.arrow_forwardPlease include comments and docs comments on the program. The two other classes are Attraction and Entertainment.arrow_forward
- Object-Oriented Programming In this separate files. ent, you'll need to build and run a small Zoo in Lennoxville. All classes must be created in Animal (5) First, start by building a class that describes an Animal at a Zoo. It should have one private instance variable for the name of the animal, and one for its hunger status (fed or hungry). Add methods for setting and getting the hunger satus variable, along with a getter for the name. Consider how these should be named for code clarity. For instance, using a method called hungry () to make the animal hungry could be used as a setter for the hunger field. The same logic could be applied to when it's being fed: public void feed () { this.fed = true; Furthermore, the getter for the fed variable could be named is Fed as it is more descriptive about what it answers when compared to get Fed. Keep this technique in mind for future class designs. Zoo (10) Now we have the animals designed and ready for building a little Zoo! Build a class…arrow_forward1.[30 pts] Answer the following questions: a. [10 pts] Write a Boolean equation in sum-of-products canonical form for the truth table shown below: A B C Y 0 0 0 1 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 1 1 1 1 0 a. [10 pts] Minimize the Boolean equation you obtained in (a). b. [10 pts] Implement, using Logisim, the simplified logic circuit. Include an image of the circuit in your report. 2. [20 pts] Student A B will enjoy his picnic on sunny days that have no ants. He will also enjoy his picnic any day he sees a hummingbird, as well as on days where there are ants and ladybugs. a. Write a Boolean equation for his enjoyment (E) in terms of sun (S), ants (A), hummingbirds (H), and ladybugs (L). b. Implement in Logisim, the logic circuit of E function. Use the Circuit Analysis tool in Logisim to view the expression, include an image of the expression generated by Logisim in your report. 3.[20 pts] Find the minimum equivalent circuit for the one shown below (show your work): DAB C…arrow_forwardWhen using functions in python, it allows us tto create procedural abstractioons in our programs. What are 5 major benefits of using a procedural abstraction in python?arrow_forward
- Find the error, assume data is a string and all variables have been declared. for ch in data: if ch.isupper: num_upper = num_upper + 1 if ch.islower: num_lower = num_lower + 1 if ch.isdigit: num_digits = num_digits + 1 if ch.isspace: num_space = num_space + 1arrow_forwardFind the Error: date_string = input('Enter a date in the format mm/dd/yyyy: ') date_list = date_string.split('-') month_num = int(date_list[0]) day = date_list[1] year = date_list[2] month_name = month_list[month_num - 1] long_date = month_name + ' ' + day + ', ' + year print(long_date)arrow_forwardFind the Error: full_name = input ('Enter your full name: ') name = split(full_name) for string in name: print(string[0].upper(), sep='', end='') print('.', sep=' ', end='')arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
Programming Logic & Design ComprehensiveComputer ScienceISBN:9781337669405Author:FARRELLPublisher:Cengage
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks ColeNp Ms Office 365/Excel 2016 I NtermedComputer ScienceISBN:9781337508841Author:CareyPublisher:Cengage
C++ for Engineers and Scientists
Computer Science
ISBN:9781133187844
Author:Bronson, Gary J.
Publisher:Course Technology Ptr
C++ Programming: From Problem Analysis to Program...
Computer Science
ISBN:9781337102087
Author:D. S. Malik
Publisher:Cengage Learning
Programming Logic & Design Comprehensive
Computer Science
ISBN:9781337669405
Author:FARRELL
Publisher:Cengage
Operations Research : Applications and Algorithms
Computer Science
ISBN:9780534380588
Author:Wayne L. Winston
Publisher:Brooks Cole
Np Ms Office 365/Excel 2016 I Ntermed
Computer Science
ISBN:9781337508841
Author:Carey
Publisher:Cengage
Boolean Algebra - Digital Logic and Logic Families - Industrial Electronics; Author: Ekeeda;https://www.youtube.com/watch?v=u7XnJos-_Hs;License: Standard YouTube License, CC-BY
Boolean Algebra 1 – The Laws of Boolean Algebra; Author: Computer Science;https://www.youtube.com/watch?v=EPJf4owqwdA;License: Standard Youtube License