
Concept explainers
Two solid steel shafts (G = 77.2 GPa) are connected to a coupling disk B and to fixed supports at A and C. For the loading shown, determine (a) the reaction at each support, (a) the maximum shearing stress in shaft AB, (c) the maximum shearing stress in shaft BC.
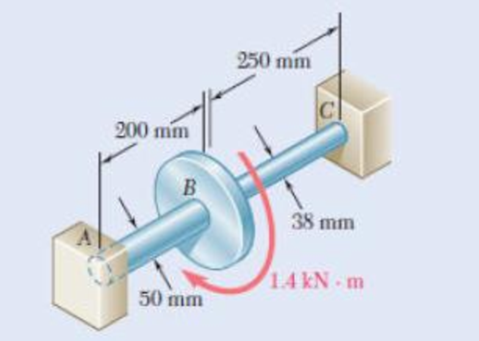
Fig. p3.55
(a)
The reaction at the supports.
Answer to Problem 55P
The reaction at the supports are
Explanation of Solution
Given information:
The modulus of rigidity of solid shafts is
Calculation:
The radius of the shaft AB is
The polar moment of inertia of shaft AB of radius
The torque carried by the shaft AB
Here,
Substitute
The radius of the shaft BC is
The polar moment of inertia of shaft BC of radius
The torque carried by the shaft BC
Here,
Substitute
The value of total torque in the shaft is
The total torque
Substitute
Substitute
Therefore, the reaction at the supports are
(b)
The maximum shearing stress in the shaft AB.
Answer to Problem 55P
The maximum shearing stress in the shaft AB is
Explanation of Solution
Given information:
The modulus of rigidity of solid shafts is
Calculation:
Refer (a).
The value of torque in the shaft AB is
The polar moment of inertia of shaft AB of radius
The maximum shearing stress in the shaft AB
Substitute
Therefore, the maximum shearing stress in the shaft AB is
(c)
The maximum shearing stress in the shaft BC.
Answer to Problem 55P
The maximum shearing stress in the shaft BC is
Explanation of Solution
Given information:
The modulus of rigidity of solid shafts is
Calculation:
Refer (a).
The value of torque in the shaft BC is
The polar moment of inertia of shaft BC of radius
The maximum shearing stress in the shaft BC
Substitute
Therefore, the maximum shearing stress in the shaft BC is
Want to see more full solutions like this?
Chapter 3 Solutions
EBK MECHANICS OF MATERIALS
- Explain why on the interval 0<x<1000 mm and 1000<x<2000mm, Mt is equal to positive 160 Nm, but at x= 0mm and x=1000mm Mt is equal to -160 Nm (negative value!). What is the reason for the sign change of Mt?arrow_forward20 3. 2-233 2520 Тр Gears 1079 A pair of helical gears consist of a 20 teeth pinion meshing with a 100 teeth gear. The pinion rotates at Ta 720 r.p.m. The normal pressure angle is 20° while the helix angle is 25°. The face width is 40 mm and the normal module is 4 mm. The pinion as well as gear are made of steel having ultimate strength of 600 MPa and heat treated to a surface hardness of 300 B.H.N. The service factor and factor of safety are 1.5 and 2 respectively. Assume that the velocity factor accounts for the dynamic load and calculate the power transmitting capacity of the gears. [Ans. 8.6 kWarrow_forward4. A single stage helical gear reducer is to receive power from a 1440 r.p.m., 25 kW induction motor. The gear tooth profile is involute full depth with 20° normal pressure angle. The helix angle is 23°, number of teeth on pinion is 20 and the gear ratio is 3. Both the gears are made of steel with allowable beam stress of 90 MPa and hardness 250 B.H.N. (a) Design the gears for 20% overload carrying capacity from standpoint of bending strength and wear, (b) If the incremental dynamic load of 8 kN is estimated in tangential plane, what will be the safe power transmitted by the pair at the same speed?arrow_forward
- Determine the stress in each section of the bar shown in Fig. when subjected to an axial tensile load shown in Fig. The central section is 30 mm hollow square cross- section; the other portions are of circular section, their diameters being indicated What will be the total deformation of the bar? For the bar material E = 210GPa. 20mi О 30mm 30mmm 2.6 15mm 30kN 1 2 10kN - 20kN 3 -329 91mm 100mm 371mmarrow_forwardCalculate the load that will make point A move to the left by 6mm, E=228GPa. The diameters of the rods are as shown in fig. below. 2P- PA 80mm B 200mm 2P 0.9m 1.3m.arrow_forwardIf the rods are made from a square section with the dimension as shown. Calculate the load that will make point A move to the left by 6mm, E=228GPa. 2P- P A 80mm B 200mm 2P 0.9m 1.3marrow_forward
- 3. 9. 10. The centrifugal tension in belts (a) increases power transmitted (b) decreases power transmitted (c) have no effect on the power transmitted (d) increases power transmitted upto a certain speed and then decreases When the belt is stationary, it is subjected to some tension, known as initial tension. The value of this tension is equal to the (a) tension in the tight side of the belt (b) tension in the slack side of the belt (c) sum of the tensions in the tight side and slack side of the belt (d) average tension of the tight side and slack side of the belt The relation between the pitch of the chain (p) and pitch circle diameter of the sprocket (d) is given by 60° (a) p=d sin (c) p=d sin (120° T where T Number of teeth on the sprocket. 90° (b) p=d sin T 180° (d) p=d sin Tarrow_forwardOBJECTIVE TYPE QUESTIONS 1. The maximum fluctuation of energy is the 2. (a) sum of maximum and minimum energies (b) difference between the maximum and minimum energies (c) ratio of the maximum energy and minimum energy (d) ratio of the mean resisting torque to the work done per cycle In a turning moment diagram, the variations of energy above and below the mean resisting torque line is called (a) fluctuation of energy (b) maximum fluctuation of energy (c) coefficient of fluctuation of energy (d) none of the above Chapter 16: Turning Moment Diagrams and Flywheel 611 The ratio of the maximum fluctuation of speed to the mean speed is called 3. (a) fluctuation of speed (c) coefficient of fluctuation of speed 4. (b) maximum fluctuation of speed (a) none of these The ratio of the maximum fluctuation of energy to the.......... is called coefficient of fluctuation of energy. (a) minimum fluctuation of energy (b) work done per cycle The maximum fluctuation of energy in a flywheel is equal to 5.…arrow_forwardOBJECTIVE TYPE QUESTIONS 1. The velocity ratio of two pulleys connected by an open belt or crossed belt is 2. (a) directly proportional to their diameters (b) inversely proportional to their diameters (c) directly proportional to the square of their diameters (d) inversely proportional to the square of their diameters Two pulleys of diameters d, and d, and at distance x apart are connected by means of an open belt drive. The length of the belt is (a)(d+d₁)+2x+ (d₁+d₂)² 4x (b)(d₁-d₂)+2x+ (d₁-d₂)² 4x (c)(d₁+d₂)+ +2x+ (d₁-d₂)² 4x (d)(d-d₂)+2x+ (d₁ +d₂)² 4x 3. In a cone pulley, if the sum of radii of the pulleys on the driving and driven shafts is constant, then (a) open belt drive is recommended (b) cross belt drive is recommended (c) both open belt drive and cross belt drive are recommended (d) the drive is recommended depending upon the torque transmitted Due to slip of the belt, the velocity ratio of the belt drive 4. (a) decreases 5. (b) increases (c) does not change When two pulleys…arrow_forward
- Q3: (10 MARKS) A piston with a weight of 29.4 N is supported by a spring and dashpot. A dashpot of damping coefficient c = 275 N.s/m acts in parallel with the spring of stiffness k = 2400 N/m. A fluctuating pressure p = 960 sin 30t N/m² acts on the piston, whose top surface area is 0.05 m². Determine the steady-state displacement as a function of time and the maximum force transmitted to the base. P=Po sin cot Warrow_forward9. Design a spur gear drive required to transmit 45 kW at a pinion speed of 800 r.p.m. The velocity ratio is 3.5 : 1. The teeth are 20° full-depth involute with 18 teeth on the pinion. Both the pinion and gear are made of steel with a maximum safe static stress of 180 MPa. Assume a safe stress of 40 MPa for the material of the shaft and key. 10. Design a pair of spur gears with stub teeth to transmit 55 kW from a 175 mm pinion running at 2500 r.p.m. to a gear running at 1500 r.p.m. Both the gears are made of steel having B.H.N. 260. Approximate the pitch by means of Lewis equation and then adjust the dimensions to keep within the limits set by the dynamic load and wear equation.arrow_forward7. A motor shaft rotating at 1440 r.p.m. has to transmit 15 kW to a low speed shaft rotating at 500 r.p.m. The teeth are 20° involute with 25 teeth on the pinion. Both the pinion and gear are made of cast iron with a maximum safe stress of 56 MPa. A safe stress of 35 MPa may be taken for the shaft on which the gear is mounted. Design and sketch the spur gear drive to suit the above conditions. The starting torque may be assumed as 1,25 times the running torque. Ruins 20 LW at 100 nm to another shaft running approxiarrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





