
Figure 31-19 shows three oscillating LC circuits with identical inductors and capacitors At a particular time, the charges on the capacitor plates (and thus the electric fields between the plates) are all at their maximum values Rank the circuits according to the time taken to fully discharge the capacitors during the oscillations, greatest first.
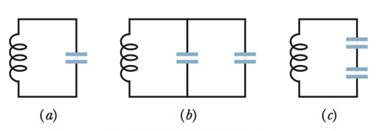
Figure 31-19 Question 1.
To find:
The rank of the circuits according to the time taken to fully discharge the capacitors during the oscillations.
Answer to Problem 1Q
Solution:
The rank of the circuits according to time taken to fully discharge the capacitors during the oscillations is circuit b, circuit a, circuit c.
Explanation of Solution
1) Concept:
The charging and discharging of a capacitor in a LC circuit is like an oscillatory motion. The period of these oscillations depends upon the values of the inductance and the capacitance in the circuit.
2) Formula:
i)
ii)
3) Given:
i) The inductors and capacitors in the three circuits are identical.
ii) The two capacitors in the circuit b are in parallel combination.
iii) The two capacitors in the circuit c are in series combination.
4) Calculations:
a) Consider circuit b. The two capacitors are connected in parallel combination. Hence the effective capacitance of the circuit is
Since both the capacitors are identical, the effective capacitance is
b) Now, consider circuit c. The two capacitors are connected in series combination. Hence the effective capacitance of the circuit is
Since both the capacitors are identical, the effective capacitance is
c) The period of oscillations is calculated using the equation
and
i.e.,
Thus, we see that
But since the inductors in the three circuits are identical,
Now, for circuit b, the effective capacitance is greatest among the three. Hence its period is also the greatest. Thus, time for the capacitor to discharge fully, which is
For circuit a, the capacitance is C, which is smaller than that for circuit b. Hence the time for the discharge will also be smaller.
For circuit c, the effective capacitance is the smallest among the three. Hence the time required for complete discharge will also be the smallest.
Thus the ranks for the circuits are circuit b, circuit a, and then circuit c.
Conclusion:
The time required for the capacitor to discharge fully is
Want to see more full solutions like this?
Chapter 31 Solutions
Fundamentals of Physics Extended
Additional Science Textbook Solutions
College Physics: A Strategic Approach (3rd Edition)
Human Biology: Concepts and Current Issues (8th Edition)
Microbiology with Diseases by Body System (5th Edition)
Fundamentals Of Thermodynamics
Genetic Analysis: An Integrated Approach (3rd Edition)
Introductory Chemistry (6th Edition)
- pls help on all asked questions kindlyarrow_forward19. Mount Everest, Earth's highest mountain above sea level, has a peak of 8849 m above sea level. Assume that sea level defines the height of Earth's surface. (re = 6.38 × 106 m, ME = 5.98 × 1024 kg, G = 6.67 × 10 -11 Nm²/kg²) a. Calculate the strength of Earth's gravitational field at a point at the peak of Mount Everest. b. What is the ratio of the strength of Earth's gravitational field at a point 644416m below the surface of the Earth to a point at the top of Mount Everest? C. A tourist watching the sunrise on top of Mount Everest observes a satellite orbiting Earth at an altitude 3580 km above his position. Determine the speed of the satellite.arrow_forwardpls help on allarrow_forward
- pls help on allarrow_forward6. As the distance between two charges decreases, the magnitude of the electric potential energy of the two-charge system: a) Always increases b) Always decreases c) Increases if the charges have the same sign, decreases if they have the opposite signs d) Increases if the charges have the opposite sign, decreases if they have the same sign 7. To analyze the motion of an elastic collision between two charged particles we use conservation of & a) Energy, Velocity b) Momentum, Force c) Mass, Momentum d) Energy, Momentum e) Kinetic Energy, Potential Energyarrow_forwardpls help on all asked questions kindlyarrow_forward
- pls help on all asked questions kindlyarrow_forward17. Two charges, one of charge +2.5 × 10-5 C and the other of charge +3.7 × 10-6 C, are 25.0 cm apart. The +2.5 × 10−5 C charge is to the left of the +3.7 × 10−6 C charge. a. Draw a diagram showing the point charges and label a point Y that is 20.0 cm to the left of the +3.7 × 10-6 C charge, on the line connecting the charges. (Field lines do not need to be drawn.) b. Calculate the net electric field at point Y.arrow_forward3arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





