Chapter 31, Problem 15P

(a)

To determine

The current in inductor.

Answer to Problem 15P

The current in inductor in the term of time is $0.500\left(1-e^{-10.0t}\right)$.

Explanation of Solution

Given info: value of resistance $R$ is $4.00\Omega$, inductance of the circuit is $1.00\text{H}$ and emf of the battery is $10.0\text{V}$.

Diagram for the circuit connected with a battery, inductor is given below.

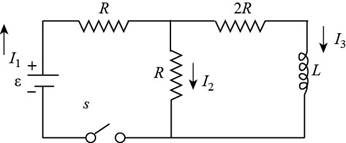
Figure (1)

Formula to calculate current in a loop as per Kirchhoff law is,

$\begin{array}{c}{\displaystyle \sum i}=0\\ I_s-I-I_L=0\\ I=I_s-I_L\end{array}$ (1)

Here,

$I_s$ is current flowing through switch $\text{s}$.

$I$ is current flowing through resistance $\text{R}$.

$I_l$ is the current flowing through the inductance $L$.

Write the expression for net voltage in loop 1,

$\epsilon -R{I}_s-RI=0$ (2)

Write the expression to calculate net voltage in loop 2,

$\epsilon -R{I}_s-2R{I}_L-L\frac{d{I}_L}{dt}=0$ (3)

Here,

$R$ is resistance of circuit.

$L$ is inductance of circuit.

$\frac{d{I}_L}{dt}$ is the rate of change of current in inductance.

Substitute $I_s-I_L$ for $I$ in equation (2).

$\begin{array}{c}\epsilon -R{I}_s-R\left(I_s-I_L\right)=0\\ \epsilon -2R{I}_s-R{I}_L=0\\ I_{\text{s}}=\frac{\epsilon }{2R}+\frac{I_L}{2}\end{array}$ (4)

Substitute $\frac{\epsilon }{2R}+\frac{I_L}{2}$ for $I_s$ in equation (3).

$\begin{array}{l}\epsilon -R\left(\frac{\epsilon }{2R}+\frac{I_L}{2}\right)-2R{I}_L-L\frac{d{I}_L}{dt}=0\\ \epsilon -\left(\frac{\epsilon }{2}+\frac{R{I}_L}{2}\right)-2R{I}_L-L\frac{d{I}_L}{dt}=0\\ \frac{\epsilon }{2}-\frac{R{I}_L}{2}-2R{I}_L-L\frac{d{I}_L}{dt}=0\\ \frac{\epsilon }{2}-\frac{5R{I}_L}{2}-L\frac{d{I}_L}{dt}=0\end{array}$

Arrange the terms of above equation to simplify for integration.

$\begin{array}{l}L\frac{d{I}_L}{dt}=\frac{\epsilon }{2}-2.5R{I}_L\\ \frac{L}{2.5R}\frac{d{I}_L}{dt}=\frac{\epsilon }{5R}-I_L\\ -\frac{L}{2.5R}\frac{d{I}_L}{dt}=\left(-\frac{\epsilon }{5R}+I_L\right)\\ \frac{d{I}_L}{\left(-\frac{\epsilon }{5R}+I_L\right)}=-\frac{2.5R}{L}dt\end{array}$

On integrate,

${\displaystyle \int \frac{d{I}_L}{-\frac{\epsilon }{5R}+I_L}}={\displaystyle \int \left(-\frac{2.5R}{L}\right)}dt$ (5)

Let $-\frac{\epsilon }{5R}+I_L=T$.

Differentiate above equation.

$d{I}_L=dT$

Substitute $dT$ for $d{I}_L$ and $T$ for $-\frac{\epsilon }{5R}+I_L$ in equation (5).

$\begin{array}{l}{\displaystyle \int \frac{d{I}_L}{T}}={\displaystyle \int \left(-\frac{2.5R}{L}\right)}dt\\ {\displaystyle \int \frac{d{I}_L}{T}}=-\frac{2.5R}{L}{\displaystyle \int dt}\\ \ln T=-\frac{2.5R}{L}t+c\end{array}$

Substitute $-\frac{\epsilon }{5R}+I_L$ for $T$ in above equation.

$\ln \left(-\frac{\epsilon }{5R}+I_L\right)=-\frac{2.5R}{L}t+c$ (6)

Apply boundary condition,

Substitute $0$ for $t$ and $0$ for $I_L$ in above equation.

$\begin{array}{c}\ln \left(-\frac{\epsilon }{5R}+0\right)=-\frac{2.5R}{L}\times 0+c\\ c=\ln \left(-\frac{\epsilon }{5R}\right)\end{array}$

Substitute $\ln \left(-\frac{\epsilon }{5R}\right)$ for $c$ in equation (VI)

$\begin{array}{l}\ln \left(-\frac{\epsilon }{5R}+I_L\right)=-\frac{2.5R}{L}t+\ln \left(-\frac{\epsilon }{5R}\right)\\ \ln \left(-\frac{\epsilon }{5R}+I_L\right)-\ln \left(-\frac{\epsilon }{5R}\right)=-\frac{2.5R}{L}t\\ \ln \frac{\left(-\frac{\epsilon }{5R}+I_L\right)}{\left(-\frac{\epsilon }{5R}\right)}=-\frac{2.5R}{L}t\\ \end{array}$

Further solve the above expression.

$\begin{array}{l}\ln \left(1-\frac{I_L}{\frac{\epsilon }{5R}}\right)=-\frac{2.5R}{L}t\\ 1-\frac{I_L}{\frac{\epsilon }{5R}}=e^{-\frac{2.5R}{L}t}\\ I_L=\frac{\epsilon }{5R}\left(1-e^{-\frac{2.5R}{L}t}\right)\end{array}$

Substitute $10\text{V}$ for $\epsilon$, $4\text{}\Omega$ for $R$ and $1\text{H}$ for $L$ in above equation.

$\begin{array}{c}{I}_L=\frac{10.0\text{V}}{5\left(4\Omega \right)}\left(1-e^{-\frac{2.5\times 4\Omega }{1\text{H}}t}\right)\\ =0.500\left(1-e^{-10.0t}\right)\end{array}$ (7)

Thus, the current in inductor in the terms of time is $0.500\left(1-e^{10.0t}\right)$.

Conclusion:

Therefore, current in inductor in the terms of time is $0.500\left(1-e^{10.0t}\right)$.

(b)

To determine

The current in the switch as a function of time.

Answer to Problem 15P

The current in the switch as the function of time is $1.50-0.25e^{-10.0t}$.

Explanation of Solution

From equation (7), the formula to calculate current in inductor is,

$I_L=0.5\left(1-e^{-10.0t}\right)$

From equation (4), the formula to calculate current in switch is,

$I_{\text{s}}=\frac{\epsilon }{2R}+\frac{I_L}{2}$

Substitute $0.5\left(1-e^{-10.0t}\right)$ for $I_L$ in above equation to calculate $I_{\text{s}}$.

$\begin{array}{c}{I}_{\text{s}}=\frac{\epsilon }{2R}+\frac{1}{2}\left(0.5\left(1-e^{-10.0t}\right)\right)\\ =\frac{\epsilon }{2R}+0.25\left(1-e^{-10.0t}\right)\end{array}$

Substitute $10\text{V}$ for $\epsilon$ and $4.0\Omega$ for $r$ in above equation.

$\begin{array}{c}{I}_{\text{s}}=\frac{10\text{V}}{2\left(4\Omega \right)}+0.25\left(1-e^{-10.0t}\right)\\ =1.25+0.25\left(1-e^{-10.0t}\right)\\ =1.50-0.25e^{-10.0t}\end{array}$

Thus, the current in switch is $1.50-0.25e^{-10.0t}$.

Conclusion:

Therefore, the current in switch is $1.50-0.25e^{-10.0t}$.