Chapter 3, Problem 59E

(a)

To determine

Find current through $1\text{k}\Omega$ resistor in the circuit.

Answer to Problem 59E

The current through $1\text{k}\Omega$ resistor in the circuit is $-10.9\text{cos1000}t\mu \text{A}$.

Explanation of Solution

Given data:

Value of trans-conductance $g_m$ is $1.2\text{mS}$ and

Value of voltage supply $v_s$ is $12\cos 1000t\text{mV}$.

Calculation:

The redrawn circuit is shown in Figure 1.

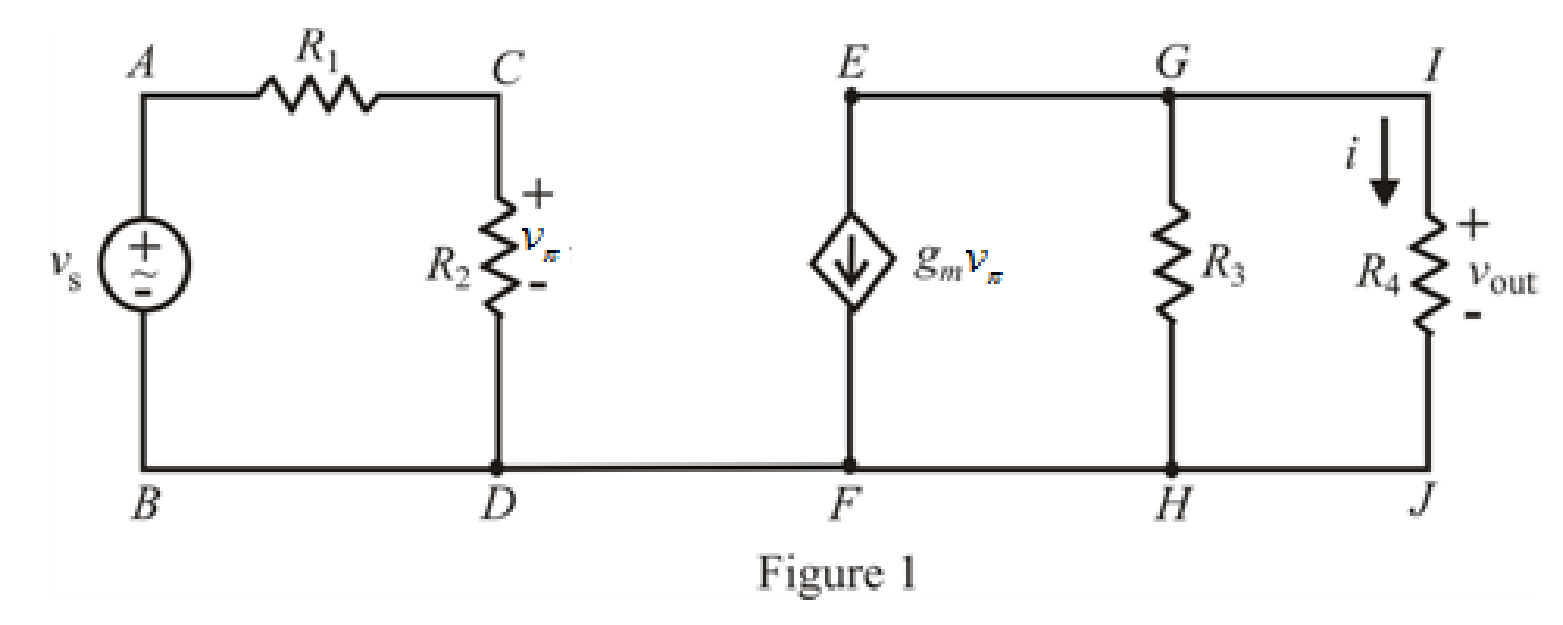
Refer to the Figure 1.

The expression for voltage division across resistance $R_2$ is,

$v_{\pi }=v_s\times \left(\frac{R_2}{R_1+R_2}\right)$ (1)

Here,

$v_{\pi }$ is the voltage across resistance $R_2$,

$R_2$ is the resistance across branch $CD$,

$v_s$ is the supply voltage and

$R_1$ is the resistance across branch $AC$.

The expression for current division rule across resistance $R_4$ is,

$i=\left(-g_m{v}_{\pi }\right)\times \left(\frac{R_3}{R_3+R_4}\right)$ (2)

Here,

$i$ is the current flowing from $R_4$ resistance across branch $IJ$,

$-g_m{v}_{\pi }$ is the current dependent source flowing opposite across branch $EF$,

$R_3$ is the resistance across branch $GH$ and

$R_4$ is the resistance across branch $IJ$.

Substitute $12\text{cos1000}t\text{mV}$ for $v_s$, $3\text{k}\Omega$ for $R_1$, $15\text{k}\Omega$ for $R_2$ in the equation (1).

$\begin{array}{c}{v}_{\pi }=12\text{cos1000}t\text{mV}\times \left(\frac{15\text{k}\Omega }{3\text{ k}\Omega \text{+15}\text{k}\Omega }\right)\\ =12\times {10}^{-3}\text{cos1000}t\text{V}\times \left(\frac{15\times {10}^3\Omega }{3\times {10}^3\Omega \text{+15}\times {\text{10}}^3\Omega }\right)\left\{\begin{array}{l}\because \text{ 1}\text{k}\Omega =\text{1}\times {\text{10}}^3\Omega \\ \because 1\text{mV}=\text{1}\times {\text{10}}^{-3}\text{V}\end{array}\right\}\\ =12\times {10}^{-3}\text{cos1000}t\text{ V}\times \left(\frac{15\times {10}^3\Omega }{18\times {10}^3\Omega }\right)\end{array}$

Solve for $v_{\pi }$.

$\begin{array}{c}{v}_{\pi }\text{=10}\times {\text{10}}^{-3}\text{cos1000}t\text{V}\\ {\text{=10}}^{-2}\text{cos1000}t\text{V}\end{array}$

Substitute ${\text{10}}^{-2}\text{cos1000}t\text{V}$ for $v_{\pi }$, $1.2\text{mS}$ for $g_m$, $10\text{k}\Omega$ for $R_3$ and $1\text{k}\Omega$ for $R_4$ in the equation (2).

$\begin{array}{c}i=\left(-1.2\text{mS}\times {\text{10}}^{-2}\text{cos1000}t\text{V}\right)\times \left(\frac{10\text{k}\Omega }{10\text{k}\Omega +1\text{k}\Omega }\right)\\ =\left(-1.2\times {10}^{-3}\text{S}\times {\text{10}}^{-2}\text{cos1000}t\text{V}\right)\times \left(\frac{10\times {10}^3\Omega }{10\times {10}^3\Omega +1\times {10}^3\Omega }\right)\left\{\begin{array}{l}\because \text{1}\text{k}\Omega =\text{1}\times {\text{10}}^3\Omega \\ \because 1\text{mV}=\text{1}\times {\text{10}}^{-3}\text{V}\end{array}\right\}\\ =\left(-1.2\times {10}^{-3}\text{ S}\times {\text{10}}^{-2}\text{cos1000}t\text{V}\right)\times \left(0.909\right)\end{array}$

Solve for $i$.

$\begin{array}{c}i=\left(-1.09\text{cos1000}t\times {10}^{-5}\text{A}\right)\\ =-10.9\text{cos1000}t\times {\text{10}}^{-6}\text{A}\end{array}$

$i=-10.9\text{cos1000}t\mu \text{A}\left\{\because 1\mu \text{A}=\text{1}\times {\text{10}}^{-6}\text{A}\right\}$ (3)

Conclusion:

Thus, the current across the $1\text{k}\Omega$ resistance  in the circuit is $-10.9\text{cos1000}t\mu \text{A}$.

(b)

To determine

Find the amplifier output voltage $v_{\text{out}}$ in the given circuit.

Answer to Problem 59E

The amplifier output voltage $v_{\text{out}}$ is $-10.9\text{cos1000}t\text{mV}$.

Explanation of Solution

Calculation:

Refer to the Figure 1.

The expression for ohm’s law across resistance $R_4$ is,

$v_{\text{out}}=\left(i\times R_4\right)$ (4)

Here,

$v_{\text{out}}$ is the amplifier voltage output and

$R_4$ is the resistance across branch $IJ$.

Refer to the Figure 1.

Substitute $-10.9\text{cos1000}t\mu \text{A}$ for $i$ and $1\text{k}\Omega$ for $R_4$ in the equation (5).

$\begin{array}{c}{v}_{\text{out}}=\left(-10.9\text{cos1000}t\mu \text{A}\times \text{1}\text{k}\Omega \right)\\ =\left(-10.9\text{cos1000}t\times {10}^{-6}\text{A}\times 1\times {10}^3\Omega \right)\left\{\because \text{ 1 }\mu \text{A}={\text{10}}^{-6}\text{ A, 1 k}\Omega ={\text{10}}^3\Omega \right\}\\ =-10.9\text{cos1000}t\times {10}^{-3}\text{V}\end{array}$

$v_{\text{out}}=-10.9\text{cos1000}t\text{mV}\left\{\because \text{1 V}=\text{1}\times {\text{10}}^3\text{mV}\right\}$ (5)

Conclusion:

Thus, the amplifier output voltage in the circuit is $-10.9\text{cos1000}t\text{mV}$.

(c)

To determine

Check whether the circuit can amplify the signal.

Answer to Problem 59E

The amplified output voltage can’t amplify the input signal because $v_{out}$ is not greater than $v_s$.

Explanation of Solution

Refer to Figure 1

The amplified output voltage $v_{out}$$-10.9\text{cos1000}t\text{mV}$ is calculated in the equation (5). The input sinusoidal voltage across the circuit is $12\text{cos1000}t\mu \text{V}$.

For the amplification, the desired condition must satisfy which is $v_{out}>v_s$. While from the equation (5) it is clear that $v_{out}$ is not greater than $v_s$.

Conclusion:

Thus, the amplified output voltage can’t amplify the input signal because $v_{out}$ is not greater than $v_s$.

(d)

To determine

Check whether the circuit can amplify the signal for input voltage $v_{\pi }$.

Answer to Problem 59E

The circuit can amplify the input signal because it satisfies the condition $v_{out}>v_{\pi }$.

Explanation of Solution

Refer to Figure 1

The amplified output voltage $v_{out}$ is $-10.9\text{cos1000}t\text{mV}$ calculated in the equation (5). The input sinusoidal voltage across the circuit is taken as $v_{\pi }$ which is equal to $10\text{cos1000}t\text{mV}$.

For the amplification, the desired condition must satisfy which is $v_{out}>v_s$. And from the equation (5) it is clear that $v_{out}$ is greater than $v_s$.

Conclusion:

Thus, circuit can amplify the input signal because it satisfies the condition $v_{out}>v_{\pi }$.