Problem 3.1CYU: Check Your Understanding In the system used in the preceding examples, at what angles are the first... Problem 3.2CYU: Check Your Understanding Going further with Example 3.4, what are the next two thicknesses of soap... Problem 3.3CYU: Check Your Understanding Although m, the number of fringes observed, is an integer, which is often... Problem 1CQ: Young’s double-slit experiment breaks a single light beam into two sources. Would the same pattern... Problem 2CQ: Is it possible to create a experimental setup in which there is only destructive interference?... Problem 3CQ: Why won’t two small sodium lamps, held close together, produce an interference pattern on a distant... Problem 4CQ: Suppose you use the same double slit to perform Young’s double-slit experiment in air and then... Problem 5CQ: Why is monochromatic light used in the double slit experiment? What would happen if white light were... Problem 6CQ: What effect does increasing the wedge angle have on the spacing of interference fringes? If the... Problem 7CQ: How is the difference in paths taken by two originally in-phase light waves related to whether they... Problem 8CQ: Is there a phase change in the light reflected from either surface of a contact lens floating on a... Problem 9CQ: In placing a sample on a microscope slide, a glass cover is placed over a water drop on the glass... Problem 10CQ: Answer the above question if the fluid between the two pieces of crown glass is carbon disulfide. Problem 11CQ: While contemplating the food value of a slice of ham, you notice a rainbow of color reflected from... Problem 12CQ: An inventor notices that a soap bubble is dark at its thinnest and realizes that destructive... Problem 13CQ: A nonreflective coating like the one described in Example 3.3 works ideally for a single wavelength... Problem 14CQ: Why is it much more difficult to see interference fringes for light reflected from a thick piece of... Problem 15CQ: Describe how a Michelson interferometer can be used to measure the index of refraction of a gas... Problem 16P: At what angle is the first-order maximum for 450-nm wavelength blue light falling on double slits... Problem 17P: Calculate the angle for the third-order maximum of 580-nm wavelength yellow light falling on double... Problem 18P: What is the separation between two slits for which 610-nm orange light has its first maximum at an... Problem 19P: Find the distance between two slits that produces the first minimum for 410-nm violet light at an... Problem 20P: Calculate the wavelength of light that has its third minimum at an angle of 30.0° when falling on... Problem 21P: What is the wavelength of light falling on double slits separated by 2.00 m if the third-order... Problem 22P: At what angle is the fourth-order maximum for the situation in the preceding problem? Problem 23P: What is the highest-order maximum for 400-nm light falling on double slits separated by 25.0 m? Problem 24P: Find the largest wavelength of light falling on double slits separated by 1.20 m for which there is... Problem 25P: What is the smallest separation between two slits that will produce a second-order maximum for... Problem 26P: (a) What is the smallest separation between two slits that will produce a second-order maximum for... Problem 27P: (a) If the first-order maximum for monochromatic light falling on a double slit is at an angle of... Problem 28P: Shown below is a double slit located a distance x from a screen, with the distance from the center... Problem 29P: Using the result of the preceding problem, (a) calculate the distance between fringes for 633-nm... Problem 30P: Using the result of the problem two problems prior, find the wavelength of light that produces... Problem 31P: In a double-slit experiment, the fifth maximum is 2.8 cm from the central maximum on a screen that... Problem 32P: The source in Young’s experiment emits at two wavelengths. On the viewing screen, the fourth maximum... Problem 33P: If 500-nm and 650-nm light illuminates two slits that are separated by 0.50 mm, how far apart are... Problem 34P: Red light of wavelength of 700 nm falls on a double slit separated by 400 nm. (a) At what angle is... Problem 35P: Ten narrow slits are equally spaced 0.25 mm apart and illuminated with yellow light of wavelength... Problem 36P: The width of bright fringes can be calculated as the separation between the two adjacent dark... Problem 37P: For a three-slit interference pattern, find the ratio of the peak intensities of a secondary maximum... Problem 38P: What is the angular width of the central fringe of the interference pattern of (a) 20 slits... Problem 39P: A soap bubble is 100 nm thick and illuminated by white light incident perpendicular to its surface.... Problem 40P: An oil slick on water is 120 nm thick and illuminated by white light incident perpendicular to its... Problem 41P: Calculate the minimum thickness of an oil slick on water that appears blue when illuminated by white... Problem 42P: Find the minimum thickness of a soap bubble that appears red when illuminated by white light... Problem 43P: A film of soapy water (n=1.33) on top of a plastic cutting board has a thickness of 233 nm. What... Problem 44P: What are the three smallest non-zero thicknesses of soapy water (n=1.33) on Plexiglas if it appears... Problem 45P: Suppose you have a lens system that is to be used primarily for 700-nm red light. What is the second... Problem 46P: (a) As a soap bubble thins it becomes dark, because the path length difference becomes small... Problem 47P: To save money on making military aircraft invisible to radar, an inventor decides to coat them with... Problem 48P: A Michelson interferometer has two equal arms. A mercury light of wavelength 546 nm is used for the... Problem 49P: What is the distance moved by the traveling mirror of a Michelson interferometer that corresponds to... Problem 50P: When the traveling mirror of a Michelson interferometer is moved 2.40105 m, 90 fringes pass by a... Problem 51P: In a Michelson interferometer, light of wavelength 632.8 nm from a He-Ne laser is used. When one of... Problem 52P: A chamber 5.0 cm long with flat, parallel windows at the ends is placed in one arm of a Michelson... Problem 53AP: For 600-nm wavelength light and a slit separation of 0.12 mm, what are the angular positions of the... Problem 54AP: If the light source in the preceding problem is changed, the angular position of the third maximum... Problem 55AP: Red light (=710.nm) illuminates double slits separated by a distance d=0.150 mm. The screen and the... Problem 56AP: Two sources as in phase and emit waves with =0.42 m. Determine whether constructive or destructive... Problem 57AP: Two slits 4.0106 m apart are illuminated by light of wavelength 600 nm. What is the highest order... Problem 58AP: Suppose that the highest order fringe that can be observed is the eighth in a double-slit experiment... Problem 59AP: The interference pattern of a He-Ne laser light (=632.9nm) passing through two slits 0.031 mm apart... Problem 60AP: Young’s double-slit experiment is performed immersed in water (n=1.333) . The light source is a... Problem 61AP: A double-slit experiment is to be set up so that the bright fringes appear 1.27 cm apart on a screen... Problem 62AP: An effect analogous to two-slit interference can occur with sound waves, instead of light. In an... Problem 63AP: A hydrogen gas discharge lamp emits visible light at four wavelengths, =410 , 434, 486, and 656 nm.... Problem 64AP: Monochromatic light of frequency 5.51014 Hz falls on 10 slits separated by 0.020 mm. What is the... Problem 65AP: Eight slits equally separated by 0.149 mm is uniformly illuminated by a monochromatic light at =523... Problem 66AP: Eight slits equally separated by 0.149 mm is uniformly illuminated by a monochromatic light at =523... Problem 67AP: A transparent film of thickness 250 nm and index of refraction of 1.40 is surrounded by air. What... Problem 68AP: An intensity minimum is found for 450 nm light transmitted through a transparent film (n=1.20) in... Problem 69AP: A thin film with n=1.32 is surrounded by air. What is the minimum thickness of this film such that... Problem 70AP: Repeat your calculation of the previous problem with the thin film placed on a flat glass (n=1.50)... Problem 71AP: After a minor oil spill, a think film of oil (n=1.40) of thickness 450 nm floats on the water... Problem 72AP: A microscope slide 10 cm long is separated from a glass plate at one end by a sheet of paper. As... Problem 73AP: Suppose that the setup of the preceding problem is immersed in an unknown liquid. If 18 fringes per... Problem 74AP: A thin wedge filled with air is produced when two flat glass plates are placed on top of one another... Problem 75AP: Two identical pieces of rectangular plate glass are used to measure the thickness of a hair. The... Problem 76AP: Two microscope slides made of glass are illuminated by monochromatic (=589nm) light incident... Problem 77AP: A good quality camera “lens” is actually a system of lenses, rather than a single lens, but a side... Problem 78AP: Constructive interference is observed from directly above an oil slick for wavelengths (in air) 440... Problem 79AP: A soap bubble is blown outdoors. What colors (indicate by wavelengths) of the reflected sunlight are... Problem 80AP: A Michelson interferometer with a He-Ne laser light source (=632.8nm) projects its interference... Problem 81AP: An experimenter detects 251 fringes when the movable mirror in a Michelson interferometer is... Problem 82AP: A Michelson interferometer is used to measure the wavelength of light put through it. When the... Problem 83AP: A 5.08-cm-long rectangular glass chamber is inserted into one arm of a Michelson interferometer... Problem 84AP: Into one arm of a Michelson interferometer, a plastic sheet of thickness 75 m is inserted, which... Problem 85AP: The thickness of an aluminum foil is measured using a Michelson interferometer that has its movable... Problem 86AP: The movable mirror of a Michelson interferometer is attached to one end of a thin metal rod of... Problem 87AP: In a thermally stabilized lab, a Michelson interferometer is used to monitor the temperature to... Problem 88AP: A 65-fringe shift results in a Michelson interferometer when a 42.0-µm film made of an unknown... Problem 89CP: Determine what happens to the double-slit interference pattern if one of the slits is covered with a... Problem 90CP: Fifty-one narrow slits are equally spaced and separated by 0.10 mm. The slits are illuminated by... Problem 91CP: A film of oil on water will appear dark when it is very thin, because the path length difference... Problem 92CP: Figure 3.14 shows two glass slides illuminated by monochromatic light incident perpendicularly. The... Problem 93CP: Figure 3.14 shows two 7.50-cm-long glass slides illuminated by pure 589-nm wavelength light incident... Problem 94CP: A soap bubble is 100 nm thick and illuminated by white light incident at a 45° angle to its surface.... Problem 95CP: An oil slick on water is 120 nm thick and illuminated by white light incident at a 45° angle to its... format_list_bulleted

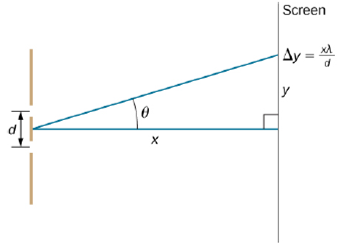

 University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning




