Chapter 28, Problem 7P

The following equations define the concentrations of threereactants:

$\begin{array}{l}\frac{d{c}_a}{dt}=-10c_a{c}_c+c_b\\ \frac{d{c}_b}{dt}=-10c_a{c}_c-c_b\\ \frac{d{c}_c}{dt}=-10c_a{c}_c+c_b-2c_c\end{array}$

If the initial conditions are $c_a=50,c_b=0,\text{ and }{c}_c=40$, find the concentrations for the times from 0 to 3 s.

To determine

To calculate: The concentration for the times from $0\text{ to }3\text{ s}$. Where the equations for concentrations of three reactants are,

$\begin{array}{c}\frac{d{c}_a}{dt}=-10c_a{c}_c+c_b\\ \frac{d{c}_b}{dt}=10c_a{c}_c-c_b\\ \frac{d{c}_c}{dt}=-10c_a{c}_c+c_b-2c_c\end{array}$

Initials conditions are $c_a=50,c_b=0\text{ and }{c}_c=40$

Answer to Problem 7P

Solution:

The concentration of the reactants $c_a,c_b\text{ and }{c}_c$ at $t=0\text{ s}$ are $50,0,40$ respectively.

The concentration of the reactants $c_a,c_b\text{ and }{c}_c$ at $t=1\text{ s}$ are $50,0,5.4135$ respectively.

The concentration of the reactants $c_a,c_b\text{ and }{c}_c$ at $t=2\text{ s}$ are $50,0,5.4135$ respectively.

The concentration of the reactants $c_a,c_b\text{ and }{c}_c$ at $t=3\text{ s}$ are $50,0,5.4135$ respectively.

Explanation of Solution

Given information:

The system of equations,

$\begin{array}{c}\frac{d{c}_a}{dt}=-10c_a{c}_c+c_b\\ \frac{d{c}_b}{dt}=10c_a{c}_c-c_b\\ \frac{d{c}_c}{dt}=-10c_a{c}_c+c_b-2c_c\end{array}$

Initial conditions, $c_a=50,c_b=0\text{ and }{c}_c=40$

Formula used:

To calculate the values of $c_a,c_b\text{ and }{c}_c$: Jacobi matrix is,

$J\left(c_a,c_b,c_c\right)=\left[\begin{array}{ccc}{f}_{c_a}\left(c_a,c_b,c_c\right)& f_{c_b}\left(c_a,c_b,c_c\right)& f_{c_c}\left(c_a,c_b,c_c\right)\\ g_{c_a}\left(c_a,c_b,c_c\right)& g_{c_b}\left(c_a,c_b,c_c\right)& g_{c_c}\left(c_a,c_b,c_c\right)\\ h_{c_a}\left(c_a,c_b,c_c\right)& h_{c_b}\left(c_a,c_b,c_c\right)& h_{c_c}\left(c_a,c_b,c_c\right)\end{array}\right]$

Eigen value $\lambda$ of the matrix A can be calculated as,

$\left|A-\lambda I\right|=0$

Calculation:

Consider the system of first order nonlinear differential equation of reactants

$\begin{array}{c}\frac{d{c}_a}{dt}=-10c_a{c}_c+c_b\\ \frac{d{c}_b}{dt}=10c_a{c}_c-c_b\\ \frac{d{c}_c}{dt}=-10c_a{c}_c+c_b-2c_c\end{array}$

To calculate equilibrium points, consider the equations given below:

$\begin{array}{c}\frac{d{c}_a}{dt}=0\\ \frac{d{c}_b}{dt}=0\\ \frac{d{c}_c}{dt}=0\end{array}$

Compare the system of first order nonlinear differential equations with the above equations,

$\begin{array}{c}-10c_a{c}_c+c_b=0\\ 10c_a{c}_c-c_b=0\\ -10c_a{c}_c+c_b-2c_c=0\end{array}$

Therefore, the equilibrium point is,

$c_a=0,c_b=0,c_c=0$

Suppose, the system of non-linear differential equations are equal to some functions, that is,

$\begin{array}{c}\frac{d{c}_a}{dt}=f\left(c_a,c_b,c_c\right)\\ \frac{d{c}_b}{dt}=g\left(c_a,c_b,c_c\right)\\ \frac{d{c}_c}{dt}=h\left(c_a,c_b,c_c\right)\end{array}$

Now, compare these equations with system of non-linear differential equations,

$\begin{array}{c}f\left(c_a,c_b,c_c\right)=-10c_a{c}_c+c_b\\ g\left(c_a,c_b,c_c\right)=10c_a{c}_c-c_b\\ h\left(c_a,c_b,c_c\right)=-10c_a{c}_c+c_b-2c_c\end{array}$

Now, find the Jacobian matrix,

$J\left(c_a,c_b,c_c\right)=\left[\begin{array}{ccc}{f}_{c_a}\left(c_a,c_b,c_c\right)& f_{c_b}\left(c_a,c_b,c_c\right)& f_{c_c}\left(c_a,c_b,c_c\right)\\ g_{c_a}\left(c_a,c_b,c_c\right)& g_{c_b}\left(c_a,c_b,c_c\right)& g_{c_c}\left(c_a,c_b,c_c\right)\\ h_{c_a}\left(c_a,c_b,c_c\right)& h_{c_b}\left(c_a,c_b,c_c\right)& h_{c_c}\left(c_a,c_b,c_c\right)\end{array}\right]$

Then, the Jacobian matrix at the equilibrium points $c_a=0,c_b=0,c_c=0$ is,

$\begin{array}{c}J\left(0,0,0\right)=\left[\begin{array}{ccc}{f}_{c_a}\left(0,0,0\right)& f_{c_b}\left(0,0,0\right)& f_{c_c}\left(0,0,0\right)\\ g_{c_a}\left(0,0,0\right)& g_{c_b}\left(0,0,0\right)& g_{c_c}\left(0,0,0\right)\\ h_{c_a}\left(0,0,0\right)& h_{c_b}\left(0,0,0\right)& h_{c_c}\left(0,0,0\right)\end{array}\right]\\ =\left[\begin{array}{ccc}0& 1& 0\\ 0& -1& 0\\ 0& 1& -2\end{array}\right]\end{array}$

Now, the linearized system corresponding to nonlinear system of differential equation is,

$\begin{array}{c}{\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)}^{\prime }=J\left(0,0,0\right)\left(\begin{array}{c}{c}_a-0\\ c_b-0\\ c_c-0\end{array}\right)\\ =\left[\begin{array}{ccc}0& 1& 0\\ 0& -1& 0\\ 0& 1& -2\end{array}\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)\end{array}$

Let, $A$ be the coefficient matrix of the above system,

$A=\left[\begin{array}{ccc}0& 1& 0\\ 0& -1& 0\\ 0& 1& -2\end{array}\right]$

Suppose, $\lambda$ be the eigenvalue of the matrix $A$.

Thus,

$\begin{array}{c}\left|A-\lambda I\right|=0\\ \left|\begin{array}{ccc}0-\lambda & 1& 0\\ 0& -1-\lambda & 0\\ 0& 1& -2-\lambda \end{array}\right|=0\end{array}$

Now calculate the determinant as,

$\begin{array}{c}\left(0-\lambda \right)\left[\left(-1-\lambda \right)\left(-2-\lambda \right)-0\right]-1\left(0\left(-2-\lambda \right)-0\right)=0\\ \lambda \left[\left(1+\lambda \right)\left(2+\lambda \right)\right]=0\\ \lambda =-2,-1,0\end{array}$

Therefore, the eigenvalues of the matrix are $\lambda =-2,-1,0$

Now, find the eigenvector corresponding to each eigenvalue of the matrix.

The eigenvector is,

$\left[A-\lambda I\right]X=0$

Where, $X=\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)$

Substitute the value of X in $\left[A-\lambda I\right]X=0$,

$\left[A-\lambda I\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=0$

Put $\lambda =-2$ in $\left[A-\lambda I\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=0$,

$\begin{array}{c}\left[A+2I\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=0\\ \left[\left[\begin{array}{ccc}0& 1& 0\\ 0& -1& 0\\ 0& 1& -2\end{array}\right]+2\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)\\ \left[\begin{array}{ccc}2& 1& 0\\ 0& 1& 0\\ 0& 1& 0\end{array}\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)\\ \left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)\end{array}$

Put $\lambda =-1$ in $\left[A-\lambda I\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=0$,

$\begin{array}{c}\left[A+I\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=0\\ \left[\left[\begin{array}{ccc}0& 1& 0\\ 0& -1& 0\\ 0& 1& -2\end{array}\right]+\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)\\ \left[\begin{array}{ccc}1& 1& 0\\ 0& 0& 0\\ 0& 1& -1\end{array}\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)\\ \left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=\left(\begin{array}{c}1\\ -1\\ -1\end{array}\right)\end{array}$

Put $\lambda =0$ in $\left[A-\lambda I\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=0$,

$\begin{array}{c}\left[A+I\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=0\\ \left[\left[\begin{array}{ccc}0& 1& 0\\ 0& -1& 0\\ 0& 1& -2\end{array}\right]+0\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)\\ \left[\begin{array}{ccc}0& 1& 0\\ 0& -1& 0\\ 0& 1& -2\end{array}\right]\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)\\ \left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)\end{array}$

Therefore, the eigenvector corresponding to each eigenvalue of the matrix are respectively

$X=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right),\left(\begin{array}{c}1\\ -1\\ -1\end{array}\right),\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)$

Hence, the solution of the system of nonlinear differential equation is,

$\begin{array}{c}X=C_1{X}_1{e}^{{\lambda }_{1}t}+C_2{X}_2{e}^{{\lambda }_{2}t}+C_3{X}_3{e}^{{\lambda }_{3}t}\\ =C_1\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)e^{-2t}+C_2\left(\begin{array}{c}1\\ -1\\ -1\end{array}\right)e^{-t}+C_3\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)e^{0\times t}\\ =C_1\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)e^{-2t}+C_2\left(\begin{array}{c}1\\ -1\\ -1\end{array}\right)e^{-t}+C_3\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)\end{array}$

After solve the above equation,

$\begin{array}{c}\left(\begin{array}{c}{c}_a\\ c_b\\ c_c\end{array}\right)=C_1\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)e^{-2t}+C_2\left(\begin{array}{c}1\\ -1\\ -1\end{array}\right)e^{-t}+C_3\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)\\ =\left(\begin{array}{c}0\\ 0\\ C_1{e}^{-2t}\end{array}\right)+\left(\begin{array}{c}{C}_2{e}^{-t}\\ -C_2{e}^{-t}\\ -C_2{e}^{-t}\end{array}\right)+\left(\begin{array}{c}{C}_3\\ 0\\ 0\end{array}\right)\\ =\left(\begin{array}{c}{C}_2{e}^{-t}+C_3\\ -C_2{e}^{-t}\\ C_1{e}^{-2t}-C_2{e}^{-t}\end{array}\right)\end{array}$

Then the values of $c_a,c_b\text{ and }{c}_c$ are,

$\begin{array}{c}{c}_a\left(t\right)=C_2{e}^{-t}+C_3\\ c_b\left(t\right)=-C_2{e}^{-t}\\ c_c\left(t\right)=C_1{e}^{-2t}-C_2{e}^{-t}\end{array}$

The initial conditionsgiven as,

$c_a\left(0\right)=50,c_b\left(0\right)=0,c_c\left(0\right)=40$

Now, apply the initial condition in the above equations,

$\begin{array}{c}{c}_a\left(0\right)=C_2{e}^{-0}+C_3\\ c_b\left(0\right)=-C_2{e}^{-0}\\ c_c\left(0\right)=C_1{e}^{-2\times 0}-C_2{e}^{-0}\end{array}$

This imply that,

$\begin{array}{c}50=C_2+C_3\\ 0=-C_2\\ 40=C_1-C_2\end{array}$

Then, $C_1=40,C_2=0,C_3=50$

Substitute, the value of $C_1,C_2\text{ and }{C}_3$ in $c_a,c_b\text{ and }{c}_c$

$\begin{array}{c}{c}_a\left(t\right)=50\\ c_b\left(t\right)=0\\ c_c\left(t\right)=40e^{-2t}\end{array}$

The concentration at $t=0\text{ s}$ are,

$\begin{array}{c}{c}_a\left(t\right)=50\\ c_b\left(t\right)=0\\ c_c\left(t\right)=40\end{array}$

Therefore, theconcentration of the reactants $c_a,c_b\text{ and }{c}_c$ at $t=0\text{ s}$ are $50,0,40$ respectively.

Now, the concentration at $t=1\text{ s}$ are,

$\begin{array}{c}{c}_a\left(t\right)=50\\ c_b\left(t\right)=0\\ c_c\left(t\right)=40e^{-2}\\ =5.4135\end{array}$

Therefore, the concentration of the reactants $c_a,c_b\text{ and }{c}_c$ at $t=1\text{ s}$ are $50,0,5.4135$ respectively.

Now, the concentration at $t=2\text{ s}$ are,

$\begin{array}{c}{c}_a\left(t\right)=50\\ c_b\left(t\right)=0\\ c_c\left(t\right)=40e^{-2\times 2}\\ =0.7327\end{array}$

Therefore, the concentration of the reactants $c_a,c_b\text{ and }{c}_c$ at $t=2\text{ s}$ are $50,0,5.4135$ respectively.

Now, the concentration at $t=3\text{ s}$ are,

$\begin{array}{c}{c}_a\left(t\right)=50\\ c_b\left(t\right)=0\\ c_c\left(t\right)=40e^{-2\times 3}\\ =0.09916\end{array}$

Use the following MATLAB code to plot the concentrationvalues,

clear;clc;

% enter the value or expression of the concentrations

c_a = 50;

c_b = 0;

% define the range of t

t = linspace(0,3,20);

c_c = 40.*exp(-2.*t);

% plot the results

plot([0,3],[c_a, c_a],'r',[0,3],[c_b, c_b],'g', t, c_c,'k')

legend('c_a','c_b','c_c')

xlabel('t')

Execute the above to obtain the plot as,

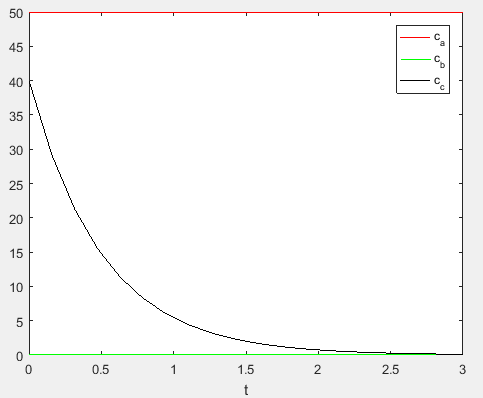
Therefore, the concentration of the reactants $c_a,c_b\text{ and }{c}_c$ at $t=3\text{ s}$ are $50,0,5.4135$ respectively.

Hence, the concentration of the reactants $c_a\text{ and }{c}_b$ is constant through the time $t$ but concentration of the reactant $c_c$ is decreasing rapidly with increase in time $t$.