
Concept explainers
The temperature distribution in a tapered conical cooling fin (Fig. P28.48) is described by the following differential equation, which has been nondimensionalized
where
where
Solve this equation for the temperature distribution using finite difference methods. Use second-order accurate finite difference analogues for the derivatives. Write a computer program to obtain the solution and plot temperature versus axial distance for various values of
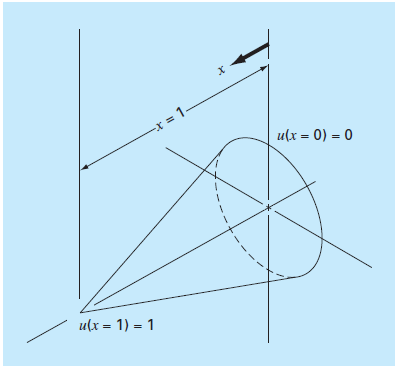
FIGURE P28.48
Want to see the full answer?
Check out a sample textbook solution
Chapter 28 Solutions
Numerical Methods for Engineers
- 2 Q/Given H (x,y) = x² + y² - y² Find the Hamiltonian System and prove it is first integral-arrow_forwardQ2) A: Find the region where ODEs has no limit cycle: x = y + x³ y=x+y+y³ 6arrow_forwardQ3)A: Given H(x,y)=x2-x+ y²as a first integral of an ODEs, find this ODES corresponding to H(x,y) and show the phase portrait by using Hartman theorem and by drawing graph of H(x,y)-e. Discuss the stability of critical points of the corresponding ODEs.arrow_forward
- Using Karnaugh maps and Gray coding, reduce the following circuit represented as a table and write the final circuit in simplest form (first in terms of number of gates then in terms of fan-in of those gates). HINT: Pay closeattention to both the 1’s and the 0’s of the function.arrow_forwardRecall the RSA encryption/decryption system. The following questions are based on RSA. Suppose n (=15) is the product of the two prime numbers 3 and 5.1. Find an encryption key e for for the pair (e, n)2. Find a decryption key d for for the pair (d, n)3. Given the plaintext message x = 3, find the ciphertext y = x^(e) (where x^e is the message x encoded with encryption key e)4. Given the ciphertext message y (which you found in previous part), Show that the original message x = 3 can be recovered using (d, n)arrow_forwardTheorem 1: A number n ∈ N is divisible by 3 if and only if when n is writtenin base 10 the sum of its digits is divisible by 3. As an example, 132 is divisible by 3 and 1 + 3 + 2 is divisible by 3.1. Prove Theorem 1 2. Using Theorem 1 construct an NFA over the alphabet Σ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}which recognizes the language {w ∈ Σ^(∗)| w = 3k, k ∈ N}.arrow_forward
- Recall the RSA encryption/decryption system. The following questions are based on RSA. Suppose n (=15) is the product of the two prime numbers 3 and 5.1. Find an encryption key e for for the pair (e, n)2. Find a decryption key d for for the pair (d, n)3. Given the plaintext message x = 3, find the ciphertext y = x^(e) (where x^e is the message x encoded with encryption key e)4. Given the ciphertext message y (which you found in previous part), Show that the original message x = 3 can be recovered using (d, n)arrow_forwardFind the sum of products expansion of the function F(x, y, z) = ¯x · y + x · z in two ways: (i) using a table; and (ii) using Boolean identities.arrow_forwardGive both a machine-level description (i.e., step-by-step description in words) and a state-diagram for a Turing machine that accepts all words over the alphabet {a, b} where the number of a’s is greater than or equal to the number of b’s.arrow_forward
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,






