
Concept explainers
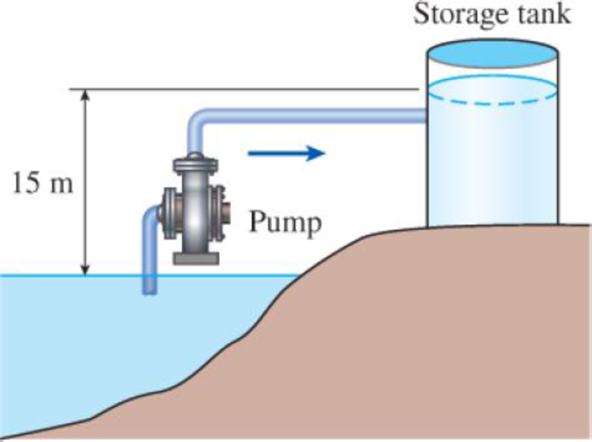
Water is pumped from a lake to a storage tank 15 m above at a rate of 70 L/s while consuming 15.4 kW of electric power. Disregarding any frictional losses in the pipes and any changes in kinetic energy, determine (a) the overall efficiency of the pump–motor unit and (b) the pressure difference between the inlet and the exit of the pump.
FIGURE P2–69
(a)
The overall efficiency of the pump-motor unit.
Answer to Problem 69P
The overall efficiency of the pump-motor is
Explanation of Solution
Write the mass flow rate of water.
Here, the volumetric flow rate of water is
The potential energy at point 1 is considered as 0
Write the equation of potential energy at point 2.
Here, acceleration due to gravity is g and lake surface at point 2 is
Calculate the rate at which mechanical energy of fluid supplied to the pump.
Here, the mechanical energy of water inlet and outlet are
Calculate the overall efficiency of the combined pump-motor.
Here, and electric power consumption is
Conclusion:
Substitute
Substitute
Substitute 70 kg/s for
Substitute 10.3 kW for
Thus, the overall efficiency of the pump-motor is
(b)
The pressure difference between the inlet and the exit of the pump.
Answer to Problem 69P
The pressure difference between the inlet and the exit of the pump is
Explanation of Solution
Calculate the rate at which mechanical energy of fluid supplied by the pump.
Here, change in the pressure of water is
Conclusion:
Substitute 10.3 kJ/s for
Thus, the pressure difference between the inlet and the exit of the pump is
Want to see more full solutions like this?
Chapter 2 Solutions
THERMODYNAMICS (LL)-W/ACCESS >CUSTOM<
Additional Engineering Textbook Solutions
Starting Out with Programming Logic and Design (5th Edition) (What's New in Computer Science)
Automotive Technology: Principles, Diagnosis, And Service (6th Edition) (halderman Automotive Series)
Mechanics of Materials (10th Edition)
Vector Mechanics for Engineers: Statics and Dynamics
Thinking Like an Engineer: An Active Learning Approach (4th Edition)
Fluid Mechanics: Fundamentals and Applications
- a ship 150 m long and 20.5 m beam floats at a draught of8 m and displaces 19 500 tonne. The TPC is 26.5 and midshipsection area coefficient 0.94. Calculate the block, prismatic andwaterplane area coefficients.arrow_forwardA vessel loads 680 t fuel between forward and aft deep tanks. centre of gravity of forward tank is 24m forward of ships COG. centre to centre between tanks is 42 m. how much in each tank to keep trim the samearrow_forwardBeam of a vessel is 11% its length. Cw =0.72. When floating in SW of relative denisity 1.03, TPC is 0.35t greater than in freshwater. Find the length of the shiparrow_forward
- An inclining experiment was carried out on a ship of 4000tonne displacement, when masses of 6 tonne were moved transverselythrough 13.5 m. The deflections of a 7.5 m pendulurnwere 81, 78, 85, 83, 79, 82, 84 and 80 mm respectively.Caiculate the metacentric height.arrow_forwardA ship of 10 000 tonne displacement has a waterplanearea of 1300 m2. The ship loads in water of 1.010 t/m3 andmoves into water of 1.026 t/m3. Find the change in meandraughtarrow_forwardA ship of 7000 tonne displacement has a waterplane areaof 1500 m2. In passing from sea water into river water of1005 kg/m3 there is an increase in draught of 10 cm. Find the Idensity of the sea water.arrow_forward
- A ship has 300 tonne of cargo in the hold, 24 m forward ofmidships. The displacement of the vessel is 6000 tonne and its centre of gravity is 1.2 m forward of midships.Find the new position of the centre of gravity if this cargo ismoved to an after hold, 40 m from midshipsarrow_forwardSketch and describe how ships are supported in dry dock. When and where does the greatest amount of stresses occur?arrow_forwardSketch and desribe a balanced rudder and how it is suspendedarrow_forward
- A ship 140 m long and 18 m beam floats at a draught of9 m. The immersed cross-sectionai areas at equai intervais are 5,60, 116, 145, 152, 153, 153, 151, 142, 85 and 0 m2 respectively.Calculate:(a) displacement(b) block coefficient(c) midship section area coefficient(d) prismatic coefficient.arrow_forwardA steamer has waterplane area 1680m2 recorded in water with relative denisty 1.013. Displacement = 1200 t, calculate difference in draught in salwater reltive denisity 1.025.arrow_forwardrelative velocity 11.72 m/s is correct, need help finding the angle pleasearrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





