
Perform the first computation in Sec. 28.1, but for the casewhere
To calculate: The solution for c if thedifferential equation for mass balance of single reactor is
Answer to Problem 1P
Solution:
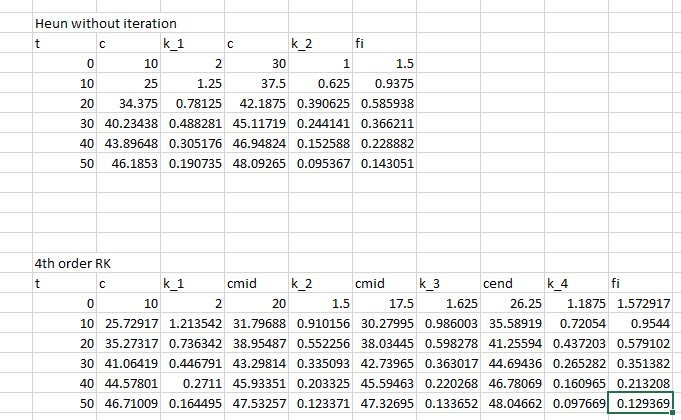
The solution for c by the Heun method where
| Heun withoutiteration | |
| t | c |
| 0 | 10 |
| 10 | 25 |
| 20 | 34.375 |
| 30 | 40.23438 |
| 40 | 43.89648 |
| 50 | 46.1853 |
The solution for c by fourth-order RK method where
| 4th order RK | |
| t | c |
| 0 | 10 |
| 10 | 25.72917 |
| 20 | 35.27317 |
| 30 | 41.06419 |
| 40 | 44.57801 |
| 50 | 46.71009 |
Explanation of Solution
Given Information:
The differential equation for mass balance of single reactor is,
The values,
The analytical equation for mass balance of single reactor is,
Formula used:
The iteration formula for Heun’s method is,
The fourth-order RK method for
Where,
Calculation:
Consider the analytical equation for mass balance of single reactor is,
Substitute the values
Now, use VB code to determine c at different value of t using Heun’s method and RK4 method as below,
The following output gets displayed in the excel after the execution of the above code:
To draw the graph, use excel as below,
Step 1: Select cells from B5 to B10 and C5 to C10, then go to Insert tab and select the Line option from Charts subgroup.
Step 2: Select cells from B17 to B22 and C17 to C22, then go to Insert tab and select the Line option from Charts subgroup
Step 3: Merge the graphs.
The graph obtained is,
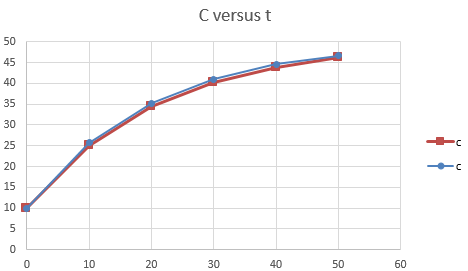
Hence, both the method gives the same results.
Want to see more full solutions like this?
Chapter 28 Solutions
Numerical Methods for Engineers
- Let Χ be a real-valued character (mod k). Let k S = Σnx(n). n=1 If (a, k) = 1, ax(a)S = S (mod k). (iii) Write k = 2ºq where q is odd. Show that there is an integer a with (a, k) = 1 such that a = 3 (mod 2ª) and a = 2 (mod q). Deduce that 12S = 0 (mod k).arrow_forwardProve that (1) Σσς (α) μ(η/α) = n d/n (ii) Σσς(d) = η Σσο(α)/d d❘n d❘n (iii) σ (d) σ (n/d) = Σ d³oo(d) σo(n/d). d|n dnarrow_forwardhow to do part b,carrow_forward
- If p = 5 (mod 8), where p is prime, show that p|2 (P-1)/2 + 1. State and prove the corresponding result when p = 7 (mod 8). Deduce that 250 + 1 and 251 1 are composite. -arrow_forwardWhy the character no change for my remark?arrow_forwardIn preparing for the upcoming holiday season, Fresh Toy Company (FTC) designed a new doll called The Dougie that teaches children how to dance. The fixed cost to produce the doll is $100,000. The variable cost, which includes material, labor, and shipping costs, is $31 per doll. During the holiday selling season, FTC will sell the dolls for $39 each. If FTC overproduces the dolls, the excess dolls will be sold in January through a distributor who has agreed to pay FTC $10 per doll. Demand for new toys during the holiday selling season is extremely uncertain. Forecasts are for expected sales of 60,000 dolls with a standard deviation of 15,000. The normal probability distribution is assumed to be a good description of the demand. FTC has tentatively decided to produce 60,000 units (the same as average demand), but it wants to conduct an analysis regarding this production quantity before finalizing the decision. (a) Determine the equation for computing FTC's profit for given values of the…arrow_forward
- To generate leads for new business, Gustin Investment Services offers free financial planning seminars at major hotels in Southwest Florida. Gustin conducts seminars for groups of 25 individuals. Each seminar costs Gustin $3,700, and the average first-year commission for each new account opened is $5,200. Gustin estimates that for each individual attending the seminar, there is a 0.01 probability that individual will open a new account. (a) Determine the equation for computing Gustin's profit per seminar, given values of the relevant parameters. Profit = (3,700 x 5,200) - New Accounts Opened Profit = 5,200 - (New Accounts Opened x 3,700) Profit = (New Accounts Opened x 3,700) - 5,200 Profit = New Accounts Opened - (5,200 × 3,700) Profit = (New Accounts Opened x 5,200) - 3,700 (b) What type of random variable is the number of new accounts opened? Hint: Review Appendix 12.1 for descriptions of various types of probability distributions. continuous integer uniform normal discrete uniform…arrow_forwardStrassel Investors buys real estate, develops it, and resells it for a profit. A new property is available, and Bud Strassel, the president and owner of Strassel Investors, believes if he purchases and develops this property, it can then be sold for $158,000. The current property owner has asked for bids and stated that the property will be sold for the highest bid in excess of $100,000. Two competitors will be submitting bids for the property. Strassel does not know what the competitors will bid, but he assumes for planning purposes that the amount bid by each competitor will be uniformly distributed between $100,000 and $148,000. (a) What is the estimate of the probability Strassel will be able to obtain the property using a bid of $128,000? (Use at least 5,000 trials. Round your answer three decimal places.) (b) How much does Strassel need to bid to be assured of obtaining the property? $128,000 $138,000 $148,000 (c) Use the simulation model to compute the profit for each trial of…arrow_forwardGrear Tire Company has produced a new tire with an estimated mean lifetime mileage of 34,500 miles. Management also believes that the standard deviation is 4,500 miles and that tire mileage is normally distributed. To promote the new tire, Grear has offered to refund a portion of the purchase price if the tire fails to reach 30,000 miles before the tire needs to be replaced. Specifically, for tires with a lifetime below 30,000 miles, Grear will refund a customer $1 per 100 miles short of 30,000. Construct a simulation model to answer the following questions. (Use at least 1,000 trials.) (a) For each tire sold, what is the average cost of the promotion (in $)? (Round your answer to two decimal places.) (b) What is the probability that Grear will refund more than $25 for a tire? (Round your answer to three decimal places.)arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,

