Chapter 2.1, Problem 85E

Price-demand. A company manufactures memory chips for microcomputers. Its marketing research department, using statistical techniques, collected the data shown in Table $8$, where $p$ is the wholesale price per chip at which $x$ million chips can be sold. Using special analytical techniques (regression analysis), an analyst produced the following price demand function to model the data:

$p\left(x\right)=75-3x1\le x\le 20$

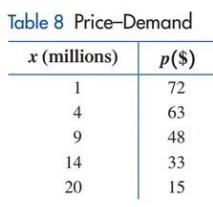
(a) Plot the data points in Table $8$, and sketch a graph of the price-demand function in the same coordinate system.

(b) What would be the estimated price per chip for a demand of $7$ million chips? For a demand of $11$ million chips?