Chapter 2.1, Problem 35E

Native languages: The following frequency distribution presents the number of households (in thousands) categorized by the language spoken at home, for the cities of New York and Los Angeles in the year 2009. The Total column presents the numbers of households in both cities combined.

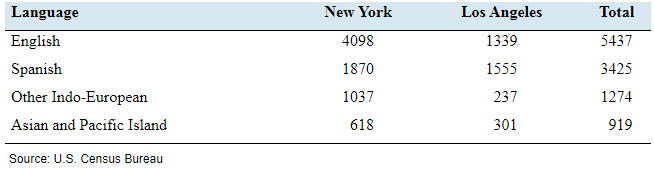
Source: US. Census Bureau

1. Construct a frequency bar graph for each city.
2. Construct a frequency bar graph for the total.
3. Construct a relative frequency bar graph for each city.
4. Construct a relative frequency bar graph for the total.
5. Explain why the heights of the bars for the frequency bar graph for the total are equal to the sums of the heights for the individual cities.
6. Explain why the heights of the bars for the relative frequency bar graph for the total are not equal to the sums of the heights for the individual cities.

To determine

To construct:A frequency bar graph for each city.

Explanation of Solution

Given information:The following frequency distribution presents the number of households (in thousands) categorized by the language spoken at home, for the cities of NewYork and Los An

geles in the year 2009. The total column presents the number of households in both cities combined

Language	New York	Los Angeles	Total
English	4098	1339	5437
Spanish	1870	1555	3425
Other Indo-European	1037	237	1274
Asian and Pacific Island	618	301	919

.

Solution:

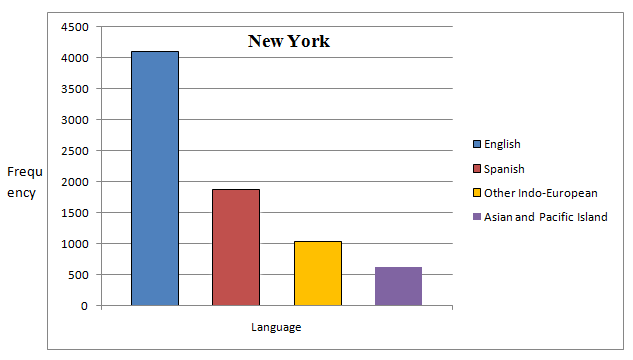
From the given table, the frequency bar graph for New York is given by

  

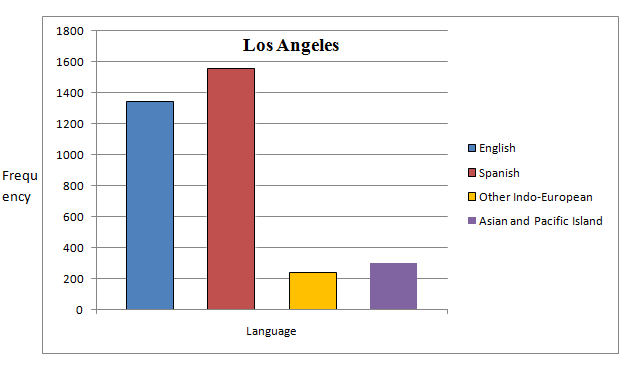
The frequency bar graph for Los Angeles is given by

  

To determine

To construct: A frequency bar graph for the total.

Explanation of Solution

Given information: The following frequency distribution presents the number of households (in thousands) categorized by the language spoken at home, for the cities of New York and Los An

geles in the year 2009. The total column presents the number of households in both cities combined

Language	New York	Los Angeles	Total
English	4098	1339	5437
Spanish	1870	1555	3425
Other Indo-European	1037	237	1274
Asian and Pacific Island	618	301	919

.

Solution:

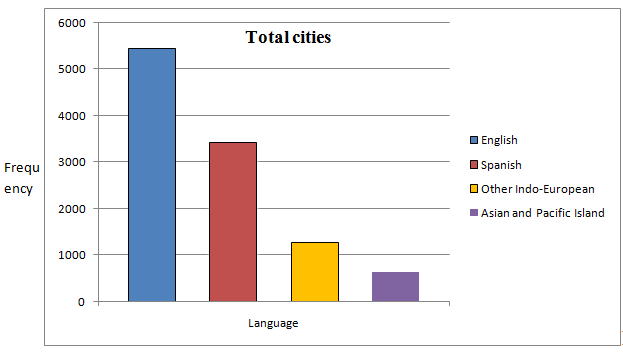
From the given table, the frequency bar graph for the total is given by

  

To determine

To construct:A relative frequency bar graph for each city.

Explanation of Solution

The following frequency distribution presents the number of households (in thousands) categorized by the language spoken at home, for the cities of New York and Los An

geles in the year 2009. The total column presents the number of households in both cities combined

Language	New York	Los Angeles	Total
English	4098	1339	5437
Spanish	1870	1555	3425
Other Indo-European	1037	237	1274
Asian and Pacific Island	618	301	919

Formula used: $Relativefrequency=\frac{Frequency}{}$

  $Relativefrequency=\frac{Frequency}{ Sum\text{ of all }Frequency}$

Solution:

From the given table,

The sum of all frequency for New York city is 7623.

The table of relative frequency for New York city is given by

Language	New York	Relative Frequency
English	4098	$\frac{4098}{7623}=0.538$
Spanish	1870	$\frac{1870}{7623}=0.245$
Other Indo-European	1037	$\frac{1037}{7623}=0.136$
Asian and Pacific Island	618	$\frac{618}{7623}=0.081$

From the given table, the relative frequency bar graph for New York is given by

  

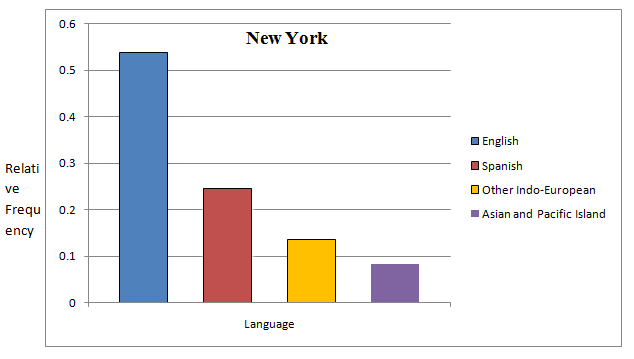
The sum of all frequency for Los Angeles is 3432.

The table of relative frequency for Los Angeles city is given by

Language	Los Angeles	Relative Frequency
English	1339	$\frac{1339}{3432}=0.390$
Spanish	1555	$\frac{1555}{3432}=0.453$
Other Indo-European	237	$\frac{237}{3432}=0.069$
Asian and Pacific Island	301	$\frac{301}{3432}=0.088$

The relative frequency bar graph for Los Angeles is given by

  

To determine

To construct: A relative frequency bar graph for the total.

Explanation of Solution

Given information: The following frequency distribution presents the number of households (in thousands) categorized by the language spoken at home, for the cities of New York and Los An

geles in the year 2009. The total column presents the number of households in both cities combined

Language	New York	Los Angeles	Total
English	4098	1339	5437
Spanish	1870	1555	3425
Other Indo-European	1037	237	1274
Asian and Pacific Island	618	301	919

Formula used: $Relativefrequency=\frac{Frequency}{}$

  $Relativefrequency=\frac{Frequency}{ Sum\text{ of all }Frequency}$

Solution:

From the given table,

The sum of all frequency for total city is 11055.

The table of relative frequency for New York city is given by

Language	Total	Relative Frequency
English	5437	$\frac{5437}{11055}=0.492$
Spanish	3425	$\frac{3425}{11055}=0.310$
Other Indo-European	1274	$\frac{1274}{11055}=0.115$
Asian and Pacific Island	919	$\frac{919}{11055}=0.083$

From the given table, the relative frequency bar graph for the total is given by

  

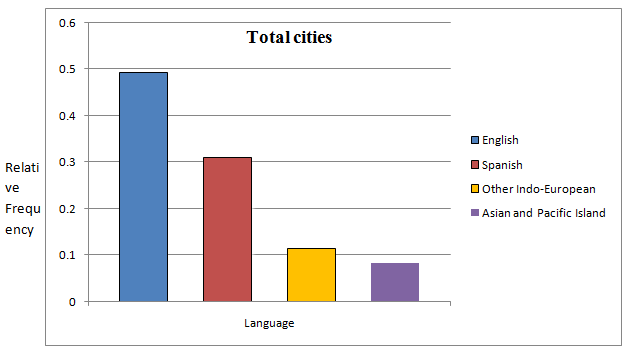
To determine

To explain: The heights of the bars for the frequency bar graph for the total are equal to the sum of the heights for the individual cities.

Explanation of Solution

Given information: The following frequency distribution presents the number of households (in thousands) categorized by the language spoken at home, for the cities of New York and Los An

geles in the year 2009. The total column presents the number of households in both cities combined

Language	New York	Los Angeles	Total
English	4098	1339	5437
Spanish	1870	1555	3425
Other Indo-European	1037	237	1274
Asian and Pacific Island	618	301	919

Since each total frequency of households is the sum of the frequencies for the cities of New York and Los Angeles, therefore, the heights of the bars for the frequency bar graph for the total are equal to the sum of the heights for the individual cities.

To determine

To explain: The heights of the bars for the relative frequency bar graph for the total are not equal to the sum of the heights for the individual cities.

Explanation of Solution

Given information: The following frequency distribution presents the number of households (in thousands) categorized by the language spoken at home, for the cities of New York and Los An

geles in the year 2009. The total column presents the number of households in both cities combined

Language	New York	Los Angeles	Total
English	4098	1339	5437
Spanish	1870	1555	3425
Other Indo-European	1037	237	1274
Asian and Pacific Island	618	301	919

The relative frequency is the frequency divided by the sum of all frequency.

The sum of all frequencies for each city is not equal to the sum of all total frequencies; therefore, the sum of relative frequency for each city will not be equal to the relative frequency for total.

Hence, the heights of the bars for the relative frequency bar graph for the total are not equal to the sum of the heights for the individual cities.