Fox And Mcdonald's Introduction To Fluid Mechanics
9th Edition
ISBN: 9781118921876
Author: Pritchard, Philip J.; Leylegian, John C.; Bhaskaran, Rajesh
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2, Problem 74P
The viscous boundary layer velocity profile shown in Fig. 2.15 can be approximated by a cubic equation,
The boundary condition is u = U (the free stream velocity) at the boundary edge δ (where the viscous friction becomes zero). Find the values of a, b, and c.
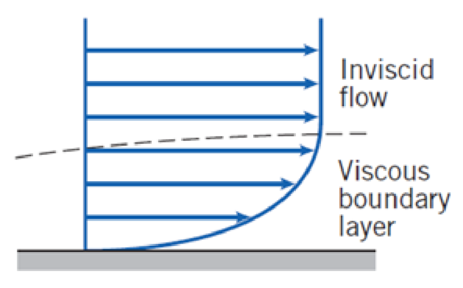
Fig. 2.15 Schematic of a boundary layer.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
See question attached in photo.
help
Two branches of water pipe merge to form a larger diameter as shown figure below. At a location at the junction (before completely merging) the nonuniform profile is observed at the depth of 6 ftDetermine the value of V (ft / s) .
Chapter 2 Solutions
Fox And Mcdonald's Introduction To Fluid Mechanics
Ch. 2 - For the velocity fields given below, determine:...Ch. 2 - For the velocity fields given below, determine:...Ch. 2 - A viscous liquid is sheared between two parallel...Ch. 2 - For the velocity field V=Ax2yi+Bxy2j, where A = 2...Ch. 2 - A fluid flow has the following velocity...Ch. 2 - When an incompressible, nonviscous fluid flows...Ch. 2 - For the free vortex flow the velocities are t =...Ch. 2 - For the forced vortex flow the velocities are t =...Ch. 2 - A velocity field is specified as V=axyi+by2j,...Ch. 2 - A velocity field is given by V=ax3i+bxy3j, where a...
Ch. 2 - The velocity for a steady, incompressible flow in...Ch. 2 - The flow field for an atmospheric flow is given by...Ch. 2 - For the velocity field V=AxiAyj,, where A = 2s 1....Ch. 2 - A velocity field in polar coordinates is given...Ch. 2 - The flow of air near the Earths surface is...Ch. 2 - A velocity field is given by V=aytibxj, where a =...Ch. 2 - Air flows downward toward an infinitely wide...Ch. 2 - Consider the flow described by the velocity field...Ch. 2 - Consider the velocity field V = axi + by(1 + ct)...Ch. 2 - Consider the flow field given in Eulerian...Ch. 2 - A velocity field is given by V=axti+byj, where A =...Ch. 2 - Consider the garden hose of Fig. 2.5. Suppose the...Ch. 2 - Consider the velocity field of Problem 2.18. Plot...Ch. 2 - Streaklines are traced out by neutrally buoyant...Ch. 2 - Consider the flow field V=axti+bj, where a = 1/s2...Ch. 2 - A flow is described by velocity field V=ay2i+bj,...Ch. 2 - Tiny hydrogen bubbles are being used as tracers to...Ch. 2 - A flow is described by velocity field V=ai+bxj,...Ch. 2 - A flow is described by velocity field V=ayi+btj,...Ch. 2 - A flow is described by velocity field V=ati+bj,...Ch. 2 - The variation with temperature of the viscosity of...Ch. 2 - The variation with temperature of the viscosity of...Ch. 2 - Some experimental data for the viscosity of helium...Ch. 2 - The velocity distribution for laminar flow between...Ch. 2 - What is the ratio between the viscosities of air...Ch. 2 - Calculate velocity gradients and shear stress for...Ch. 2 - A very large thin plate is centered in a gap of...Ch. 2 - A female freestyle ice skater, weighing 100 lbf,...Ch. 2 - A block of mass 10 kg and measuring 250 mm on each...Ch. 2 - A 73-mm-diameter aluminum (SG = 2.64) piston of...Ch. 2 - A vertical gap 25 mm wide of infinite extent...Ch. 2 - A cylinder 8 in. in diameter and 3 ft long is...Ch. 2 - Crude oil at 20C fills the space between two...Ch. 2 - The piston in Problem 2.40 is traveling at...Ch. 2 - A block of mass M slides on a thin film of oil....Ch. 2 - A block 0.1 m square, with 5 kg mass, slides down...Ch. 2 - A torque of 4 N m is required to rotate the...Ch. 2 - A circular disk of diameter d is slowly rotated in...Ch. 2 - The fluid drive shown transmits a torque T for...Ch. 2 - A block that is a mm square slides across a flat...Ch. 2 - In a food-processing plant, honey is pumped...Ch. 2 - SAE 10W-30 oil at 100C is pumped through a tube L...Ch. 2 - The lubricant has a kinematic viscosity of 2:8105...Ch. 2 - Calculate the approximate viscosity of the oil....Ch. 2 - Calculate the approximate power lost in friction...Ch. 2 - Fluids of viscosities 1 = 0.1 Ns/m2 and 2 = 0.15...Ch. 2 - A concentric cylinder viscometer may be formed by...Ch. 2 - A concentric cylinder viscometer is driven by a...Ch. 2 - A shaft with outside diameter of 18 mm turns at 20...Ch. 2 - A shock-free coupling for a low-power mechanical...Ch. 2 - A proposal has been made to use a pair of parallel...Ch. 2 - The cone and plate viscometer shown is an...Ch. 2 - A viscometer is used to measure the viscosity of a...Ch. 2 - A concentric-cylinder viscometer is shown. Viscous...Ch. 2 - Design a concentric-cylinder viscometer to measure...Ch. 2 - A cross section of a rotating bearing is shown....Ch. 2 - Small gas bubbles form in soda when a bottle or...Ch. 2 - You intend to gently place several steel needles...Ch. 2 - According to Folsom [6], the capillary rise h...Ch. 2 - Calculate and plot the maximum capillary rise of...Ch. 2 - Calculate the maximum capillary rise of water...Ch. 2 - Calculate the maximum capillary depression of...Ch. 2 - Water usually is assumed to be incompressible when...Ch. 2 - The viscous boundary layer velocity profile shown...Ch. 2 - In a food industry process, carbon tetrachloride...Ch. 2 - What is the Reynolds number of water at 20C...Ch. 2 - A supersonic aircraft travels at 2700 km/hr at an...Ch. 2 - SAE 30 oil at 100C flows through a 12-mm-diameter...Ch. 2 - A seaplane is flying at 100 mph through air at...Ch. 2 - An airliner is cruising at an altitude of 5.5 km...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Q.3b Prove that the pressure 'p' is independent of the transverse coordinate 'y' in the boundary layer and hence show that the boundary layer equation for a flow over flat plate is given by, a² u ди ди u +v== 9 əx Əy Əy² where v is the kinematic viscosity of the fluid (may use 'order of magnitude' approach).arrow_forwardA VISCOUS FLUID FLOWS BETWEEN TWO PARALLEL AND INFINITELY LARGE PLATES KEPT AT A DISTANCE 2H FROM EACH OTHER. THE UPPER PLATE IS AT Y = H AND THE LOWE... A viscous fluid flows between two parallel and infinitely large plates kept at a distance 2h from each other. The upper plate is at y = h and the lower plate is at y = - h. The considered fluid flows mono directionally along the x-direction under a constant pressure gradient K = -dP/dx. The transverse profile of velocity is given by : U(y) = K (h² - y²) U (y) = (h-y) U(y) = (h² - y²) U(y) = (y²) U(y) = K (h-y) 2h EU(y)arrow_forwardA viscous fluid of viscosity 2.48 Pa-s and density 884 kg/m³ is dragged by a rigid flat surface that moves upward with speed V, as shown. The velocity profile in the fluid layer is of the form, pg v(x) = (x? – 2hx) + V Find the minimum speed V for which the entire fluid layer moves upward. What are the minimum and maximum values of the shear stress in the layer? Assume the flow to be incompressible and fully developed. 5 mmarrow_forward
- 1. a).Show that the UNSTEADY velocity field given below represents a 2-dimensional incompressible flow. Assume the fluid density is constant. V = (xyt³ – yt?)î + (x – y²t³/2)f b). For the same velocity field, using Navier-Stokes equation to find the pressure gradient in x direction, namely ӘР for constant density p and viscosity u. Assume there is no body force; c). Also for the same velocity field, find the acceleration in y direction, a,.arrow_forwardAn incompressible viscous flow is contained between two parallel plates separated from each other by distance b. The flow is caused by the movement of the upper plate which has a velocity U, while the bottom plate is fixed. If U = 9.5 m/s and b = 3.2 cm, and there is no pressure gradient in the flow direction. a) Start with Navier-Stokes equations and determine the velocity at the point x = 7 cm and y= 0.56 cm. b) Calculate the magnitude of the vorticity at the same point. c) Calculate the rate of angular deformation at the same point. Work to 4 significant digits. Enter all values using base units or their combinations, i.e. m, m/s, Pa, N. Do not use multiples as e.g. mm, kPa. You can use values with exponents, such as 0.12e3.arrow_forwardAn incompressible fluid flows between two flat plates, driven by a constant pressure gradient, dP/dx, and the constant motion of one of the plates, with speed, U. The spacing between the plates is b and the viscosity of the fluid is µu. Define a coordinate system where -b/2 < y< b/2 (y = 0 midway between the plates). a. What is the Navier-Stokes equation for x-direction momentum for parallel flow. b. What are the boundary conditions for this case? c. Solve for the x-direction velocity profile between the plates, u(y). d. Integrate to show that the relationship between the volume flow rate (per unit width of the plate), the speed of the plate and the pressure gradient is given by: dP b3 + U 12µ 2 barrow_forward
- Fluid Mechanics. Fluid kinematics. The figure below represents the upper view of pillars, with circular sections of 0.5 m, which support a bridge. The figure also shows the river speeds before and after reaching the pillars. The width of the bridge is 2d. *Consider that in the symmetry section of the bridge there is no flow and the slightest force is exerted in the cross section. d Uniform speed (v) = 2 m/s d' fo) = 15 + V = = 1,5 +: Whereas d = 2 m and d' 1 m, determine: a) What possible control volumes could be used to resolve the issue? b) The flow rate per unit of length entering the plane of the image. c) The slightest force exerted by the river water in this pillar of the figure. d) Are there any generated momentum? If so, justify it.arrow_forwardQuestion 1 (Momentum equation) a) The velocity component of fluid flow is given by u = xy² v = -4x²y w = 0 By using Navier-Stokes equation, determine the pressure gradient in the y-direction, dp at point (2, 2). Assuming incompressible, steady flow and the gravity is in y- dy direction only. The fluid is water with a density of 1000 kg/m³ and the dynamic viscosity is 0.0009 Ns/m² respectively.arrow_forwardA flow is non-uniform when the magnitude of the parameters varies from point to point along the flow path. TRUE FALSEarrow_forward
- An incompressible viscous flow is contained between two parallel plates separated from each other by distance b. as shown in Figure 1. The flow is caused by the movement of the upper plate which has a velocity U, while the bottom plate is fixed. If U =7 m/s and b= 1 cm, and there is no pressure gradient in the flow direction. A.) Start with Navier-Stokes equations and determine the velocity at the point x = 3 cm and y= 0.41 cm. The value of the velocity is.B.) Calculate the magnitude of the vorticity at the same point. The magnitude value of vorticity. C.) Calculate the rate of angular deformation at the same point. The angular deformation valuearrow_forwardA solid cone of angle 2Ɵ, base r 0 , and density ρ c is rotating with initialangular velocity ω 0 inside a conical seat,as shown below. The clearance h is filled with oilof viscosity μ. Neglecting air drag, derive an analytical expression for thecone’s angular velocity ω(t) if there is noapplied torque.arrow_forward1 Consider a rapidly rotating (ie, in near geostrophic balance) Boussineq fluid on the f plane. A) Show that the pressure divided by the density scales as Φ ≈ fUL B) Show that the horizontal divergence of the geostrophic wind vanishes. Thus, argue that the scaling W ≈ UH = L is an overestimate for the magnitude of the vertical velocityarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Introduction to Kinematics; Author: LearnChemE;https://www.youtube.com/watch?v=bV0XPz-mg2s;License: Standard youtube license