Introduction To Computing Systems
3rd Edition
ISBN: 9781260150537
Author: PATT, Yale N., Patel, Sanjay J.
Publisher: Mcgraw-hill,
expand_more
expand_more
format_list_bulleted
Question
Chapter 2, Problem 34E
a.
Program Plan Intro
NOT operation:
- NOT function needs one input and produces one output.
- It is also known as unary logical function.
- Another name of NOT operation is complementary operation.
- Output is produced by complementing the input.
- The following diagram depicts the NOT operation,
- The NOT operation produces the output “1”, when the source input is “0”.
- The NOT operation produces the output “0”, when the source input is “1”.
- The truth table for the NOT operation is as follows,
| X | |
| 0 | 1 |
| 1 | 0 |
- In the above table, “X” is the input, and “Z” is the output.
- When “X=0”, the output “Z” is the complement of “0”, which means “1” and When “X=1”,the output “Z” is the complement of “1”, which means “0”.
OR operation:
- OR function needs two inputs and produces one output.
- It is also known as binary logical function.
- If one of the inputs or both the inputs are “1”, then one-bit OR operation produces the output as “1”.
- If both the inputs are “0”, then OR operation produces the output “0”.
- The following diagram depicts the one-bit OR operation,
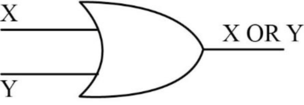
- The truth table for OR operation is as follows,
| X | Y | Z=X OR Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
- In the above table, “X” and “Y” are the inputs, and “Z” is the output.
- In the above table, when “X=0”, and “Y=0”, the output “Z” is “0”, because both the inputs “X” and “Y” contains the value “0”.
- When “X=0”, and “Y=1”, the output “Z” is “1”, because one of the input “Y” contains the value “1”.
- When “X=1”, and “Y=0”, the output “Z” is “1”, because one of the input “X” contains the value “1”.
- When “X=1”, and “Y=1”, the output “Z” is “1”, because both the inputs “X” and “Y” contains the value “1”.
AND function:
- AND function needs two inputs and produces one output.
- It is also known as binary logical function.
- If one or both the inputs are “0”, then one-bit AND operation produces the output “0”.
- If both inputs are “1”, then AND operation produces the output as “1”.
- The following diagram depicts the AND operation,
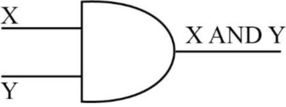
- The truth table for AND operation is as follows,
| X | Y | X AND Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
- In the above table, “X” and “Y” are inputs, and “Z” is output.
- When “X=0”, and “Y=0”, the output is “0”, because both the inputs “X” and “Y” contains the value “0”.
- When “X=0”, and “Y=1”, the output is “0”, because one of the input “X” contains the value “0”.
- When “X=1”, and “Y=0”, the output is “0”, because one of the input “Y” contains the value “0”.
- When “X=1”, and “Y=1”, the output is “1”, because both the inputs “X” and “Y” contains the value “1”.
b.
Explanation of Solution
To compute “NOT (1000 AND (1100 OR 0101))”:
- To compute “(1100 OR 0101)”,
- The OR operation can be applied on each pair of bits individually and hence it is called bit-wise OR operation.
- The OR operation for the binary numbers “1100” and “0101” is as follows,
- The output bit is “1”, when one or both of the input bits are “1” and the output bit is “0”, when both the input bits are “0”.
- The result of “(1100 OR 0101)” is “1101”.
- To compute “1000 AND (1100 OR 0101))”,
- Compute the AND operation for the binary number “1000” and the result “1101”.
- The AND operation can be applied on each pair of bits individually and hence it is called bit-wise AND operation.
- The AND operation for the given binary number is as follows,
c.
Explanation of Solution
To compute “NOT(NOT(1101))”:
- First compute “NOT (1101)”,
- The NOT operation can be applied on each bits individually and hence it is called bit-wise NOT operation.
- The NOT operation for the binary number “1101” is as follows,
- The output bit is “0”, when the input bit is “1” and the output bit is “1”, when the input bit is “0”.
- The result of the above calculation is “0010”...
d.
Explanation of Solution
To compute “(0110 OR 0000) AND 1111”:
- First compute “(0110 OR 0000)”,
- The OR operation can be applied on each pair of bits individually and hence it is called bit-wise OR operation.
- The OR operation for the given binary number is as follows,
- The output bit is “1”, when one or both of the input bits are “1” and the output bit is “0”, when both the input bits are “0”.
- The result of the above calculation is “0110”.
- Compute “0110 AND 1111”,
- The AND operation can be applied on each pair of bits individually and hence it is called bit-wise AND operation...
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
In the diagram, there is a green arrow pointing from Input C (complete data) to Transformer Encoder S_B, which I don’t understand. The teacher model is trained on full data, but S_B should instead receive missing data—this arrow should not point there. Please verify and recreate the diagram to fix this issue. Additionally, the newly created diagram should meet the same clarity standards as the second diagram (Proposed MSCATN). Finally provide the output image of the diagram in image format .
Please provide me with the output image of both of them . below are the diagrams code
make sure to update the code and mentionned clearly each section also the digram should be clearly describe like in the attached image. please do not provide the same answer like in other question . I repost this question because it does not satisfy the requirment I need in terms of clarifty the output of both code are not very well details
I have two diagram :
first diagram code
graph LR subgraph Teacher Model (Pretrained) Input_Teacher[Input C (Complete Data)] --> Teacher_Encoder[Transformer Encoder T] Teacher_Encoder --> Teacher_Prediction[Teacher Prediction y_T] Teacher_Encoder --> Teacher_Features[Internal Features F_T] end subgraph Student_A_Model[Student Model A (Handles Missing Values)] Input_Student_A[Input M (Data with Missing Values)] --> Student_A_Encoder[Transformer Encoder E_A] Student_A_Encoder --> Student_A_Prediction[Student A Prediction y_A] Student_A_Encoder…
Why I need ?
Chapter 2 Solutions
Introduction To Computing Systems
Ch. 2 - Prob. 1ECh. 2 - Prob. 2ECh. 2 - Prob. 3ECh. 2 - Prob. 4ECh. 2 - Prob. 5ECh. 2 - Prob. 6ECh. 2 - Prob. 7ECh. 2 - Prob. 8ECh. 2 - Prob. 9ECh. 2 - Prob. 10E
Ch. 2 - Prob. 11ECh. 2 - Prob. 12ECh. 2 - Prob. 13ECh. 2 - Prob. 14ECh. 2 - Prob. 15ECh. 2 - Prob. 17ECh. 2 - Prob. 18ECh. 2 - Prob. 19ECh. 2 - Prob. 20ECh. 2 - Prob. 21ECh. 2 - Prob. 22ECh. 2 - Prob. 23ECh. 2 - Prob. 24ECh. 2 - Prob. 25ECh. 2 - Prob. 26ECh. 2 - Prob. 27ECh. 2 - When is the output of an AND operation equal to...Ch. 2 - Prob. 29ECh. 2 - Prob. 30ECh. 2 - When is the output of an OR operation equal to 1?
Ch. 2 - Prob. 32ECh. 2 - Prob. 33ECh. 2 - Prob. 34ECh. 2 - Prob. 35ECh. 2 - Prob. 36ECh. 2 - Prob. 37ECh. 2 - Prob. 38ECh. 2 - Prob. 39ECh. 2 - Prob. 40ECh. 2 - Prob. 41ECh. 2 - A computer programmer wrote a program that adds...Ch. 2 - Prob. 43ECh. 2 - Prob. 44ECh. 2 - Prob. 45ECh. 2 - Prob. 46ECh. 2 - Prob. 47ECh. 2 - Prob. 48ECh. 2 - Prob. 49ECh. 2 - Prob. 50ECh. 2 - Prob. 51ECh. 2 - Prob. 52ECh. 2 - Prob. 53ECh. 2 - Fill in the truth table for the equations given....Ch. 2 - Prob. 55ECh. 2 - Prob. 56E
Knowledge Booster
Similar questions
- Here are two diagrams. Make them very explicit, similar to Example Diagram 3 (the Architecture of MSCTNN). graph LR subgraph Teacher_Model_B [Teacher Model (Pretrained)] Input_Teacher_B[Input C (Complete Data)] --> Teacher_Encoder_B[Transformer Encoder T] Teacher_Encoder_B --> Teacher_Prediction_B[Teacher Prediction y_T] Teacher_Encoder_B --> Teacher_Features_B[Internal Features F_T] end subgraph Student_B_Model [Student Model B (Handles Missing Labels)] Input_Student_B[Input C (Complete Data)] --> Student_B_Encoder[Transformer Encoder E_B] Student_B_Encoder --> Student_B_Prediction[Student B Prediction y_B] end subgraph Knowledge_Distillation_B [Knowledge Distillation (Student B)] Teacher_Prediction_B -- Logits Distillation Loss (L_logits_B) --> Total_Loss_B Teacher_Features_B -- Feature Alignment Loss (L_feature_B) --> Total_Loss_B Partial_Labels_B[Partial Labels y_p] -- Prediction Loss (L_pred_B) --> Total_Loss_B Total_Loss_B -- Backpropagation -->…arrow_forwardPlease provide me with the output image of both of them . below are the diagrams code I have two diagram : first diagram code graph LR subgraph Teacher Model (Pretrained) Input_Teacher[Input C (Complete Data)] --> Teacher_Encoder[Transformer Encoder T] Teacher_Encoder --> Teacher_Prediction[Teacher Prediction y_T] Teacher_Encoder --> Teacher_Features[Internal Features F_T] end subgraph Student_A_Model[Student Model A (Handles Missing Values)] Input_Student_A[Input M (Data with Missing Values)] --> Student_A_Encoder[Transformer Encoder E_A] Student_A_Encoder --> Student_A_Prediction[Student A Prediction y_A] Student_A_Encoder --> Student_A_Features[Student A Features F_A] end subgraph Knowledge_Distillation_A [Knowledge Distillation (Student A)] Teacher_Prediction -- Logits Distillation Loss (L_logits_A) --> Total_Loss_A Teacher_Features -- Feature Alignment Loss (L_feature_A) --> Total_Loss_A Ground_Truth_A[Ground Truth y_gt] -- Prediction Loss (L_pred_A)…arrow_forwardI'm reposting my question again please make sure to avoid any copy paste from the previous answer because those answer did not satisfy or responded to the need that's why I'm asking again The knowledge distillation part is not very clear in the diagram. Please create two new diagrams by separating the two student models: First Diagram (Student A - Missing Values): Clearly illustrate the student training process. Show how knowledge distillation happens between the teacher and Student A. Explain what the teacher teaches Student A (e.g., handling missing values) and how this teaching occurs (e.g., through logits, features, or attention). Second Diagram (Student B - Missing Labels): Similarly, detail the training process for Student B. Clarify how knowledge distillation works between the teacher and Student B. Specify what the teacher teaches Student B (e.g., dealing with missing labels) and how the knowledge is transferred. Since these are two distinct challenges…arrow_forward
- The knowledge distillation part is not very clear in the diagram. Please create two new diagrams by separating the two student models: First Diagram (Student A - Missing Values): Clearly illustrate the student training process. Show how knowledge distillation happens between the teacher and Student A. Explain what the teacher teaches Student A (e.g., handling missing values) and how this teaching occurs (e.g., through logits, features, or attention). Second Diagram (Student B - Missing Labels): Similarly, detail the training process for Student B. Clarify how knowledge distillation works between the teacher and Student B. Specify what the teacher teaches Student B (e.g., dealing with missing labels) and how the knowledge is transferred. Since these are two distinct challenges (missing values vs. missing labels), they should not be combined in the same diagram. Instead, create two separate diagrams for clarity. For reference, I will attach a second image…arrow_forwardNote : please avoid using AI answer the question by carefully reading it and provide a clear and concise solutionHere is a clear background and explanation of the full method, including what each part is doing and why. Background & Motivation Missing values: Some input features (sensor channels) are missing for some samples due to sensor failure or corruption. Missing labels: Not all samples have a ground-truth RUL value. For example, data collected during normal operation is often unlabeled. Most traditional deep learning models require complete data and full labels. But in our case, both are incomplete. If we try to train a model directly, it will either fail to learn properly or discard valuable data. What We Are Doing: Overview We solve this using a Teacher–Student knowledge distillation framework: We train a Teacher model on a clean and complete dataset where both inputs and labels are available. We then use that Teacher to teach two separate Student models: Student A learns…arrow_forwardHere is a clear background and explanation of the full method, including what each part is doing and why. Background & Motivation Missing values: Some input features (sensor channels) are missing for some samples due to sensor failure or corruption. Missing labels: Not all samples have a ground-truth RUL value. For example, data collected during normal operation is often unlabeled. Most traditional deep learning models require complete data and full labels. But in our case, both are incomplete. If we try to train a model directly, it will either fail to learn properly or discard valuable data. What We Are Doing: Overview We solve this using a Teacher–Student knowledge distillation framework: We train a Teacher model on a clean and complete dataset where both inputs and labels are available. We then use that Teacher to teach two separate Student models: Student A learns from incomplete input (some sensor values missing). Student B learns from incomplete labels (RUL labels missing…arrow_forward
- here is a diagram code : graph LR subgraph Inputs [Inputs] A[Input C (Complete Data)] --> TeacherModel B[Input M (Missing Data)] --> StudentA A --> StudentB end subgraph TeacherModel [Teacher Model (Pretrained)] C[Transformer Encoder T] --> D{Teacher Prediction y_t} C --> E[Internal Features f_t] end subgraph StudentA [Student Model A (Trainable - Handles Missing Input)] F[Transformer Encoder S_A] --> G{Student A Prediction y_s^A} B --> F end subgraph StudentB [Student Model B (Trainable - Handles Missing Labels)] H[Transformer Encoder S_B] --> I{Student B Prediction y_s^B} A --> H end subgraph GroundTruth [Ground Truth RUL (Partial Labels)] J[RUL Labels] end subgraph KnowledgeDistillationA [Knowledge Distillation Block for Student A] K[Prediction Distillation Loss (y_s^A vs y_t)] L[Feature Alignment Loss (f_s^A vs f_t)] D -- Prediction Guidance --> K E -- Feature Guidance --> L G --> K F --> L J -- Supervised Guidance (if available) --> G K…arrow_forwarddetails explanation and background We solve this using a Teacher–Student knowledge distillation framework: We train a Teacher model on a clean and complete dataset where both inputs and labels are available. We then use that Teacher to teach two separate Student models: Student A learns from incomplete input (some sensor values missing). Student B learns from incomplete labels (RUL labels missing for some samples). We use knowledge distillation to guide both students, even when labels are missing. Why We Use Two Students Student A handles Missing Input Features: It receives input with some features masked out. Since it cannot see the full input, we help it by transferring internal features (feature distillation) and predictions from the teacher. Student B handles Missing RUL Labels: It receives full input but does not always have a ground-truth RUL label. We guide it using the predictions of the teacher model (prediction distillation). Using two students allows each to specialize in…arrow_forwardWe are doing a custom JSTL custom tag to make display page to access a tag handler. Write two custom tags: 1) A single tag which prints a number (from 0-99) as words. Ex: <abc:numAsWords val="32"/> --> produces: thirty-two 2) A paired tag which puts the body in a DIV with our team colors. Ex: <abc:teamColors school="gophers" reverse="true"> <p>Big game today</p> <p>Bring your lucky hat</p> <-- these will be green text on blue background </abc:teamColors> Details: The attribute for numAsWords will be just val, from 0 to 99 - spelling, etc... isn't important here. Print "twenty-six" or "Twenty six" ... . Attributes for teamColors are: school, a "required" string, and reversed, a non-required boolean. - pick any four schools. I picked gophers, cyclones, hawkeyes and cornhuskers - each school has two colors. Pick whatever seems best. For oine I picked "cyclones" and red text on a gold body - if…arrow_forward
- I want a database on MySQL to analyze blood disease analyses with a selection of all its commands, with an ER drawing, and a complete chart for normalization. I want them completely.arrow_forwardAssignment Instructions: You are tasked with developing a program to use city data from an online database and generate a city details report. 1) Create a new Project in Eclipse called "HW7". 2) Create a class "City.java" in the project and implement the UML diagram shown below and add comments to your program. 3) The logic for the method "getCityCategory" of City Class is below: a. If the population of a city is greater than 10000000, then the method returns "MEGA" b. If the population of a city is greater than 1000000 and less than 10000000, then the method returns "LARGE" c. If the population of a city is greater than 100000 and less than 1000000, then the method returns "MEDIUM" d. If the population of a city is below 100000, then the method returns "SMALL" 4) You should create another new Java program inside the project. Name the program as "xxxx_program.java”, where xxxx is your Kean username. 3) Implement the following methods inside the xxxx_program program The main method…arrow_forwardCPS 2231 - Computer Programming – Spring 2025 City Report Application - Due Date: Concepts: Classes and Objects, Reading from a file and generating report Point value: 40 points. The purpose of this project is to give students exposure to object-oriented design and programming using classes in a realistic application that involves arrays of objects and generating reports. Assignment Instructions: You are tasked with developing a program to use city data from an online database and generate a city details report. 1) Create a new Project in Eclipse called "HW7”. 2) Create a class "City.java" in the project and implement the UML diagram shown below and add comments to your program. 3) The logic for the method "getCityCategory" of City Class is below: a. If the population of a city is greater than 10000000, then the method returns "MEGA" b. If the population of a city is greater than 1000000 and less than 10000000, then the method returns "LARGE" c. If the population of a city is greater…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education
Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON
Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON
C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON
Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning
Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education