
Concept explainers
The Dieterici equation of state for one mole of gas is
Where a and b are constants determined experimentally. For NH3(g), a = 10.91 atm. L2 and b = 0.0401 L. Plot the pressure of the gas as the volume of 1.00 mol of NH3(g) expands from 22.4 L to 50.0 L at 273 K, and numerically determine the work done by the gas by measuring the area under the curve.
Interpretation:
The Dieterici equation of state for one mole of gas is
Where a and b are constants determined experimentally. For NH3(g), a = 10.91 atm. L2 and b = 0.0401 L. The pressure of the gas as the volume of 1.00 mol of NH3(g) expands from 22.4 L to 50.0 L at 273 K is to be plotted and numerically the work done by the gas by measuring the area under the curve is to be determined.
Concept introduction:
The ideal gas law considered the molecules of a gas as point particles with perfectly elastic collisions among them in nature. This works importantly well for gases at dilution and at low pressure in many experimental calculations. But the gas molecules are not performing as point masses, and there are situations where the properties of the gas molecules have measurable effect by experiments. Thus, a modification of the ideal gas equation was coined by Johannes D. van der Waals in 1873 to consider size of molecules and the interaction forces among them. Berthelot modified the van der Waals equation as modified Berthelot model of state and further changes was made, and the equation was provided as Dieterici equation of state. The significant advantages of this equation, such as a more realistic critical compressibility factor are documented.
Answer to Problem 2.91E
The Dieterici equation of state for one mole of gas is
Explanation of Solution
The Dieterici equation of state for one mole of gas is
Given,
a = 10.91 atm. L2
b = 0.0401 L
volume of gas initial = 22.4 L
volume of gas final = 50.0 L
temperature of system = 273 K
pressure at 22.4 L is calculated as,
∴ pressure at 22.4 L = 0.9794 atm
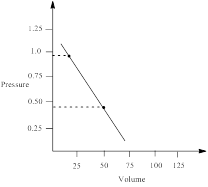
Similarly, pressure at 50 L is calculated as follows;
∴ pressure at 50 L = 0.4435 atm
From the graph the pressure difference can be calculated as;
0.5359 atm.
the work done by the gas by measuring the area under the curve is determined as;
Thus, the pressure of the gas is plotted against volume and the work done in expansion is calculated.
Want to see more full solutions like this?
Chapter 2 Solutions
Physical Chemistry
- Indicate the formula of the product obtained by reacting methyl 5-chloro-5-oxopentanoate with 1 mole of 4-penten-1-ylmagnesium bromide.arrow_forwardIn the two chair conformations of glucose, the most stable is the one with all the OH groups in the equatorial position. Is this correct?arrow_forwardIndicate the formula of the product obtained by reacting D-Galactose with hydroxylamine.arrow_forward
- helparrow_forwardThe temperature on a sample of pure X held at 1.25 atm and -54. °C is increased until the sample boils. The temperature is then held constant and the pressure is decreased by 0.42 atm. On the phase diagram below draw a path that shows this set of changes. pressure (atm) 2 0 0 200 400 temperature (K) Xarrow_forwardQUESTION: Answer Question 5: 'Calculating standard error of regression' STEP 1 by filling in all the empty green boxes *The values are all provided in the photo attached*arrow_forward
 Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning Introduction to General, Organic and BiochemistryChemistryISBN:9781285869759Author:Frederick A. Bettelheim, William H. Brown, Mary K. Campbell, Shawn O. Farrell, Omar TorresPublisher:Cengage Learning
Introduction to General, Organic and BiochemistryChemistryISBN:9781285869759Author:Frederick A. Bettelheim, William H. Brown, Mary K. Campbell, Shawn O. Farrell, Omar TorresPublisher:Cengage Learning Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,
Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning, Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning





