
Concept explainers
(a)
Show that in case of heavy damping
(a)
Explanation of Solution
Calculation:
Since
The expression for the differential equation of over damping as follows:
Differentiate the above equation with respect to ‘t’.
Since the body is released with no initial velocity.
Substitute 0 for t,
Substitute 0 for t,
Substitute
Substitute
Substitute
Apply boundary condition.
For
As
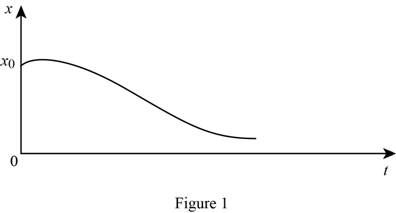
Thus the positive answer for the ‘t’ greater than 0 for the equation (4) cannot exist because the exponential (e) is increased to positive power be less than one which is not possible. Hence, the value of x is not becomes zero.
Show the graph of x versus t for the above solution as Figure (1).
(b)
Show that in case of heavy damping
(b)
Explanation of Solution
Calculation:
Since the body is started from O with arbitrary initial velocity.
Substitute 0 for t, 0 for x and
Substitute 0 for t, 0 for x, and
Substitute
Substitute
Substitute
Apply boundary condition.
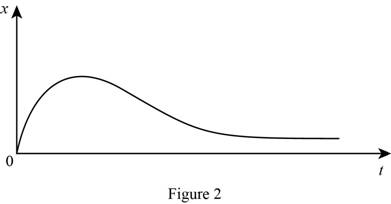
For
For
Show the graph of x versus t for the above solution as Figure (2).
Want to see more full solutions like this?
Chapter 19 Solutions
VECTOR MECH...,STAT.+DYNA.(LL)-W/ACCESS
- Find the componenets of reactions at pins of A, B and D please show the detailed process and instructions for learning draw out all diagrams please and thank youarrow_forwardA cast iron cylinder of 200 mm inner diameter and 12.5 mm thick is closely wound with a layer of 4 mm diameter steel wire under a tensile stress of 55 MN/m². Determine the stresses set up in the cylinder and steel wire if water under a pressure of 3 MN/m² is admitted in the cylinder. Take E= 100 GN/m², E = 200 GN/m² and Poisson's ratio = 0.25.arrow_forwardWhat is the effect of a clogged fuel injector?arrow_forward
- You are asked to design a unit to condense ammonia. The required condensation rate is 0.09kg/s. Saturated ammonia at 30 o C is passed over a vertical plate (10 cm high and 25 cm wide).The properties of ammonia at the saturation temperature of 30°C are hfg = 1144 ́10^3 J/kg andrho_v = 9.055 kg/m 3 . Use the properties of liquid ammonia at the film temperature of 20°C (Ts =10 o C):Pr = 1.463 rho_l= 610.2 kf/m^3 liquid viscosity= 1.519*10^-4 kg/ ms kinematic viscosity= 2.489*10^-7 m^2/s Cpl= 4745 J/kg C kl=0.4927 W/m C hfg*=hfg+0.68Cpl(Tsat-Given Ts) a) Instead of one plate you want to use small plates and install many of them. Calculate the requiredsurface temperature to achieve the desired condensation rate (0.09 kg/s) if you install 36vertical plates (with the same dimension as above: 10 cm high and 25 cm wide).arrow_forward11-19 designed in Problem The shaft shown in figure P11-4 was 10-19, for the data in the row(s) assigned from table PII-1, and the corresponding diameter of shaft found in Problem 10-19, design suitable bearings 5 E8 cycles at the load for at least State all assumptions. to support 1200rpm. (a) Using hydrodynamically lubricated bronze sleeve bearings with ON = 40, Lld = 0.8, and clearance ratio 0.0025. of a ← gear T gear Key figure PI-4 Given from the problem 10-19 we get d= 1.153 in from the table 11-1 we get a = 16 in b= 18in L= 20inarrow_forwardIn an irrigation system, the following characteristics of the pipe network are available.• 100 meters of 4" PVC pipe, 3 gate valves• 500 meters of 3" PVC pipe, 4 gate valves• 200 meters of 2" H.G. pipe, 2 globe valves• 50 litres per second circulate in the pipes:Calculate:1. Total energy losses in meters.2. Leaks in pipes.3. Losses in accessories.4. Calculate the equivalent pipe of that system assuming only pipes without fittings.Solve the problem without artificial intelligence, solve by one of the expertsarrow_forward
- In a series pipe, calculate the diameter 2 according to the following:• Ltotal: 325 m• L1: 52 m, D1: 3/4"• L2: 254 m, D2:?• L3: 19 m, D: 1-1/4".Indicate the nominal diameter. Solve without using artificial inteligence, solve by one of the expertsarrow_forwardWhat is the critical speed of the shaft in rad/s for one, two, and three elements?arrow_forward2. Express the following complex numbers in rectangular form. (a) z₁ = 2еjл/6 (b) Z2=-3e-jπ/4 (c) Z3 = √√√3e-j³/4 (d) z4 = − j³arrow_forward
- A prismatic beam is built into a structure. You can consider the boundary conditions at A and B to be fixed supports. The beam was originally designed to withstand a triangular distributed load, however, the loading condition has been revised and can be approximated by a cosine function as shown in the figure below. You have been tasked with analysing the structure. As the beam is prismatic, you can assume that the bending rigidity (El) is constant. wwo cos 2L x A B Figure 3: Built in beam with a varying distributed load In order to do this, you will: a. Solve the reaction forces and moments at point A and B. Hint: you may find it convenient to use the principal of superposition. (2%) b. Plot the shear force and bending moment diagrams and identify the maximum shear force and bending moment. (2%) c. Develop an expression for the vertical deflection. Clearly state your expression in terms of x. (1%)arrow_forwardQuestion 1: Beam Analysis Two beams (ABC and CD) are connected using a pin immediately to the left of Point C. The pin acts as a moment release, i.e. no moments are transferred through this pinned connection. Shear forces can be transferred through the pinned connection. Beam ABC has a pinned support at point A and a roller support at Point C. Beam CD has a roller support at Point D. A concentrated load, P, is applied to the mid span of beam CD, and acts at an angle as shown below. Two concentrated moments, MB and Mc act in the directions shown at Point B and Point C respectively. The magnitude of these moments is PL. Moment Release A B с ° MB = PL Mc= = PL -L/2- -L/2- → P D Figure 1: Two beam arrangement for question 1. To analyse this structure, you will: a) Construct the free body diagrams for the structure shown above. When constructing your FBD's you must make section cuts at point B and C. You can represent the structure as three separate beams. Following this, construct the…arrow_forwardA cantilevered rectangular prismatic beam has three loads applied. 10,000N in the positive x direction, 500N in the positive z direction and 750 in the negative y direction. You have been tasked with analysing the stresses at three points on the beam, a, b and c. 32mm 60mm 24mm 180mm 15mm 15mm 40mm 750N 16mm 500N x 10,000N Figure 2: Idealisation of the structure and the applied loading (right). Photograph of the new product (left). Picture sourced from amazon.com.au. To assess the design, you will: a) Determine state of stress at all points (a, b and c). These points are located on the exterior surface of the beam. Point a is located along the centreline of the beam, point b is 15mm from the centreline and point c is located on the edge of the beam. When calculating the stresses you must consider the stresses due to bending and transverse shear. Present your results in a table and ensure that your sign convention is clearly shown (and applied consistently!) (3%) b) You have identified…arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





