
Concept explainers
A small collar of mass 1 kg is rigidly attached to a 3-kg uniform rod of length L = 750 mm. Determine (a) the distance d to maximize the frequency of oscillation when the rod is given a small initial displacement, (b) the corresponding period of oscillation.
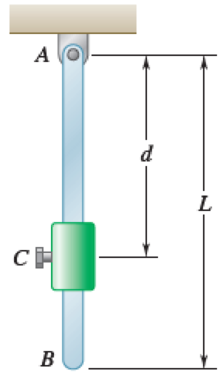
Fig. P19.50
(a)
The distance d to maximize the frequency of oscillation when the rod is given a small initial displacement.
Answer to Problem 19.50P
The distance d to maximize the frequency of oscillation when the rod is given a small initial displacement is
Explanation of Solution
Given information:
The mass
The mass
The length (L) of the rod AB is 750 mm.
The acceleration due to gravity (g) is
Calculation:
Show the free-body-diagram equation as in Figure (1).
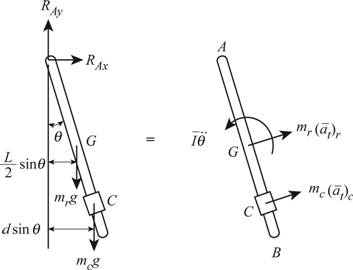
The external forces in the system are forces due mass of the collar and the rod. The effective force in the system is
Take moment about A in the system for external forces.
For small oscillation
Take moment about A in the system for effective forces.
The tangential component of acceleration for the rod
The tangential component of acceleration for the collar
Thus, express the moment about A due to the effective forces as:
Equate the moment about A in the system for external and effective forces.
Compare the differential Equation (1) with the general differential equation of motion
Write the expression for moment of inertia of the rod:
Substitute 1 kg for
Calculate the value of d to maximize the natural frequency:
Differentiate Equation (3) with respect to d.
Equate
Solve the above quadratic equation:
Express the roots of a quadratic equation:
Substitute d for x, 1 for a, 2.25 for b, and -0.5625 for c to find the roots of the Equation (4).
Therefore, the distance d to maximize the frequency of oscillation when the rod is given a small initial displacement is
(b)
The corresponding period
Answer to Problem 19.50P
The corresponding period
Explanation of Solution
Given information:
The mass
The mass
The length (L) of the rod AB is 750 mm.
The acceleration due to gravity (g) is
Calculation:
Calculate the value of maximum natural circular frequency
Substitute 0.227 m for d in Equation (3)
Calculate the time period of oscillation
Substitute
Therefore, the corresponding period
Want to see more full solutions like this?
Chapter 19 Solutions
VECTOR MECH...,STAT.+DYNA.(LL)-W/ACCESS
- A torque of magnitude T = 12 kNm is applied to the end of a tank containing compressed air under a pressure of 8 MPa (Figure Q1). The tank has a 180 mm inner diameter and a 12 mm wall thickness. As a result of several tensile tests, it has been found that tensile yeild strength is σy = 250 MPa for thr grade of steel used. Determine the factor of safety with respect to yeild, using: (a) The maximum shearing stress theory (b) The maximum distortion energy theory T Figure Q1arrow_forwardAn external pressure of 12 MPa is applied to a closed-end thick cylinder of internal diameter 150 mm and external diameter 300 mm. If the maximum hoop stress on the inner surface of the cylinder is limited to 30 MPa: (a) What maximum internal pressure can be applied to the cylinder? (b) Sketch the variation of hoop and radial stresses across the cylinder wall. (c) What will be the change in the outside diameter when the above pressure is applied? [Take E = 207 GPa and v = 0.29]arrow_forwardso A 4 I need a detailed drawing with explanation し i need drawing in solution motion is as follows; 1- Dwell 45°. Plot the displacement diagram for a cam with flat follower of width 14 mm. The required 2- Rising 60 mm in 90° with Simple Harmonic Motion. 3- Dwell 90°. 4- Falling 60 mm for 90° with Simple Harmonic Motion. 5- Dwell 45°. cam is 50 mm. Then design the cam profile to give the above displacement diagram if the minimum circle diameter of the か ---2-125 750 x2.01 98Parrow_forward
- Figure below shows a link mechanism in which the link OA rotates uniformly in an anticlockwise direction at 10 rad/s. the lengths of the various links are OA=75 mm, OB-150 mm, BC=150 mm, CD-300 mm. Determine for the position shown, the sliding velocity of D. A 45 B Space Diagram o NTS (Not-to-Scale) C Darrow_forwardI need a detailed drawing with explanation so Solle 4 يكا Pax Pu + 96** motion is as follows; 1- Dwell 45°. Plot the displacement diagram for a cam with flat follower of width 14 mm. The required 2- Rising 60 mm in 90° with Simple Harmonic Motion. 3- Dwell 90°. 4- Falling 60 mm for 90° with Simple Harmonic Motion. 5- Dwell 45°. cam is 50 mm. Then design the cam profile to give the above displacement diagram if the minimum circle diameter of the 55 ---20125 750 X 2.01 1989arrow_forwardAshaft fitted with a flywheel rotates at 300 rpm. and drives a machine. The torque required to drive the machine varies in a cyclic manner over a period of 2 revolutions. The torque drops from 20,000 Nm to 10,000 Nm uniformly during 90 degrees and remains constant for the following 180 degrees. It then rises uniformly to 35,000 Nm during the next 225 degrees and after that it drops to 20,000 in a uniform manner for 225 degrees, the cycle being repeated thereafter. Determine the power required to drive the machine and percentage fluctuation in speed, if the driving torque applied to the shaft is constant and the mass of the flywheel is 12 tonnes with radius of gyration of 500 mm. What is the maximum angular acceleration of the flywheel. 35,000 TNM 20,000 10,000 0 90 270 495 Crank angle 8 degrees 720arrow_forward
- chanism shown in figure below, the crank OA rotates at 60 RPM counterclockwise. The velocity diagram is also drawn to scale (take dimensions from space diagram). Knowing that QCD is rigid plate, determine: a. Linear acceleration of slider at B, b. Angular acceleration of the links AC, plate CQD, and BD. D Space Diagram Scale 1:10 A ES a o,p,g b Velocity Diagram Scale 50 mm/(m/s) darrow_forwardA thick closed cylinder, 100 mm inner diameter and 200 mm outer diameter is subjected to an internal pressure of 230 MPa and outer pressure of 70 MPa. Modulus of elasticity, E=200 GPa. and Poisson's ratio is 0.3, determine: i) The maximum hoop stress ii) The maximum shear stress iii) The new dimension of the outer diameter due to these inner and outer pressures.arrow_forwardA ә レ shaft fitted with a flywheel rotates at 300 rpm. and drives a machine. The torque required to drive the machine varies in a cyclic manner over a period of 2 revolutions. The torque drops from 20,000 Nm to 10,000 Nm uniformly during 90 degrees and remains constant for the following 180 degrees. It then rises uniformly to 35,000 Nm during the next 225 degrees and after that it drops to 20,000 in a uniform manner for 225 degrees, the cycle being repeated thereafter. Determine the power required to drive the machine and percentage fluctuation in speed, if the driving torque applied to the shaft is constant and the mass of the flywheel is 12 tonnes with radius of gyration of 500 mm. What is the maximum angular acceleration of the flywheel. 35,000 TNm 20,000 10,000 495 Crank angle 8 degrees 270 0 90 か ---20125 750 X 2.01 44 720 sarrow_forward
- The gas tank is made from A-36 steel (σy = 250 MPa) and has an inner diameter of 3.50 m. If the tank is designed to withstand a pressure of 1.2 MPa, determine the required minimum wall thickness to the nearest millimeter using (a) The maximum-shear-stress theory (b) Maximum distortion- energy theory. Apply a factor of safety of 1.5 against yielding.arrow_forwardә レ Figure below shows a link mechanism in which the link OA rotates uniformly in an anticlockwise direction at 10 rad/s. the lengths of the various links are OA=75 mm, OB-150 mm, BC=150 mm, CD-300 mm. Determine for the position shown, the sliding velocity of D. A A B # Space Diagram o NTS (Not-to-Scale) C 10 =--20125 735) 750 x2.01 اهarrow_forward2 レ Tanism in which the link OA mm. O anticlockwise direction at 10 rad/s, the lengths of the various links are OA=75mm, OB=150mm, BC=150mm,CD=300mm. Determine for the position shown, the sliding velocity of D. A A Space Diagram o NT$ (Not-to-Scale) B # C か 750 x2.01 165 79622arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





