
Concept explainers
A 2.5-kg homogeneous disk of radius 80 mm rotates with an angular velocity ω1 with respect to arm ABC, which is welded to a shaft DCE rotating as shown at the constant rate ω2 = 12 rad/s. Friction in the bearing at A causes ω1 to decrease at the rate of 15 rad/s2. Determine the dynamic reactions at D and E at a time when ω1 has decreased to 50 rad/s.
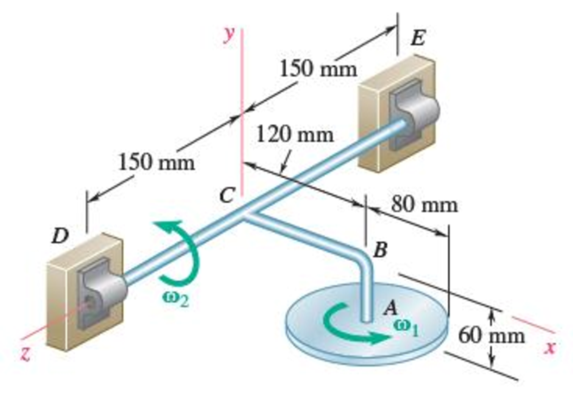
Fig. P18.103 and P18.104
The dynamic reactions at D and E at a time when
Answer to Problem 18.103P
The dynamic reactions at Dat a time when
The dynamic reactions at Eat a time when
Explanation of Solution
Given information:
The mass (m) of the disk is 2.5kg.
The radius (r) of the disk Ais 80 mm.
The angular velocity
The decreasing acceleration
Calculation:
The angular velocity
Write the equation of angular velocity of disk A
Write the equation of angular velocity
Find the equation of angular velocity
Substitute 0 for
Find the equation of angular momentum about A
Here,
Substitute 0 for
Find the rate of change of angular momentum
Here,
Write the equation of vector form of angular velocity
Write the equation of the rate of change of angular momentum about A
Substitute
Write the equation mass moment of inertia
Write the equation mass moment of inertia
Substitute
Find the position vector
Here, b is the horizontal distance and c is the vertical distance.
Write the equation of velocity
Substitute
Write the equation of acceleration of the mass center A of the disk.
Substitute
Sketch the free body diagram and kinetic diagram of the system as shown in Figure (1).
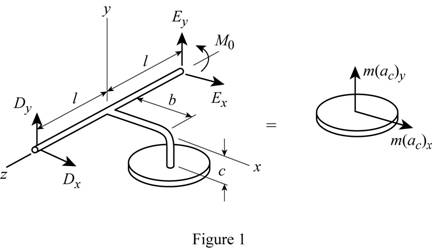
Refer Figure (1),
Apply Newton’s law of motion.
Substitute
Equate i-vector coefficients in Equation (4).
Equate j-vector coefficients in Equation (4).
Find the rate of change of angular momentum about E
Here,
Substitute
Apply matrix multiplication,
Take moment about E.
Here,
The moment at E is equal to the rate of change of angular momentum at E.
Equate Equation (7) and (8).
Convert the unit of radius from mm to m.
Convert the unit of b from mm to m.
Convert the unit of c from mm to m.
Convert the unit of l from mm to m.
Find the component of dynamic reaction
Equate
Substitute 2.5 kg for
Find the component of dynamic reaction
Equate
Substitute 2.5 kg for
Find the dynamic reaction at D using the equation:
Substitute
Thus, the dynamic reaction at D is
Find the component of dynamic reaction
Substitute Equation (11) in (5).
Substitute 2.5 kg for
Find the component of dynamic reaction
Substitute Equation (12) in (6).
Substitute 2.5 kg for
Find the dynamic reaction at E using the equation:
Substitute
Thus, the dynamic reaction at D is
Want to see more full solutions like this?
Chapter 18 Solutions
<LCPO> VECTOR MECH,STAT+DYNAMICS
- Q1: For the following force system, find the moments with respect to axes x, y, and zarrow_forwardQ10) Body A weighs 600 lb contact with smooth surfaces at D and E. Determine the tension in the cord and the forces acting on C on member BD, also calculate the reaction at B and F. Cable 6' 3' wwwarrow_forwardHelp ارجو مساعدتي في حل هذا السؤالarrow_forward
- Q3: Find the resultant of the force system.arrow_forwardQuestion 1 A three-blade propeller of a diameter of 2 m has an activity factor AF of 200 and its ratio of static thrust coefficient to static torque coefficient is 10. The propeller's integrated lift coefficient is 0.3.arrow_forward(L=6847 mm, q = 5331 N/mm, M = 1408549 N.mm, and El = 8.6 x 1014 N. mm²) X A ΕΙ B L Y Marrow_forward
- Calculate the maximum shear stress Tmax at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m. The following choices are provided in units of MPa and rounded to three decimal places. Select one: ○ 1.2681.818 O 2. 25745.455 O 3. 17163.636 O 4. 10727.273 ○ 5.5363.636arrow_forwardIf L-719.01 mm, = 7839.63 N/m³, the normal stress σ caused by self-weight at the location of the maximum normal stress in the bar can be calculated as (Please select the correct value of σ given in Pa and rounded to three decimal places.) Select one: ○ 1. 1409.193 2. 845.516 O 3. 11273.545 ○ 4.8455.159 ○ 5.4509.418 6. 2818.386 7.5636.772arrow_forwardTo calculate the rotation at Point B, a suitable virtual structure needs to be created. Which equation in the following choices most accurately represents the functional relationship between the bending moment, Mv2 ( Units: N.mm), of the virtual structure and the spatial coordinate x (Units: mm) if the applied unit virtual moment is clockwise? Select one: O 1. Mv2 1.000 O 2. Mv2=x+1.000 O 3. Mv2=x+0.000 4. Mv2 = -x-1.000 O 5. Mv2 -1.000 6. Mv2=-x+0.000arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





