
Concept explainers
Determine the kinetic energy of the space probe of Prob. 18.34 in its motion about its mass center after its collision with the meteorite.
18.34 The coordinate axes shown represent the principal centroidal axes of inertia of a 3000-lb space probe whose radii of gyration are kx = 1.375 ft, ky = 1.425 ft, and kz = 1.250 ft. The probe has no angular velocity when a 5-oz meteorite strikes one of its solar panels at point A and emerges on the other side of the panel with no change in the direction of its velocity, but with a speed reduced by 25 percent. Knowing that the final angular velocity of the probe is ω = (0.05 rad/s)i − (0.12 rad/s)j + ωzk and that the x component of the resulting change in the velocity of the mass center of the probe is −0.675 in./s, determine (a) the component ωz of the final angular velocity of the probe, (b) the relative velocity v0 with which the meteorite strikes the panel.
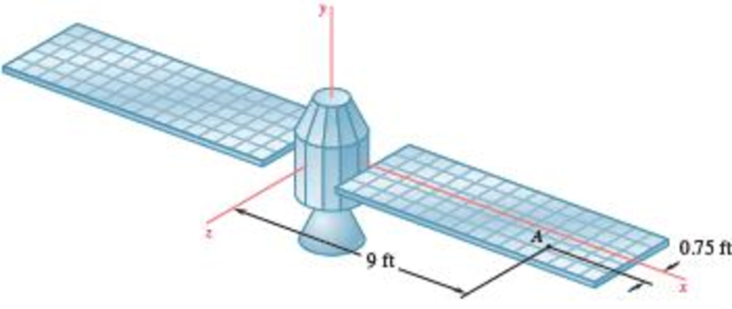
Fig. P18.33 and P18.34
The kinetic energy
Answer to Problem 18.54P
The kinetic energy
Explanation of Solution
Given information:
The weight of the space probe
The radius of gyration along x axis
The radius of gyration along y axis
The radius of gyration along z axis
The weight of the meteorite (w) is 5 oz.
The angular velocity
The change in velocity of the mass center of the probe
The width of the side panel from center to point A (b) is 9 ft.
The length of the panel from center to point A (l) is 0.75 ft.
The speed is reduced by 25 percent.
Calculation:
Calculate the mass of the space probe
Here, g is the acceleration due to gravity.
Substitute
Calculate the mass of the meteorite (m) using the formula:
Substitute
Write the relative position vector
Substitute 9 ft for b and 0.75 ft.
Write the expression for the velocity
Calculate the initial liner momentum of the meteorite using the relation:
Substitute
Calculate the moment about origin
Substitute
The speed is reduced to 25 percent.
Calculate the final liner momentum of the meteorite using the relation:
Substitute
Calculate the final linear momentum of meteorite and its moment about the origin using the relation:
Substitute
The initial linear momentum of the space probe
Calculate the final linear momentum of the space probe using the relation:
Substitute
Substitute -0.675 in./s for
Calculate the final angular momentum of the space probe
Substitute
Write the expression for the conservation of linear momentum of the probe plus the meteorite as follows:
Substitute
Equate the i component from the Equation (1).
Equate j component from the Equation (1).
Equate k component from the Equation (1).
Write the expression for the conservation of angular momentum about the origin as follows:
Substitute
Equate i component from the equation (2).
Equate k component from the equation (2).
Substitute –4840 ft/s for
Calculate the kinetic energy of motion of the probe relative to its mass center
Substitute
Thus, the kinetic energy
Want to see more full solutions like this?
Chapter 18 Solutions
<LCPO> VECTOR MECH,STAT+DYNAMICS
- (b) A steel 'hot rolled structural hollow section' column of length 5.75 m, has the cross-section shown in Figure Q.5(b) and supports a load of 750 kN. During service, it is subjected to axial compression loading where one end of the column is effectively restrained in position and direction (fixed) and the other is effectively held in position but not in direction (pinned). i) Given that the steel has a design strength of 275 MN/m², determine the load factor for the structural member based upon the BS5950 design approach using Datasheet Q.5(b). [11] ii) Determine the axial load that can be supported by the column using the Rankine-Gordon formula, given that the yield strength of the material is 280 MN/m² and the constant *a* is 1/30000. [6] 300 600 2-300 mm wide x 5 mm thick plates. Figure Q.5(b) L=5.75m Pinned Fixedarrow_forwardHelp ارجو مساعدتي في حل هذا السؤالarrow_forwardHelp ارجو مساعدتي في حل هذا السؤالarrow_forward
- Q2: For the following figure, find the reactions of the system. The specific weight of the plate is 500 lb/ft³arrow_forwardQ1: For the following force system, find the moments with respect to axes x, y, and zarrow_forwardQ10) Body A weighs 600 lb contact with smooth surfaces at D and E. Determine the tension in the cord and the forces acting on C on member BD, also calculate the reaction at B and F. Cable 6' 3' wwwarrow_forward
- Help ارجو مساعدتي في حل هذا السؤالarrow_forwardQ3: Find the resultant of the force system.arrow_forwardQuestion 1 A three-blade propeller of a diameter of 2 m has an activity factor AF of 200 and its ratio of static thrust coefficient to static torque coefficient is 10. The propeller's integrated lift coefficient is 0.3.arrow_forward
- (L=6847 mm, q = 5331 N/mm, M = 1408549 N.mm, and El = 8.6 x 1014 N. mm²) X A ΕΙ B L Y Marrow_forwardCalculate the maximum shear stress Tmax at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m. The following choices are provided in units of MPa and rounded to three decimal places. Select one: ○ 1.2681.818 O 2. 25745.455 O 3. 17163.636 O 4. 10727.273 ○ 5.5363.636arrow_forwardIf L-719.01 mm, = 7839.63 N/m³, the normal stress σ caused by self-weight at the location of the maximum normal stress in the bar can be calculated as (Please select the correct value of σ given in Pa and rounded to three decimal places.) Select one: ○ 1. 1409.193 2. 845.516 O 3. 11273.545 ○ 4.8455.159 ○ 5.4509.418 6. 2818.386 7.5636.772arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





