
Concept explainers
The dynamic reaction at D (D) and E (E).
Answer to Problem 18.153RP
The dynamic reaction at D (D) and E (E) are
Explanation of Solution
Given Information:
The weight of the disk (W) is 6 lb.
The constant angular velocity
The constant angular velocity
The radius (r) of the disk is
The length (l) of the rod is
The length of the rod from disk to point B (b) and B to C (c) is
Assume the acceleration due to gravity (g) as
Calculation:
Write the expression for the angular velocity
Write the expression for the angular velocity
Write the expression the centroidal moment of inertia
Write the expression the centroidal moment of inertia
Write the express the angular moment
Substitute
Let the reference frame Oxyz be rotating with angular velocity
Write the express the angular momentum
Substitute
Write the express the rate of change of angular
Substitute
Write the expression for the position vector
Write the expression for the velocity
Substitute
Write the expression for the acceleration
Substitute
Show the impulse momentum diagram as in Figure (1).

Write the expression for the sum of the forces:
Substitute
Resolve the i and k component,
Express the moment about the point D.
Write the expression for the position vector
Write the expression for the sum of the moment about D:
Substitute
Resolve the component i, j and k component.
For i component,
For j component,
For k component,
Calculate the mass of the disk (m) using the relation:
Substitute 6lb for W and
Differentiate the angular velocity of
Differentiate the angular velocity of
Calculate the z component dynamic reaction
Substitute 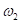 ,
,
Calculate the y component dynamic reaction
Substitute
Calculate the y component dynamic reaction
Substitute
Calculate the z component dynamic reaction
Substitute
Calculate the dynamic reaction (D) at D:
Substitute
Calculate the dynamic reaction (E) at E:
Substitute
Thus, the dynamic reaction at D (D) and E (E) are
Want to see more full solutions like this?
Chapter 18 Solutions
VECTOR MECH...,STAT.+DYN.(LL)-W/ACCESS
- In using the bolt cutter shown, a worker applies two forces P to the handles. If the magnitude ofP is 500 N, determine the magnitude of the forces exerted by the cutter on the boltarrow_forwardArterioles bifurcate (i.e., split) into capillaries in the circulatory system. Blood flows at a velocity of 20 cm/s through an arteriole with a diameter of 0.20 cm. This vessel bifurcates into two vessels: one with a diameter of 0.17 cm and a blood flow velocity of 18 cm/sec, and one with a diameter of 0.15 cm. Each of these two vessels splits again. The 0.17-cm diameter vessel splits into two vessels, each with a diameter of 0.15 cm. The 0.15-cm diameter vessel splits into two vessels, each with a diameter of 0.12 cm. Determine the mass flow rate and velocity of blood in each of the four vessels at the end of the arteriole bifurcations. You may need to set up several systems, each with a different system boundary, in order to solve this problem.arrow_forward6) Draw a Front, side and Top view for the following objects: p.s. you don't need to label the alphabet ISOMETRIC PICTORIAL VIEW K R C B E R D 0 Aarrow_forward
- Please draw the front top and side view for the following objectarrow_forwardDraw the top viewarrow_forwardSuppose that a steel of eutectoid composition is cooled to 675°C (1250°F) from 760°C (1400°F) in less than 0.5 s and held at this temperature. (a) How long will it take for the austenite-topearlite reaction to go to 50% completion? To 100% completion? (b) Estimate the hardness of the alloy that has completely transformed to pearlite.arrow_forward
- Problem 2: Determine the components of the reaction at point B (Please use paper sheet + FBD ,don't use chatgpt) MECHANICAL ENGGarrow_forwardARL040_AE_Kn_2of3... Dor Question 4. A two-throw crankshaft has masses distributed as shown: RAH 90 rpm A TRAV B Re Rev M₁ = 15kg; M₂ = 12kg L = 950mm; 1, 350mm; 1₁ = 600mm; 0₁ = 90°; 02=0°; r₁ = 300mm; r250mm The crankshaft is to be balanced by attaching masses at radii of 300 mm and rotating in planes 150 mm outside the planes of number one and number two cranks. Determine the magnitude and angular position of the balance masses. Answer 4.arrow_forwardFEAarrow_forward
- Finite Element Analysisarrow_forwardan experimental research station is constructed on a concrete slab floor. The heat loss from the floor slab is significant, given the cold environment, and is measured to be 5 kW. The edges of the floor slab are insulated with a 60 mm thickness of cellular glass insulation. The width of this insulation at the floor slab is 0.9 m. To avoid excessive fuel consumption, the station air temperature is maintained at a slightly cool temperature of 18ºC. The station is constructed in a square shape, to keep the surface area to volume ratio low; the horizontal dimensions of the floor of the station are 20 m by 20 m. The number of occupants in the research station varies between 5 and 20, depending on the research workload.a) Determine the design outdoor temperature that was used in designing the research station.b) If the floor dimensions of the station are changed to 15 m by 25 m, would the design outdoor temperature that was used in designing the research station from part (a) change? If so,…arrow_forwardFinite element analysisarrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





