Chapter 17, Problem 39P

To determine

Find the current through the inductor $i_o\left(t\right)$ of the circuit shown in Figure 17.75(b).

Answer to Problem 39P

The current through the inductor $i_o\left(t\right)$ is

$i_o\left(t\right)=\left[\frac{1}{10}+\frac{400}{\pi }{\displaystyle \sum _{k=1}^{\infty }{I}_n\sin \left(n\pi t-{\varphi }_n\right)}\right]\text{A,}n=2k-1$.

Explanation of Solution

Given data:

Refer to Figure 17.75(a) and 17.75(b) in the textbook.

The inductor L is $100\text{mH}$.

The capacitor $C$ is $50\text{mF}$.

Formula used:

Write the general expression for Fourier series expansion.

$f\left(t\right)=a_0+{\displaystyle \sum _{n=1}^{\infty }{a}_n}\cos n{\omega }_{0}t+{\displaystyle \sum _{n=1}^{\infty }{b}_n}\sin n{\omega }_{0}t$        (1)

Write the expression to calculate the fundamental angular frequency.

${\omega }_0=\frac{2\pi }{T}$        (2)

Here,

$T$ is the period of the function.

Calculation:

Refer to Figure 17.73(a) in the textbook.

The source voltage $v_s\left(t\right)$ over the period is,

$f\left(t\right)=\{\begin{array}{l}15,0<t<1\\ 5,1<t<2\end{array}$        (3)

The time period of Figure 17.75(a) is,

$T=2$

Substitute 2 for T in equation (2) to find the angular frequency ${\omega }_0$.

$\begin{array}{c}{\omega }_0=\frac{2\pi }{2}\\ =\pi \end{array}$

Finding the Fourier coefficient $a_0$.

$a_0=\frac{1}{T}{\displaystyle {\int }_0^T{v}_s\left(t\right)}dt$        (4)

Applying equation (3) in equation (4) as follows,

$\begin{array}{c}{a}_0=\frac{1}{2}\left[{\displaystyle {\int }_0^{1}15}dt+{\displaystyle {\int }_1^{2}5dt}\right]\left\{\because T=2\right\}\\ =\frac{1}{2}\left[15{\left[t\right]}_0^1+5{\left[t\right]}_1^2\right]\\ =\frac{1}{2}\left[15\left[1-0\right]+5\left[2-1\right]\right]\\ =\frac{1}{2}\left[15+5\right]\end{array}$

The above equation becomes,

$a_0=10$

Finding the Fourier coefficient $a_n$.

$a_n=\frac{2}{T}{\displaystyle {\int }_0^T{v}_s\left(t\right)\cos n{\omega }_{0}t}dt$        (5)

Applying equation (3) in equation (5) as follows,

$\begin{array}{c}{a}_n=\frac{2}{2}\left[{\displaystyle {\int }_0^1\left(15\right)\cos n\pi t}dt+{\displaystyle {\int }_1^2\left(5\right)\cos n\pi tdt}\right]\left\{\because T=2,{\omega }_0=\pi \right\}\\ =15{\left[\frac{\sin n\pi t}{n\pi }\right]}_0^1+5{\left[\frac{\sin n\pi t}{n\pi }\right]}_1^2\\ =\frac{15}{n\pi }\left[\sin n\pi \left(1\right)-0\right]+\frac{5}{n\pi }\left[\sin n\pi \left(2\right)-\sin n\pi \left(1\right)\right]\\ =0\left\{\because \sin \left(n\pi \right)=0,\sin \left(2n\pi \right)=0\right\}\end{array}$

Finding the Fourier coefficient $b_n$.

$b_n=\frac{2}{T}{\displaystyle {\int }_0^T{v}_s\left(t\right)\sin n{\omega }_{0}t}dt$        (6)

Applying equation (3) in equation (6) as follows,

$\begin{array}{c}{b}_n=\frac{2}{2}\left[{\displaystyle {\int }_0^1\left(15\right)\sin n\pi t}dt+{\displaystyle {\int }_1^2\left(5\right)\sin n\pi tdt}\right]\left\{\because T=2,{\omega }_0=\pi \right\}\\ =15{\left[\frac{-\cos n\pi t}{n\pi }\right]}_0^1+5{\left[\frac{-\cos n\pi t}{n\pi }\right]}_1^2\\ =\frac{-15}{n\pi }\left[\cos n\pi -\cos n\pi \left(0\right)\right]-\frac{5}{n\pi }\left[\cos n\pi \left(2\right)-\cos n\pi \left(1\right)\right]\\ =\frac{-15}{n\pi }\left[{\left(-1\right)}^n-1\right]-\frac{5}{n\pi }\left[1-{\left(-1\right)}^n\right]\left\{\begin{array}{l}\because \cos \left(0\right)=1,\cos \left(2n\pi \right)=1,\\ \cos n\pi ={\left(-1\right)}^n\end{array}\right\}\end{array}$

Simplify the equation as follows,

$\begin{array}{c}{b}_n=\frac{15}{n\pi }\left[1-{\left(-1\right)}^n\right]-\frac{5}{n\pi }\left[1-{\left(-1\right)}^n\right]\\ =\left[1-{\left(-1\right)}^n\right]\left[\frac{15}{n\pi }-\frac{5}{n\pi }\right]\\ =\left[1-{\left(-1\right)}^n\right]\left[\frac{10}{n\pi }\right]\end{array}$

The above equation becomes,

$b_n=\{\begin{array}{l}\frac{20}{n\pi },n=\text{odd}\\ \text{0,}n=\text{even}\end{array}$        (7)

Substituting the Fourier coefficients in equation (1) as follows,

$v_s\left(t\right)=10+{\displaystyle \sum _{n=1}^{\infty }\left(0\right)}\cos n{\omega }_{0}t+\frac{20}{\pi }{\displaystyle \sum _{k=1}^{\infty }\frac{1}{n}}\sin \left(n\pi t\right),n=2k-1\left\{{\omega }_0=\pi \right\}$

$v_s\left(t\right)=10+\frac{20}{\pi }{\displaystyle \sum _{k=1}^{\infty }\frac{1}{n}}\sin \left(n\pi t\right),n=2k-1$        (8)

Refer to Figure 17.75(b) in the textbook.

For the DC component, the current $i_o$ is,

$\begin{array}{c}{i}_o=\frac{10}{20+40}\\ =\frac{10}{60}\\ =\frac{1}{6}\text{A}\end{array}$

The inductor acts as a short circuit for DC.

For the kth harmonic,

$V_s=\frac{20}{n\pi }\angle 0°$        (9)

Consider Figure 17.75(b) for AC analysis.

The impedance of the inductor is calculated as follows,

$Z_L=j{\omega }_{n}L$

Substitute $100\text{m}$ for L in the above equation as follows.

$\begin{array}{c}{Z}_L=jn\pi \left(100\times {10}^{-3}\right)\left\{\because {\omega }_n=n{\omega }_0=n\pi ,1\text{m}={10}^{-3}\right\}\\ =j0.1n\pi \end{array}$

The impedance of the capacitor is calculated as follows,

$Z_C=\frac{1}{j{\omega }_{n}C}$

Substitute $50\text{m}$ for C in the above equation as follows.

$\begin{array}{c}{Z}_C=\frac{1}{jn\pi \left(50\times {10}^{-3}\right)}\left\{\because {\omega }_n=n{\omega }_0=n\pi ,1\text{m}={10}^{-3}\right\}\\ =\frac{-j}{n\pi \left(0.05\right)}\\ =\frac{-j20}{n\pi }\end{array}$

The modified circuit is shown in Figure 1.

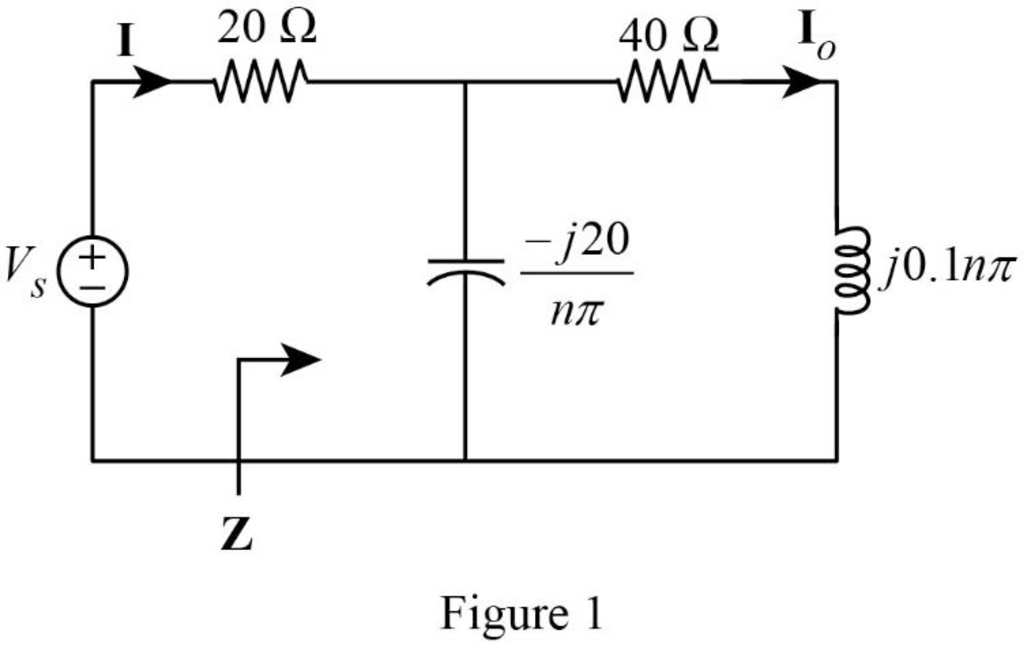
In Figure 1, the impedance is,

$\begin{array}{c}Z=\left(\frac{-j20}{n\pi }\right)\left|\right|\left(40+j0.1n\pi \right)\\ =\frac{\left(\frac{-j20}{n\pi }\right)\left(40+j0.1n\pi \right)}{\left(\frac{-j20}{n\pi }\right)+\left(40+j0.1n\pi \right)}\\ =\frac{\left(\frac{-j20}{n\pi }\right)\left(40+j0.1n\pi \right)}{\frac{-j20+\left(40n\pi +j0.1n^2{\pi }^2\right)}{n\pi }}\\ =\frac{\left(-j20\right)\left(40+j0.1n\pi \right)}{-j20+\left(40n\pi +j0.1n^2{\pi }^2\right)}\end{array}$

Simplify the above equation as follows,

$Z=\frac{2n\pi -j800}{40n\pi +j\left(0.1n^2{\pi }^2-20\right)}$

The impedance $Z_{in}$ is,

$Z_{in}=20+Z$

Substitute $\frac{2n\pi -j800}{40n\pi +j\left(0.1n^2{\pi }^2-20\right)}$ for $Z$ to find $Z_{in}$.

$\begin{array}{c}{Z}_{in}=20+\left(\frac{2n\pi -j800}{40n\pi +j\left(0.1n^2{\pi }^2-20\right)}\right)\\ =\frac{800n\pi +j\left(2n^2{\pi }^2-400\right)+2n\pi -j800}{40n\pi +j\left(0.1n^2{\pi }^2-20\right)}\\ =\frac{802n\pi +j\left(2n^2{\pi }^2-1200\right)}{40n\pi +j\left(0.1n^2{\pi }^2-20\right)}\end{array}$

The current $I$ through the 20 ohms resistor is,

$I=\frac{V_s}{Z_{in}}$

Substitute $\frac{20}{n\pi }$ for $V_s$ and $\frac{802n\pi +j\left(2n^2{\pi }^2-1200\right)}{40n\pi +j\left(0.1n^2{\pi }^2-20\right)}$ for $Z_{in}$ to find $I$.

$\begin{array}{c}I=\frac{\left(\frac{20}{n\pi }\right)}{\left(\frac{802n\pi +j\left(2n^2{\pi }^2-1200\right)}{40n\pi +j\left(0.1n^2{\pi }^2-20\right)}\right)}\\ =\frac{\left(\frac{20}{n\pi }\right)\left(40n\pi +j\left(0.1n^2{\pi }^2-20\right)\right)}{\left(802n\pi +j\left(2n^2{\pi }^2-1200\right)\right)}\\ =\frac{\left(800n\pi +j\left(2n^2{\pi }^2-400\right)\right)}{n\pi \left(802n\pi +j\left(2n^2{\pi }^2-1200\right)\right)}\\ =\frac{\left(800n\pi +j2\left(n^2{\pi }^2-200\right)\right)}{n\pi \left(802n\pi +j\left(2n^2{\pi }^2-1200\right)\right)}\end{array}$

The current $I_o$ through the inductor is,

$\begin{array}{c}{I}_o=\frac{\left(\frac{-j20}{n\pi }\right)I}{\frac{-j20}{n\pi }+\left(40+j0.1n\pi \right)}\\ =\frac{\left(\frac{-j20}{n\pi }\right)I}{\frac{-j20+\left(40n\pi +j0.1n^2{\pi }^2\right)}{n\pi }}\\ I_o=\frac{-j20I}{40n\pi +j\left(0.1n^2{\pi }^2-20\right)}\end{array}$

Substitute $\frac{\left(800n\pi +j2\left(n^2{\pi }^2-200\right)\right)}{n\pi \left(802n\pi +j\left(2n^2{\pi }^2-1200\right)\right)}$ for $I$ to find $I_o$.

$\begin{array}{c}{I}_o=\frac{-j20\left(\frac{\left(800n\pi +j2\left(n^2{\pi }^2-200\right)\right)}{n\pi \left(802n\pi +j\left(2n^2{\pi }^2-1200\right)\right)}\right)}{40n\pi +j\left(0.1n^2{\pi }^2-20\right)}\\ =-j20\left(\frac{\left(800n\pi +j\left(2n^2{\pi }^2-400\right)\right)}{n\pi \left(802n\pi +j\left(2n^2{\pi }^2-1200\right)\right)}\right)\left(\frac{1}{40n\pi +j\left(0.1n^2{\pi }^2-20\right)}\right)\\ =-j20\left(\frac{\left(800n\pi +j\left(2n^2{\pi }^2-400\right)\right)}{n\pi \left(802n\pi +j\left(2n^2{\pi }^2-1200\right)\right)}\right)\left(\frac{20}{800n\pi +j\left(2n^2{\pi }^2-400\right)}\right)\\ =\frac{\left(-j20\right)\left(20\right)}{n\pi \left(802n\pi +j\left(2n^2{\pi }^2-1200\right)\right)}\end{array}$

Simplify the equation as follows,

$I_o=\frac{\left(-j400\right)}{n\pi \left(802n\pi +j\left(2n^2{\pi }^2-1200\right)\right)}$

The magnitude and phase angle of the current $I_o$ is,

$I_o=\frac{400\angle -90°-{\tan }^{-1}\left[\frac{\left(2n^2{\pi }^2-1200\right)}{\left(802n\pi \right)}\right]}{n\pi \sqrt{{\left(802\right)}^2+{\left(2n^2{\pi }^2-1200\right)}^2}}$

In the time domain,

$i_o\left(t\right)=\left[\frac{1}{10}+\frac{400}{\pi }{\displaystyle \sum _{k=1}^{\infty }{I}_n\sin \left(n\pi t-{\varphi }_n\right)}\right]\text{A,}n=2k-1$

Where,

The phase angle ${\varphi }_n$ is,

${\varphi }_n=90°+{\tan }^{-1}\left[\frac{\left(2n^2{\pi }^2-1200\right)}{\left(802n\pi \right)}\right]$

And,

The current $I_n$ is,

$I_n=\frac{1}{n\sqrt{{\left(804n\pi \right)}^2+\left(2n^2{\pi }^2-1200\right)}}$

Conclusion:

Thus, the current through the inductor $i_o\left(t\right)$ is

$i_o\left(t\right)=\left[\frac{1}{10}+\frac{400}{\pi }{\displaystyle \sum _{k=1}^{\infty }{I}_n\sin \left(n\pi t-{\varphi }_n\right)}\right]\text{A,}n=2k-1$.