
Concept explainers
Each of the double pulleys shown has a mass moment of inertia of 15 lb·ft·s2 and is initially at rest. The outside radius is 18 in., and the inner radius is 9 in. Determine (a) the angular acceleration of each pulley, (b) the angular velocity of each pulley after point A on the cord has moved 10 ft.
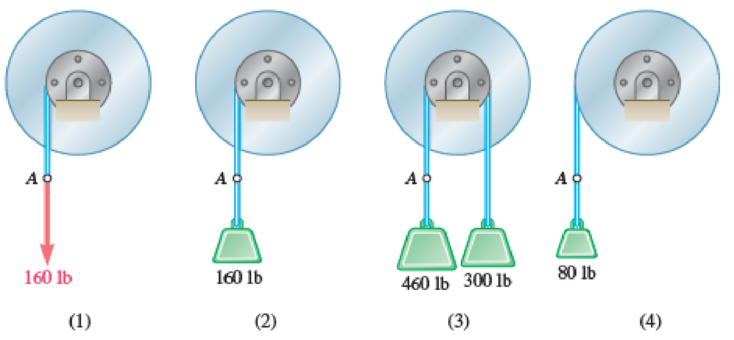
Fig. P16.34
(a)
Find the angular acceleration of the pulley 1
Find the angular acceleration of the pulley 2
Find the angular acceleration of the pulley 3
Find the angular acceleration of the pulley 4
Answer to Problem 16.34P
The angular acceleration of the pulley 1
The angular acceleration of the pulley 2
The angular acceleration of the pulley 3
The angular acceleration of the pulley 4
Explanation of Solution
The mass moment of inertia of the double pulleys
The outside radius of the pulley
The inner radius of the pulley
The finial angular velocity of the pulley
The load of the pulley 1
The load of the pulley 2
The left side load of the pulley 3
The right side load of the pulley 3
The load of the pulley 4
Calculation:
Consider the acceleration due to gravity (g) is
Case 1:
Convert the unit of the outside radius
Convert the unit of the inner radius
Show the free body diagram of the double pulley 1 as in Figure 1.

Here,
Refer to Figure 1.
Calculate the angular acceleration of the pulley 1
Calculate the moment about point O by applying the equation of equilibrium:
Hence, the angular acceleration of the pulley 1
Case 2:
Calculate the mass of the pulley 2
Substitute
Show the free body diagram of the double pulley 2 as in Figure 2.
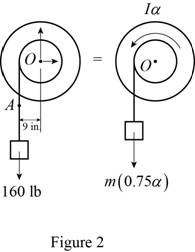
Refer to Figure 2.
Calculate the moment about point O by applying the equation of equilibrium:
Calculate the angular acceleration of the pulley 2
Substitute
Hence, the angular acceleration of the pulley 2
Case 3:
Calculate the left side mass of the pulley 3
Substitute
Calculate the right side mass of the pulley 3
Substitute
Show the free body diagram of the double pulley 3 as in Figure 3.
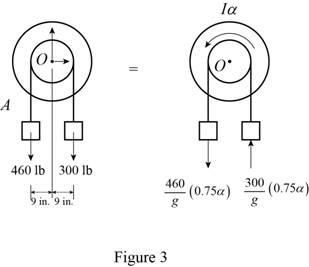
Refer to Figure 3.
Calculate the moment about point O by applying the equation of equilibrium:
Calculate the angular acceleration of the pulley 3
Substitute
Hence, the angular acceleration of the pulley 3
Case 4:
Calculate the left side mass of the pulley 4
Substitute
Show the free body diagram of the double pulley 4 as in Figure 4.
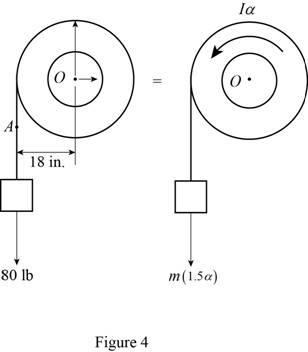
Refer to Figure 4.
Calculate the moment about point O by applying the equation of equilibrium:
Calculate the angular acceleration of the pulley 4
Substitute
Hence, the angular acceleration of the pulley 4
(b)
Find the angular velocity of the pulley 1
Find the angular velocity of the pulley 2
Find the angular velocity of the pulley 3
Find the angular velocity of the pulley 4
Answer to Problem 16.34P
The angular velocity of the pulley 1
The angular velocity of the pulley 2
The angular velocity of the pulley 3
The angular velocity of the pulley 4
Explanation of Solution
The mass moment of inertia of the double pulleys
The outside radius of the pulley
The inner radius of the pulley
The finial angular velocity of the pulley
The load of the pulley 1
The load of the pulley 2
The left side load of the pulley 3
The right side load of the pulley 3
The load of the pulley 4
The moved distance of the point A (l) is
Calculation:
Refer part (a).
Case 1:
Calculate the angle of the pulley 1
Substitute
Calculate the angular velocity of the pulley 1
Substitute
Hence, the angular velocity of the pulley 1
Case 2:
Calculate the angle of the pulley 2
Substitute
Calculate the angular velocity of the pulley 2
Substitute
Hence, the angular velocity of the pulley 2
Case 3:
Calculate the angle of the pulley 3
Substitute
Calculate the angular velocity of the pulley 3
Substitute
Hence, the angular velocity of the pulley 3
Case 4:
Calculate the angle of the pulley 4
Substitute
Calculate the angular velocity of the pulley 4
Substitute
Hence, the angular velocity of the pulley 4
Want to see more full solutions like this?
Chapter 16 Solutions
Connect 1 Semester Access Card for Vector Mechanics for Engineers: Statics and Dynamics
Additional Engineering Textbook Solutions
Management Information Systems: Managing The Digital Firm (16th Edition)
Database Concepts (8th Edition)
Starting Out with Java: From Control Structures through Objects (7th Edition) (What's New in Computer Science)
Elementary Surveying: An Introduction To Geomatics (15th Edition)
Electric Circuits. (11th Edition)
Fluid Mechanics: Fundamentals and Applications
- يكا - put 96** I need a detailed drawing with explanation or in wake, and the top edge of im below the free surface of the water. Determine the hydrothed if hydrostatic on the Plot the displacement diagram for a cam with roller follower of diameter 10 mm. The required motion is as follows; 1- Rising 60 mm in 135° with uniform acceleration and retardation motion. 2- Dwell 90° 3- Falling 60 mm for 135° with Uniform acceleration-retardation motion. Then design the cam profile to give the above displacement diagram if the minimum circle diameter of the cam is 50 mm. =--20125 7357 750 X 2.01arrow_forwardYou are working as an engineer in a bearing systems design company. The flow of lubricant inside a hydrodynamic bearing (µ = 0.001 kg m¯¹ s¯¹) can be approximated as a parallel, steady, two-dimensional, incompressible flow between two parallel plates. The top plate, representing the moving part of the bearing, travels at a constant speed, U, while the bottom plate remains stationary (Figure Q1). The plates are separated by a distance of 2h = 1 cm and are W = 20 cm wide. Their length is L = 10 cm. By applying the above approximations to the Navier-Stokes equations and assuming that end effects can be neglected, the horizontal velocity profile can be shown to be U y = +h У 2h = 1 cm 1 x1 y=-h u(y) = 1 dP 2μ dx -y² + Ay + B moving plate - U stationary plate 2 I2 L = 10 cm Figure Q1: Flow in a hydrodynamic bearing. The plates extend a width, W = 20 cm, into the page. (a) By considering the appropriate boundary conditions, show that the constants take the following forms: A = U 2h U 1 dP…arrow_forwardQuestion 2 You are an engineer working in the propulsion team for a supersonic civil transport aircraft driven by a turbojet engine, where you have oversight of the design for the engine intake and the exhaust nozzle, indicated in Figure Q2a. The turbojet engine can operate when provided with air flow in the Mach number range, 0.60 to 0.80. You are asked to analyse a condition where the aircraft is flying at 472 m/s at an altitude of 14,000 m. For all parts of the question, you can assume that the flow path of air through the engine has a circular cross section. (a) normal shock 472 m/s A B (b) intake engine altitude: 14,000 m D exhaust nozzle→ exit to atmosphere 472 m/s 50 m/s B diameter: DE = 0.30 m EX diameter: DF = 0.66 m Figure Q2: Propulsion system for a supersonic aircraft. F a) When the aircraft is at an altitude of 14,000 m, use the International Standard Atmosphere in the Module Data Book to state the local air pressure and tempera- ture. Thus show that the aircraft speed of…arrow_forward
- given below: A rectangular wing with wing twist yields the spanwise circulation distribution kbV1 roy) = kbv. (2) where k is a constant, b is the span length and V. is the free-stream velocity. The wing has an aspect ratio of 4. For all wing sections, the lift curve slope (ag) is 2 and the zero-lift angle of attack (a=0) is 0. a. Derive expressions for the downwash (w) and induced angle of attack a distributions along the span. b. Derive an expression for the induced drag coefficient. c. Calculate the span efficiency factor. d. Calculate the value of k if the wing has a washout and the difference between the geometric angles of attack of the root (y = 0) and the tip (y = tb/2) is: a(y = 0) a(y = ±b/2) = /18 Hint: Use the coordinate transformation y = cos (0)arrow_forward۳/۱ العنوان O не شكا +91x PU + 96852 A heavy car plunges into a lake during an accident and lands at the bottom of the lake on its wheels as shown in figure. The door is 1.2 m high and I m wide, and the top edge of Deine the hadrostatic force on the Plot the displacement diagram for a cam with roller follower of diameter 10 mm. The required motion is as follows; 1- Rising 60 mm in 135° with uniform acceleration and retardation motion. 2- Dwell 90° 3- Falling 60 mm for 135° with Uniform acceleration-retardation motion. Then design the cam profile to give the above displacement diagram if the minimum circle diameter of the cam is 50 mm. = -20125 750 x2.01arrow_forwardPlot the displacement diagram for a cam with roller follower of diameter 10 mm. The required motion is as follows; 1- Rising 60 mm in 135° with uniform acceleration and retardation motion. 2- Dwell 90° 3- Falling 60 mm for 135° with Uniform acceleration-retardation motion. Then design the cam profile to give the above displacement diagram if the minimum circle diameter of the cam is 50 mm.arrow_forward
- Q1/ A vertical, circular gate with water on one side as shown. Determine the total resultant force acting on the gate and the location of the center of pressure, use water specific weight 9.81 kN/m³ 1 m 4 marrow_forwardI need handwritten solution with sketches for eacharrow_forwardGiven answers to be: i) 14.65 kN; 6.16 kN; 8.46 kN ii) 8.63 kN; 9.88 kN iii) Bearing 6315 for B1 & B2, or Bearing 6215 for B1arrow_forward
- (b) A steel 'hot rolled structural hollow section' column of length 5.75 m, has the cross-section shown in Figure Q.5(b) and supports a load of 750 kN. During service, it is subjected to axial compression loading where one end of the column is effectively restrained in position and direction (fixed) and the other is effectively held in position but not in direction (pinned). i) Given that the steel has a design strength of 275 MN/m², determine the load factor for the structural member based upon the BS5950 design approach using Datasheet Q.5(b). [11] ii) Determine the axial load that can be supported by the column using the Rankine-Gordon formula, given that the yield strength of the material is 280 MN/m² and the constant *a* is 1/30000. [6] 300 600 2-300 mm wide x 5 mm thick plates. Figure Q.5(b) L=5.75m Pinned Fixedarrow_forwardHelp ارجو مساعدتي في حل هذا السؤالarrow_forwardHelp ارجو مساعدتي في حل هذا السؤالarrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





