
Recent interest in competitive and recreational cycling has meant that engineers have directed their skills toward the designand testing of mountain bikes (Fig. P16.33a). Suppose that you are given the task of predicting the horizontal and vertical displacement of a bike bracketing system in response to a force. Assume the forces you must analyze can be simplified as depicted in Fig. P16.33b. You are interested in testing the response of the truss to a force exerted in any number of directions designated by the angle
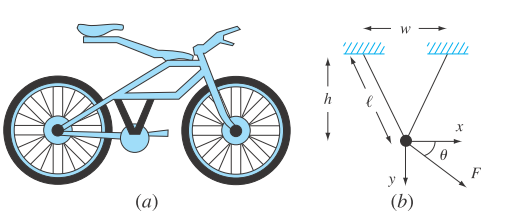
FIGURE P16.33
(a) A mountain bike along with (b) a free-body diagram for a part of the frame.
To calculate: The minimum potential energy with displacement
Answer to Problem 33P
Solution:
The minimum potential energy with displacement
Explanation of Solution
Given Information:
The parameters are given as Young’s modulus E is

Calculation:
Consider the free body diagram,

The potential energy at a position where horizontal displacement is x and vertical displacement is y, first consider the angular deflection of the bracket and then use the concept of energy stored in a bracket system due to deflection.
For
Substitute the values
To minimize this, the excel solver can be used to solve for the displacement.
The excel solver steps are,
Step 1. Initiate quantity
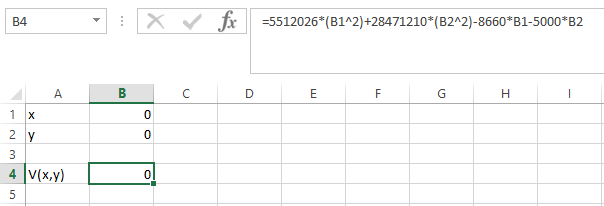
Step 2. Apply the formula in
Step 3. Go to DATA and then click on Solver. This dialog box will appear.
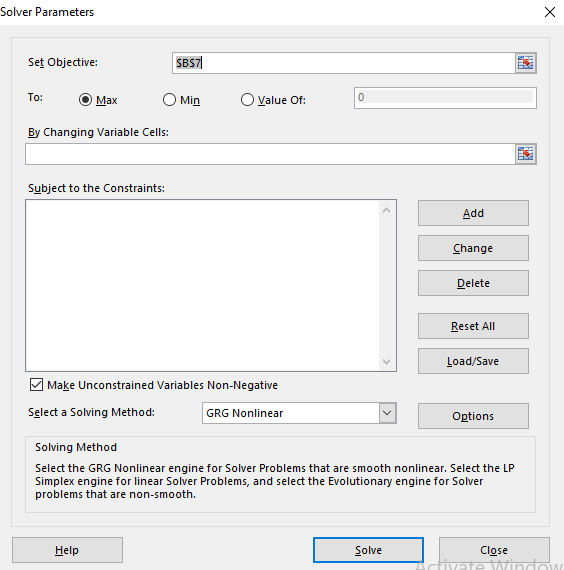
Step 4. Select the set objective, min, changing variable then this dialog box appears.

Step 5. Click on Solve and then OK.
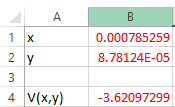
Hence, the minimum potential energy with displacement
Put
The potential energy can be found out with upper procedure as
The potential energy will be
Thus from the above analysis, it can be concluded that x deflection is maximum when load is pointed in the x direction and y deflection is maximum when load is pointed in the y direction.
However x deflection is more than y direction as potential energy is higher at lower angle.
This can also be concluded that if w values increases then deflection would be more uniform throughout.
Want to see more full solutions like this?
Chapter 16 Solutions
Numerical Methods for Engineers
- Use the Euclidean algorithm to find two sets of integers (a, b, c) such that 55a65b+143c: Solution = 1. By the Euclidean algorithm, we have: 143 = 2.65 + 13 and 65 = 5.13, so 13 = 143 – 2.65. - Also, 55 = 4.13+3, 13 = 4.3 + 1 and 3 = 3.1, so 1 = 13 — 4.3 = 13 — 4(55 – 4.13) = 17.13 – 4.55. Combining these, we have: 1 = 17(143 – 2.65) - 4.55 = −4.55 - 34.65 + 17.143, so we can take a = − −4, b = −34, c = 17. By carrying out the division algorithm in other ways, we obtain different solutions, such as 19.55 23.65 +7.143, so a = = 9, b -23, c = 7. = = how ? come [Note that 13.55 + 11.65 - 10.143 0, so we can obtain new solutions by adding multiples of this equation, or similar equations.]arrow_forward- Let n = 7, let p = 23 and let S be the set of least positive residues mod p of the first (p − 1)/2 multiple of n, i.e. n mod p, 2n mod p, ..., p-1 2 -n mod p. Let T be the subset of S consisting of those residues which exceed p/2. Find the set T, and hence compute the Legendre symbol (7|23). 23 32 how come? The first 11 multiples of 7 reduced mod 23 are 7, 14, 21, 5, 12, 19, 3, 10, 17, 1, 8. The set T is the subset of these residues exceeding So T = {12, 14, 17, 19, 21}. By Gauss' lemma (Apostol Theorem 9.6), (7|23) = (−1)|T| = (−1)5 = −1.arrow_forwardLet n = 7, let p = 23 and let S be the set of least positive residues mod p of the first (p-1)/2 multiple of n, i.e. n mod p, 2n mod p, ..., 2 p-1 -n mod p. Let T be the subset of S consisting of those residues which exceed p/2. Find the set T, and hence compute the Legendre symbol (7|23). The first 11 multiples of 7 reduced mod 23 are 7, 14, 21, 5, 12, 19, 3, 10, 17, 1, 8. 23 The set T is the subset of these residues exceeding 2° So T = {12, 14, 17, 19, 21}. By Gauss' lemma (Apostol Theorem 9.6), (7|23) = (−1)|T| = (−1)5 = −1. how come?arrow_forward
- Shading a Venn diagram with 3 sets: Unions, intersections, and... The Venn diagram shows sets A, B, C, and the universal set U. Shade (CUA)' n B on the Venn diagram. U Explanation Check A- B Q Search 田arrow_forwardWhat is the area of this figure? 5 mm 4 mm 3 mm square millimeters 11 mm Submit 8 mm Work it out 9 mmarrow_forwardPlease explain how come of X2(n).arrow_forward
- No chatgpt pls will upvotearrow_forwardFind all solutions of the polynomial congruence x²+4x+1 = 0 (mod 143). (The solutions of the congruence x² + 4x+1=0 (mod 11) are x = 3,4 (mod 11) and the solutions of the congruence x² +4x+1 = 0 (mod 13) are x = 2,7 (mod 13).)arrow_forwardDetermine whether each function is an injection and determine whether each is a surjection.The notation Z_(n) refers to the set {0,1,2,...,n-1}. For example, Z_(4)={0,1,2,3}. f: Z_(6) -> Z_(6) defined by f(x)=x^(2)+4(mod6). g: Z_(5) -> Z_(5) defined by g(x)=x^(2)-11(mod5). h: Z*Z -> Z defined by h(x,y)=x+2y. j: R-{3} -> R defined by j(x)=(4x)/(x-3).arrow_forward
- Determine whether each function is an injection and determine whether each is a surjection.arrow_forwardLet A = {a, b, c, d}, B = {a,b,c}, and C = {s, t, u,v}. Draw an arrow diagram of a function for each of the following descriptions. If no such function exists, briefly explain why. (a) A function f : AC whose range is the set C. (b) A function g: BC whose range is the set C. (c) A function g: BC that is injective. (d) A function j : A → C that is not bijective.arrow_forwardLet f:R->R be defined by f(x)=x^(3)+5.(a) Determine if f is injective. why?(b) Determine if f is surjective. why?(c) Based upon (a) and (b), is f bijective? why?arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage


