
Concept explainers
The flow
where
(a) Given the parameters n
(b) Repeat part (a), but include the cost of excavation. To do this minimize the following cost function,
where
(c) Discuss the implications of your results.
(a)
To calculate: The values of that will minimize the wetted perimeter P if the Manning equation of flow Q
can be written as
Answer to Problem 19P
Solution:
The values of
that will minimize the wetted perimeter P is
respectively.
Explanation of Solution
Given Information:
The Manning equation of flow Q
can be written as
where n is Manning roughness coefficient,
is cross-sectional are of channel
is given by
where P is wetted perimeter and it is defined by
where H is depth
and the parameters value are given as
Calculation:
Consider the equation,
The constrained can be written as,
This problem can be solved out by Linear programming formulation.
To minimize the wetted perimeter P function with the given constraint, the excel solver can be used.
The excel solver steps are,
Step 1. Initiate quantity
and then write the parameter as shown below,

Step 2. Apply the formula in
as shown below,
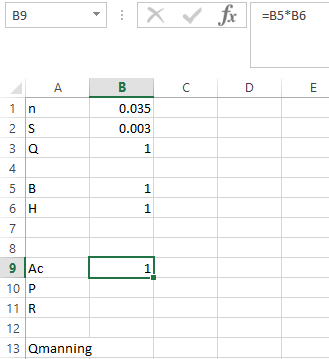
Step 3. Apply the formula in P as shown below,
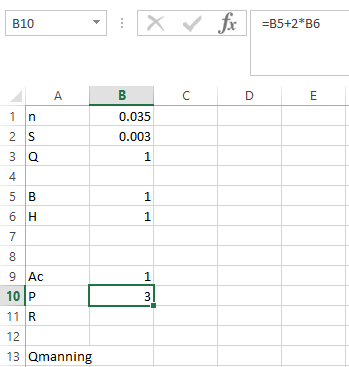
Step 4. Apply the formula in R as shown below,

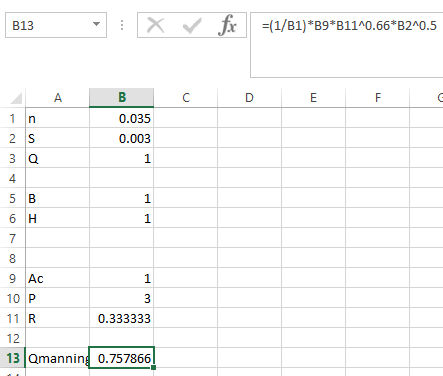
Step 5. Apply the formula in Qmanning as shown below,
Step 6. Go to DATA and then click on Solver. This dialog box will appear.
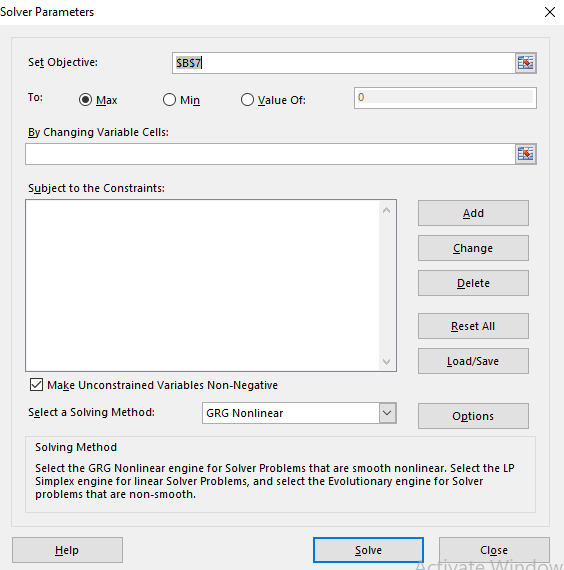
Step 7. Select the set objective, min, changing variable and then add,
Step 8. Click OK then this dialog box appears.
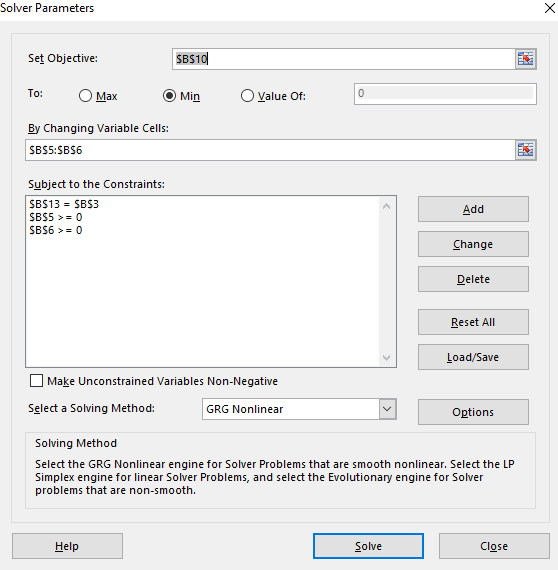
Step 9. Click on Solve and then OK.
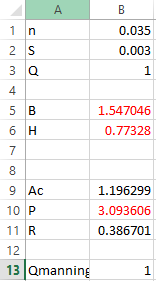
Hence, the values of
that will minimize the wetted perimeter P is
respectively.
(b)
To calculate: The values of
that will minimize the excavation cost function
is
and cost factor for lining
if the Manning equation of flow Q
can be written as
Answer to Problem 19P
Solution:
The values of
that will minimize the cost function P is
respectively.
Explanation of Solution
Given Information:
The Manning equation of flow Q
can be written as
where n is Manning roughness coefficient,
is cross-sectional are of channel
is given by
where P is wetted perimeter and it is defined by
where H is depth
and the parameters value are given as
Calculation:
Consider the function,
The constrained can be written as,
This problem can be solved out by Linear programming formulation.
To minimize the cost function with the given constraint, the excel solver can be used.
The excel solver steps are,
Step 1. Initiate quantity
and then write the parameter as shown below,

Step 2. Apply the formula in
as shown below,

Step 3. Apply the formula in P as shown below,

Step 4. Apply the formula in R as shown below,

Step 5. Apply the formula in Qmanning as shown below,

Step 6. Apply the formula in Cost as shown below,
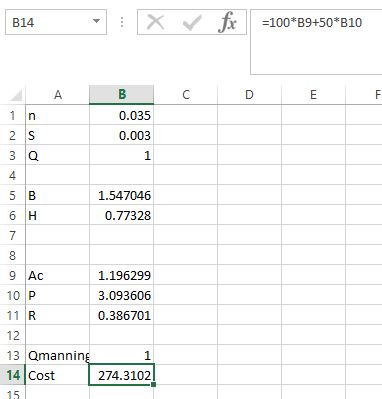
Step 7. Go to DATA and then click on Solver. This dialog box will appear.

Step 8. Select the set objective, min, changing variable and then add,

Step 9. Click OK then this dialog box appears.

Step 10. Click on Solve and then OK.
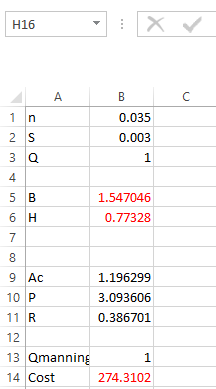
Hence, the values of
that will minimize the cost function is
respectively.
(c)
The implication of the result obtained in part (a) and part (b).
Answer to Problem 19P
Solution:
This can be interpreted that both the excavation and limiting cost can be minimized simultaneously by considering the bottom width B that is twice the length of each vertical side H.
Explanation of Solution
To interpret the result, first consider the constraint equation,
And,
On further simplification,
As
are dependent on B and H, thus both have minimized.
Thus, the excavation cost function
is minimized and as excavation cost C is directly proportional to cross-sectional area.
Hence, both the excavation and limiting cost can be minimized simultaneously by considering the bottom width B that is twice the length of each vertical side H as obtained in part (a) and (b) as
Want to see more full solutions like this?
Chapter 16 Solutions
Numerical Methods for Engineers
- My ID# 016948724 please solve the proble step by step find the forces fx=o: fy=0; fz=0; and find shear moment and the bending moment diagran please draw the diagram for the shear and bending momentarrow_forwardMy ID#016948724. Please help me to find the moment of inertia lx ly are a please show to solve step by stepsarrow_forwardplease solve this problem step by steparrow_forward
- Please do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forward
- [Q2]: The cost information supplied by the cost accountant is as follows:Sales 20,00 units, $ 10 per unitCalculate the (a/ newsale guantity and (b) new selling price to earn the sameVariable cost $ 6 per unit, Fixed Cost $ 30,000, Profit $ 50,000profit ifi) Variable cost increases by $ 2 per unitil) Fixed cost increase by $ 10,000Ili) Variable cost increase by $ 1 per unit and fixed cost reduces by $ 10,000arrow_forwardcan you please help me perform Visual Inspection and Fractography of the attatched image: Preliminary examination to identify the fracture origin, suspected fatigue striation, and corrosion evidences.arrow_forwardcan you please help[ me conduct Causal Analysis (FTA) on the scenario attatched: FTA diagram which is a fault tree analysis diagram will be used to gain an overview of the entire path of failure from root cause to the top event (i.e., the swing’s detachment) and to identify interactions between misuse, material decay and inspection errors.arrow_forward
 Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L Refrigeration and Air Conditioning Technology (Mi...Mechanical EngineeringISBN:9781305578296Author:John Tomczyk, Eugene Silberstein, Bill Whitman, Bill JohnsonPublisher:Cengage Learning
Refrigeration and Air Conditioning Technology (Mi...Mechanical EngineeringISBN:9781305578296Author:John Tomczyk, Eugene Silberstein, Bill Whitman, Bill JohnsonPublisher:Cengage Learning Automotive Technology: A Systems Approach (MindTa...Mechanical EngineeringISBN:9781133612315Author:Jack Erjavec, Rob ThompsonPublisher:Cengage Learning
Automotive Technology: A Systems Approach (MindTa...Mechanical EngineeringISBN:9781133612315Author:Jack Erjavec, Rob ThompsonPublisher:Cengage Learning Precision Machining Technology (MindTap Course Li...Mechanical EngineeringISBN:9781285444543Author:Peter J. Hoffman, Eric S. Hopewell, Brian JanesPublisher:Cengage Learning
Precision Machining Technology (MindTap Course Li...Mechanical EngineeringISBN:9781285444543Author:Peter J. Hoffman, Eric S. Hopewell, Brian JanesPublisher:Cengage Learning Electrical Transformers and Rotating MachinesMechanical EngineeringISBN:9781305494817Author:Stephen L. HermanPublisher:Cengage Learning
Electrical Transformers and Rotating MachinesMechanical EngineeringISBN:9781305494817Author:Stephen L. HermanPublisher:Cengage Learning





