Chapter 15, Problem 15.5P

(a)

Interpretation Introduction

Interpretation:

To graph the figures for $A=\frac{975}{T}-18.4+3\ln T$

Concept Introduction:

Plot A v/s T by varying T and finding respective values of A

  $A=\frac{975}{T}-18.4+3\ln T$

Plot T v/s x,by varying T, find respective values of x using the below equation,

  $A(1-2x)=\ln \left(\frac{1-x}{x}\right)$

Where,

T = TemperaturE

x = Mole fraction

UCST = Upper Critical Solution TemperaturE

LCST = Lower Critical Solution TemperaturE

Answer to Problem 15.5P

The corresponding figures of A v/s T and T v/s x are plotted.

Explanation of Solution

  $A=\frac{975}{T}-18.4+3\ln T$

Using the above equation and varying T,

Now, Plot A v/s T, we get,

T	A	T	A	T	A	T	A
250	2.064383	305	1.957657	355	1.962832	405	2.019069
255	2.04732	310	1.954878	360	1.966645	410	2.02652
260	2.032045	315	1.952956	365	1.970925	415	2.034233
265	2.018435	320	1.951838	370	1.975644	420	2.042193
270	2.006377	325	1.951476	375	1.980778	425	2.050385
275	1.995768	330	1.951823	380	1.986303	430	2.058797
280	1.986512	335	1.952839	385	1.992198	435	2.067417
285	1.97852	340	1.954484	390	1.99844	440	2.076233
290	1.971712	345	1.95672	395	2.005012	445	2.085234
295	1.966011	350	1.959514	400	2.011894	450	2.094409
300	1.961347					455	2.103749

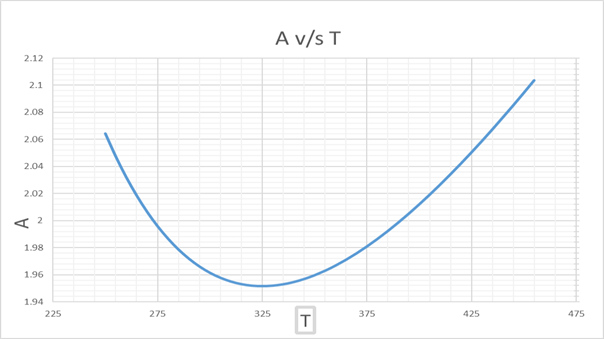
From this graph of A v/s T, we get,

A =2 at T = 272.92 K and 391.209 K

Hence, we get that, UCST = 272.92 K

and

LCST = 391.2 K

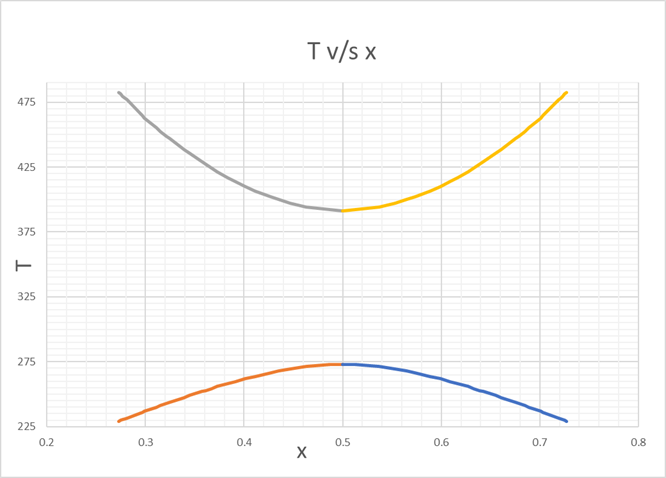
Since, There are 2 points for A =2, We can plot T v/s x

Varying T from

225 K to UCST

And from

LCST to 482 K

For finding x,

  $A(1-2x)=\ln \left(\frac{1-x}{x}\right)$

  $A=\frac{1}{(1-2x)}\ln \left(\frac{1-x}{x}\right)$

  $A=\frac{975}{T}-18.4+3\ln T$

Varying, T, we find the values of x respectively upto 3 decimals.

We can see that the values of T are same for x and (1-x).

We find the corresponding values, for T v/s x, as below,

x	A	x	A	A	T
0.273	2.157389	0.727	2.157389	2.157711656	229.2
0.275	2.154223	0.725	2.154223	2.15444794	229.8
0.277	2.151103	0.723	2.151103	2.15122162	230.4
0.279	2.148026	0.721	2.148026	2.148032352	231
0.281	2.144992	0.719	2.144992	2.144879797	231.6
0.295	2.124933	0.705	2.124933	2.125260129	235.5
0.297	2.122228	0.703	2.122228	2.122372431	236.1
0.299	2.119563	0.701	2.119563	2.119518699	236.7
0.311	2.104361	0.689	2.104361	2.10441677	240
0.315	2.099584	0.685	2.099584	2.099167952	241.2
0.321	2.092682	0.679	2.092682	2.092783653	242.7
0.325	2.08825	0.675	2.08825	2.089045662	243.6
0.339	2.073769	0.661	2.073769	2.073625685	247.5
0.345	2.068035	0.655	2.068035	2.06802134	249
0.357	2.057374	0.643	2.057374	2.057334882	252
0.361	2.054052	0.639	2.054052	2.054261227	252.9
0.367	2.04928	0.633	2.04928	2.049270664	254.4
0.373	2.044756	0.627	2.044756	2.044442293	255.9
0.383	2.037752	0.617	2.037752	2.037948522	258
0.391	2.032618	0.609	2.032618	2.032623149	259.8
0.401	2.026769	0.599	2.026769	2.026683214	261.9
0.411	2.021534	0.589	2.021534	2.02181967	263.7
0.427	2.014395	0.573	2.014395	2.014166319	266.7
0.435	2.011382	0.565	2.011382	2.011259023	267.9
0.447	2.007542	0.553	2.007542	2.007745467	269.4
0.463	2.003663	0.537	2.003663	2.003702412	271.2
0.487	2.000451	0.513	2.000451	2.000474405	272.7

x	A	x	A	A	T
0.273	2.157389	0.727	2.157389	2.1576682	482.5
0.275	2.154223	0.725	2.154223	2.1556408	481.5
0.277	2.151103	0.723	2.151103	2.1515998	479.5
0.279	2.148026	0.721	2.148026	2.1483803	477.9
0.281	2.144992	0.719	2.144992	2.1465746	477
0.295	2.124933	0.705	2.124933	2.1248316	466
0.297	2.122228	0.703	2.122228	2.1221099	464.6
0.299	2.119563	0.701	2.119563	2.1190127	463
0.311	2.104361	0.689	2.104361	2.1046921	455.5
0.315	2.099584	0.685	2.099584	2.0990594	452.5
0.321	2.092682	0.679	2.092682	2.0925609	449
0.325	2.08825	0.675	2.08825	2.0888838	447
0.339	2.073769	0.661	2.073769	2.0735686	438.5
0.345	2.068035	0.655	2.068035	2.0682904	435.5
0.357	2.057374	0.643	2.057374	2.057098	429
0.361	2.054052	0.639	2.054052	2.0545646	427.5
0.367	2.04928	0.633	2.04928	2.0495558	424.5
0.373	2.044756	0.627	2.044756	2.0446266	421.5
0.383	2.037752	0.617	2.037752	2.0373882	417
0.391	2.032618	0.609	2.032618	2.0326704	414
0.401	2.026769	0.599	2.026769	2.0265203	410
0.411	2.021534	0.589	2.021534	2.0212758	406.5
0.427	2.014395	0.573	2.014395	2.0147294	402
0.435	2.011382	0.565	2.011382	2.0118936	400
0.447	2.007542	0.553	2.007542	2.0077282	397
0.463	2.003663	0.537	2.003663	2.003672	394
0.5	2	0.5	2	2	391.2092

(b)

Interpretation Introduction

Interpretation:

To graph the figures for $A=\frac{540}{T}-17.1+3\ln T$

Concept Introduction:

Plot A v/s T by varying T and finding respective values of A

  $A=\frac{540}{T}-17.1+3\ln T$

Plot T v/s x, by varying T, find respective values of x using the below equation,

  $A(1-2x)=\ln \left(\frac{1-x}{x}\right)$

Where,

T = TemperaturE

x = Mole fraction

UCST = Upper Critical Solution TemperaturE

LCST = Lower Critical Solution TemperaturE

Answer to Problem 15.5P

The corresponding figures of A v/s T and T v/s x are plotted.

Explanation of Solution

  $A=\frac{540}{T}-17.1+3\ln T$

Using the above equation and varying T,

Now, Plot A v/s T, we get,

T	A	T	A	T	A	T	A
250	1.624382754	305	1.831427133	355	2.037480129	405	2.244994535
255	1.641437694	310	1.851652376	360	2.058312094	410	2.26554465
260	1.65896797	315	1.872003631	365	2.079144116	415	2.28604038
265	1.676925327	320	1.892462987	370	2.099968476	420	2.30647842
270	1.695265877	325	1.913014009	375	2.120778078	425	2.326855742
275	1.713949657	330	1.9336416	380	2.14156639	430	2.34716958
280	1.732940238	335	1.954331894	385	2.162327405	435	2.367417404
285	1.752204383	340	1.975072147	390	2.183055602	440	2.387596908
290	1.771711734	345	1.995850642	395	2.203745902	445	2.407705993
295	1.791434544	350	2.016656606	400	2.224393641	450	2.427742748
300	1.811347424					455	2.447705444

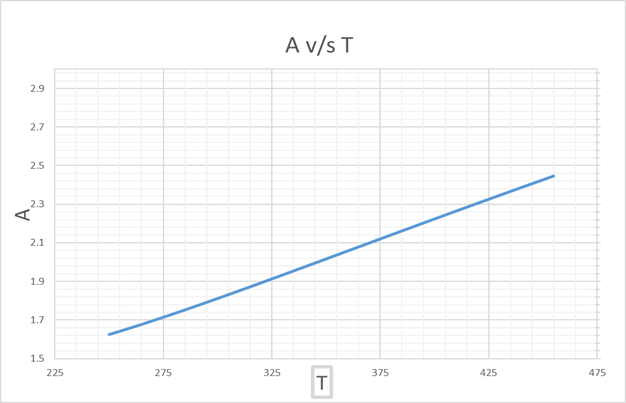
From this graph of A v/s T, we get,

A =2 at T = 346 K

Hence, we get that,

LCST = 391.2 K

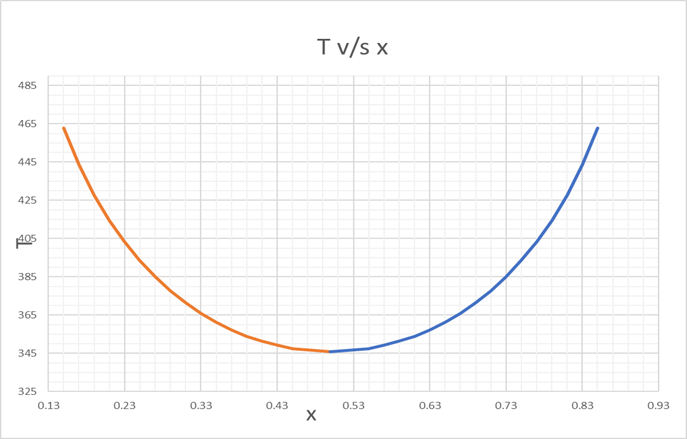
Since, there is only 1 point for A =2, we can plot T v/s x

And from

LCST to 482 K

For finding x,

  $A(1-2x)=\ln \left(\frac{1-x}{x}\right)$

  $A=\frac{1}{(1-2x)}\ln \left(\frac{1-x}{x}\right)$

  $A=\frac{540}{T}-17.1+3\ln T$

Varying, T, we find the values of x respectively upto 3 decimals.

We can see that the values of T are same for x and (1-x).

We find the corresponding values, for T v/s x, as below,

x	A	x	A	A	T
0.15	2.478002	0.85	2.478002	2.4783	462.7
0.17	2.402466	0.83	2.402466	2.402485	443.7
0.19	2.338726	0.81	2.338726	2.338239	427.8
0.21	2.284354	0.79	2.284354	2.284403	414.6
0.23	2.237613	0.77	2.237613	2.237938	403.286
0.25	2.197225	0.75	2.197225	2.197543	393.5
0.27	2.162223	0.73	2.162223	2.162327	385
0.29	2.131867	0.71	2.131867	2.131591	377.6
0.31	2.105577	0.69	2.105577	2.105381	371.3
0.33	2.082897	0.67	2.082897	2.082893	365.9
0.35	2.063464	0.65	2.063464	2.063729	361.3
0.37	2.046988	0.63	2.046988	2.046771	357.23
0.39	2.033237	0.61	2.033237	2.033314	354
0.41	2.02203	0.59	2.02203	2.022069	351.3
0.43	2.013223	0.57	2.013223	2.013326	349.2
0.45	2.006707	0.55	2.006707	2.006251	347.5
0.47	2.002405	0.53	2.002405	2.002922	346.7
0.49	2.000267	0.51	2.000267	2.000634	346.15
0.5	2	0.5	2	2.00001	346

(c)

Interpretation Introduction

Interpretation:

To graph the figures for $A=\frac{1500}{T}-19.9+3\ln T$

Concept Introduction:

Plot A v/s T by varying T and finding respective values of A

  $A=\frac{1500}{T}-19.9+3\ln T$

Plot T v/s x, by varying T, find respective values of x using the below equation,

  $A(1-2x)=\ln \left(\frac{1-x}{x}\right)$

Where,

T = TemperaturE

x = Mole fraction

UCST = Upper Critical Solution TemperaturE

LCST = Lower Critical Solution TemperaturE

Answer to Problem 15.5P

The corresponding figures of A v/s T and T v/s x are plotted.

Explanation of Solution

  $A=\frac{1500}{T}-19.9+3\ln T$

Using the above equation and varying T,

Now, Plot A v/s T, we get,

T	A	T	A	T	A	T	A
250	2.664382754	305	2.178968117	355	1.941705481	405	1.815364905
255	2.606143577	310	2.14842657	360	1.924978761	410	1.807008064
260	2.551275662	315	2.119622678	365	1.909281102	415	1.799293392
265	2.499566836	320	2.092462987	370	1.894563071	420	1.792192705
270	2.450821433	325	2.066860162	375	1.880778078	425	1.785679271
275	2.404858748	330	2.042732509	380	1.867882179	430	1.779727719
280	2.361511667	335	2.020003536	385	1.855833899	435	1.774313955
285	2.320625436	340	1.998601559	390	1.844594064	440	1.76941509
290	2.282056562	345	1.978459338	395	1.834125649	445	1.765009363
295	2.245671832	350	1.959513749	400	1.824393641	450	1.761076082
300	2.211347424					455	1.757595554

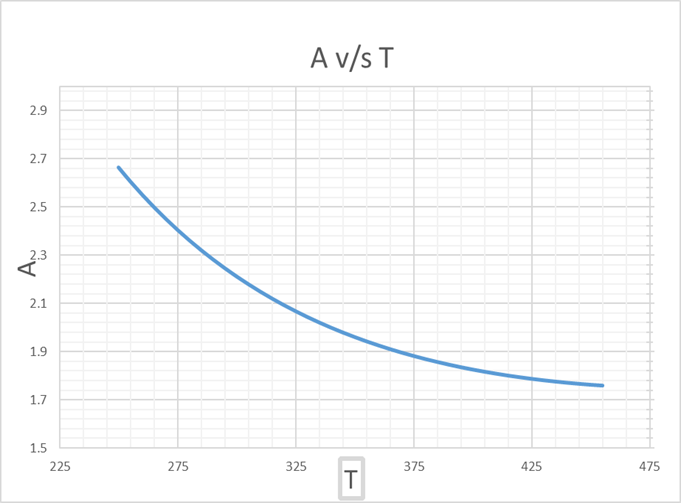
From this graph of A v/s T, we get,

A =2 at T = 339.66 K

Hence, we get that,

UCST = 339.66 K

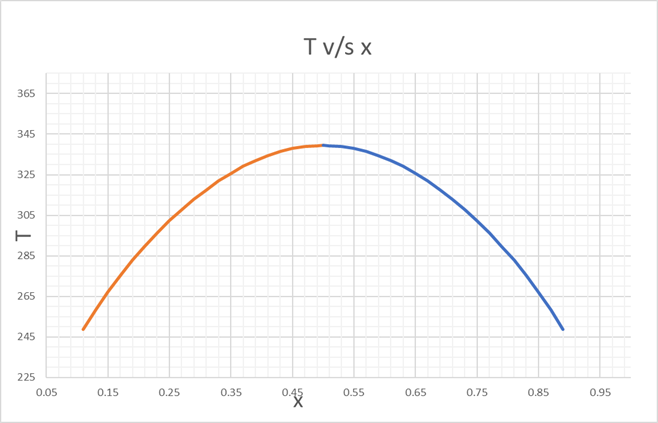
Since, there is only 1 point for A =2, we can plot T v/s x

And from

250 K to UCST

For finding x,

  $A(1-2x)=\ln \left(\frac{1-x}{x}\right)$

  $A=\frac{1}{(1-2x)}\ln \left(\frac{1-x}{x}\right)$

  $A=\frac{1500}{T}-19.9+3\ln T$

Varying, T, we find the values of x respectively up to 3 decimals.

We can see that the values of T are same for x and (1-x).

We find the corresponding values, for T v/s x, as below,

x	A	x	A	A	T
0.11	2.680437	0.89	2.680437	2.68011	248.7
0.13	2.568863	0.87	2.568863	2.56848	258.4
0.15	2.478002	0.85	2.478002	2.47874	267.1
0.17	2.402466	0.83	2.402466	2.40219	275.3
0.19	2.338726	0.81	2.338726	2.33801	282.838
0.21	2.284354	0.79	2.284354	2.28431	289.7
0.23	2.237613	0.77	2.237613	2.23725	296.2
0.25	2.197225	0.75	2.197225	2.19687	302.2
0.27	2.162223	0.73	2.162223	2.16225	307.7
0.29	2.131867	0.71	2.131867	2.13151	312.9
0.31	2.105577	0.69	2.105577	2.10552	317.56
0.33	2.082897	0.67	2.082897	2.08204	322
0.35	2.063464	0.65	2.063464	2.0634	325.7
0.37	2.046988	0.63	2.046988	2.0464	329.22
0.39	2.033237	0.61	2.033237	2.03348	332
0.41	2.02203	0.59	2.02203	2.02266	334.4
0.43	2.013223	0.57	2.013223	2.01345	336.5
0.45	2.006707	0.55	2.006707	2.00658	338.1
0.47	2.002405	0.53	2.002405	2.00278	339
0.49	2.000267	0.51	2.000267	2.00194	339.2
0.5	2	0.5		2	339.663