Chapter 1.4, Problem 63AYU

To determine

To explain: the position of the arm, the length andwhen to use more than one arm

Answer to Problem 63AYU

Square field:

It is concluded that the arm should be positioned at a distance of $\frac{s}{\sqrt{2}}$ units away from the corners and the length of the arm is $\frac{s}{\sqrt{2}}$ .

Rectangular field:

It is concluded that the arm should be positioned at a distance of $\frac{\sqrt{l^2+w^2}}{2}$ units away from the corners and the length of the arm is $\frac{\sqrt{l^2+w^2}}{2}$ .

A circle is not circumscribed around a long rectangle with the diagonal as its diameter. Thus, it becomes desirable to use more than one arm.

Explanation of Solution

Given:

  

First, consider the square field. Let s be the side length of the square field.

  

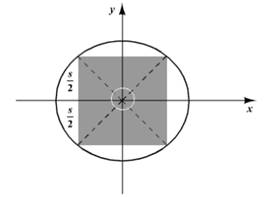
From the figure, the arm is positioned at the center of the circle and its length should be the radius.

By the Pythagorean theorem, the diagonal of the square field is $\sqrt{2}s$ . The center of the circle is at the intersection of the diagonals.

That is, the center of the circle is $\frac{s}{\sqrt{2}}$ units away from the corners. The radius of the circle is half the length of the diagonal, which is also $\frac{s}{\sqrt{2}}$ .

Thus, it is concluded that the arm should be positioned at a distance of $\frac{s}{\sqrt{2}}$ units away from the corners and the length of the arm is $\frac{s}{\sqrt{2}}$ .

Now, consider the rectangular field. Let $l$ be the length of the field and $w$ be the width.

  

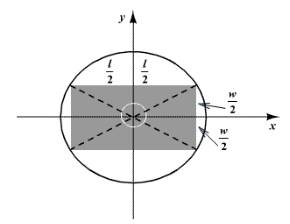
In this case also, the arm is positioned at the center of the circle and its length should be the radius.

By the Pythagorean theorem, the diagonal of the rectangular field is $\sqrt{l^2+w^2}$ . The center of the circle is at the intersection of the diagonals.

That is, the center of the circle is $\frac{\sqrt{l^2+w^2}}{2}$ units away from the corners. The radius of the circle is half the length of the diagonal, which is also $\frac{\sqrt{l^2+w^2}}{2}$ .

Thus, it is concluded that the arm should be positioned at a distance of $\frac{\sqrt{l^2+w^2}}{2}$ units away from the corners and the length of the arm is $\frac{\sqrt{l^2+w^2}}{2}$ .

When the length of a rectangular field is much larger than its width, the watering pattern cannot be a circle. This is because a circle is not circumscribed around a long rectangle with the diagonal as its diameter.

Thus, it becomes desirable to use more than one arm.

Conclusion:

Square field:

It is concluded that the arm should be positioned at a distance of $\frac{s}{\sqrt{2}}$ units away from the corners and the length of the arm is $\frac{s}{\sqrt{2}}$ .

Rectangular field:

It is concluded that the arm should be positioned at a distance of $\frac{\sqrt{l^2+w^2}}{2}$ units away from the corners and the length of the arm is $\frac{\sqrt{l^2+w^2}}{2}$ .

A circle is not circumscribed around a long rectangle with the diagonal as its diameter.Thus, it becomes desirable to use more than one arm.