Precalculus
9th Edition
ISBN: 9780321716835
Author: Michael Sullivan
Publisher: Addison Wesley
expand_more
expand_more
format_list_bulleted
Question
Chapter 1, Problem 23RE
To determine
To find: the center and radius of each circle and graph the circle.
Expert Solution & Answer
Answer to Problem 23RE
The center of the circle (h, k) is (1, -2) and the radius r is 3.
Explanation of Solution
Given:
x2+y2−2x+4y−4=0
Calculation:
Group the terms containing x and the terms containing y . Bring the constant to theright side of the equation.
(x2−2x)+(y2+4y)=4
Express the terms within the parentheses as perfect squares. Any number added on the left-hand side must be added on the right-hand side also.
(x2−2x+1)+(y2+4y+4)=4+1+4 ↑︷(22)2=1 ↑︷(42)2=4
Factor the expression.
(x−1)2+(y+2)2=32
The standard equation of a circle with center (h, k) and radius r is (x−h)2+(y−k)2=r2 .
Express the equation in standard form
(x−1)2+(y+2)2=32
Compare the equation with the standard form.
(x−h)2+(y− k)2= r2 ↓ ↓ ↓(x−1)2+(y−(−2))2=32
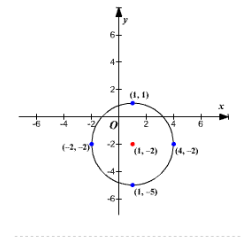
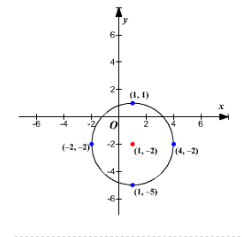
Therefore, the center of the circle (h, k) is (1, -2) and the radius r is 3.
The center of the circle is at the point (1, -2). Since the radius is 3 units, four points on the circle can be located by plotting points that are 3 units to the right, to the left, up, and down from the center. Use these points to graph the circle.
Substitute y=0 in the standard equation to find the x -intercept.
(x−1)2+(0+2)2= 9(x−1)2+ 4 = 9
Subtract 4 from both the sides.
(x−1)2+4−4=9−4 (x−1)2=5
Use the square root method.
x−1=±√5
Add 1 to both the sides.
x−1+1=±√5+1x=1±√5
The x -intercepts are 1+√5 and 1−√5 .
Substitute x=0 in the standard equation to find the y-intercept
(0−1)2+(y+2)2=91+(y+2)2=9
Subtract 1 from both the sides.
1+(y+2)2−1=9−1(y+2)2=8
Use the square root method.
y+2=±√8
Subtract 2 from both the sides.
y+2−2 = ±√8−2y=−2±√8
The y intercepts are −2+√8 and −2−√8 .
Conclusion:
Therefore, the center of the circle (h, k) is (1, -2) and the radius r is 3.
Chapter 1 Solutions
Precalculus
Ch. 1.1 - 1. On a real number line the origin is assigned...Ch. 1.1 - 2. If 3 and 5 are the coordinates of two points on...Ch. 1.1 - 3. If 3 and 4 are the legs of a right triangle,...Ch. 1.1 - 4. Use the converse of the Pythagorean Theorem to...Ch. 1.1 - 5. The area of a triangle whose base is b and...Ch. 1.1 - 6. True or False Two triangles are congruent if...Ch. 1.1 - 7. If ( x,y ) are the coordinates of a point P in...Ch. 1.1 - 8. The coordinate axes divide the xy-plane into...Ch. 1.1 - 9. If three distinct points P , Q and R all lie on...Ch. 1.1 - 10. True or False The distance between two points...
Ch. 1.1 - 11. True or False The point (1,4) lies in quadrant...Ch. 1.1 - 12. True or False The midpoint of a line segment...Ch. 1.1 - In Problems 15 and 16, plot each point in the...Ch. 1.1 - In Problems 15 and 16, plot each point in the...Ch. 1.1 - 17. Plot the points ( 2,0 ),( 2,3 ),( 2,4 ),(2,1)...Ch. 1.1 - 18. Plot the points ( 0,3 ),( 1,3 ),( 2,3 ),(5,3)...Ch. 1.1 - In Problems 35-46, find the distance d( P 1 , P 2...Ch. 1.1 - In Problems 35-46, find the distance d( P 1 , P 2...Ch. 1.1 - In Problems 35-46, find the distance d( P 1 , P 2...Ch. 1.1 - In Problems 35-46, find the distance d( P 1 , P 2...Ch. 1.1 - Prob. 21AYUCh. 1.1 - Prob. 22AYUCh. 1.1 - Prob. 23AYUCh. 1.1 - Prob. 24AYUCh. 1.1 - Prob. 25AYUCh. 1.1 - Prob. 26AYUCh. 1.1 - Prob. 27AYUCh. 1.1 - Prob. 28AYUCh. 1.1 - In Problems 51-56, plot each point and form the...Ch. 1.1 - In Problems 51-56, plot each point and form the...Ch. 1.1 - In Problems 51-56, plot each point and form the...Ch. 1.1 - In Problems 51-56, plot each point and form the...Ch. 1.1 - In Problems 51-56, plot each point and form the...Ch. 1.1 - In Problems 51-56, plot each point and form the...Ch. 1.1 - In Problems 57-64, find the midpoint of the line...Ch. 1.1 - In Problems 57-64, find the midpoint of the line...Ch. 1.1 - In Problemsfind the midpoint of the line segment...Ch. 1.1 - In Problems 3946 find the midpoint of the line...Ch. 1.1 - In Problems 3946 find the midpoint of the line...Ch. 1.1 - In Problems 57-64, find the midpoint of the line...Ch. 1.1 - In Problems 57-64, find the midpoint of the line...Ch. 1.1 - In Problems 57-64, find the midpoint of the line...Ch. 1.1 - If the point (2,5) is shifted 3 units to the right...Ch. 1.1 - If the point (1,6) is shifted 2 units to the left...Ch. 1.1 - Find all points having an-coordinate ofwhose...Ch. 1.1 - Find all points having a-coordinate ofwhose...Ch. 1.1 - Find all points on the x-axis that are 6 units...Ch. 1.1 - Find all points on the-axis that areunits from the...Ch. 1.1 - Suppose thatare the coordinates of a point in...Ch. 1.1 - Plot the pointsandin the-plane. Ifis the midpoint...Ch. 1.1 - The midpoint of the line segment from P1 to P2 is...Ch. 1.1 - The midpoint of the line segment fromtois. If,...Ch. 1.1 - The medians of a triangle are the line segments...Ch. 1.1 - An equilateral triangle is one in which all three...Ch. 1.1 - In Problems 103-106, find the length of each side...Ch. 1.1 - In Problems 103-106, find the length of each side...Ch. 1.1 - In Problems 103-106, find the length of each side...Ch. 1.1 - In Problems 103-106, find the length of each side...Ch. 1.1 - Baseball A major league baseball “diamond� is...Ch. 1.1 - Little league Baseball The layout of a Little...Ch. 1.1 - Baseball Refer to Problem 63. Overlay a...Ch. 1.1 - Little league Baseball Refer to Problem 64....Ch. 1.1 - Distance between Moving Objects A Ford Focus and a...Ch. 1.1 - Distance of a Moving Object from a Fixed Point A...Ch. 1.1 - Drafting Error When a draftsman draws three lines...Ch. 1.1 - Net Sales The figure illustrates the net sales...Ch. 1.1 - Poverty Threshold Poverty thresholds are...Ch. 1.1 - Write a paragraph that describes a Cartesian...Ch. 1.2 - Solve: 2( x+3 )1=7 (pp. A44-A46)Ch. 1.2 - Solve the equation x29=0Ch. 1.2 - The points, if any, at which a graph crosses or...Ch. 1.2 - The -intercepts of the graph of an equation are...Ch. 1.2 - Prob. 5AYUCh. 1.2 - Prob. 6AYUCh. 1.2 - Prob. 7AYUCh. 1.2 - True or False To find the y-intercepts of the...Ch. 1.2 - True or False The-coordinate of a point at which...Ch. 1.2 - True or False If a graph is symmetric with respect...Ch. 1.2 - In Problems, determine which of the given points...Ch. 1.2 - In Problems 1318, determine which of the given...Ch. 1.2 - In Problems, determine which of the given points...Ch. 1.2 - In Problems 1318, determine which of the given...Ch. 1.2 - In Problems 1318, determine which of the given...Ch. 1.2 - In Problems 1318, determine which of the given...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 11-22, find the intercepts and graph...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 23-32, plot each point. Then plot the...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - In Problems 33-44, the graph of an equation is...Ch. 1.2 - Prob. 51AYUCh. 1.2 - Prob. 52AYUCh. 1.2 - Prob. 53AYUCh. 1.2 - Prob. 54AYUCh. 1.2 - In Problems 5772, list the intercepts and test for...Ch. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems 5772, list the intercepts and test for...Ch. 1.2 - In Problems 5772, list the intercepts and test for...Ch. 1.2 - In Problems, list the intercepts and test for...Ch. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems, list the intercepts and test for...Ch. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems, list the intercepts and test for...Ch. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems 5772, list the intercepts and test for...Ch. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems 49-64, list the intercepts and test...Ch. 1.2 - In Problems 65-68, draw a quick sketch of each...Ch. 1.2 - In Problems 65-68, draw a quick sketch of each...Ch. 1.2 - In Problems 65-68, draw a quick sketch of each...Ch. 1.2 - In Problems 65-68, draw a quick sketch of each...Ch. 1.2 - Prob. 75AYUCh. 1.2 - Prob. 76AYUCh. 1.2 - Prob. 77AYUCh. 1.2 - Prob. 78AYUCh. 1.2 - Prob. 79AYUCh. 1.2 - If the graph of an equation is symmetric with...Ch. 1.2 - If the graph of an equation is symmetric with...Ch. 1.2 - If the graph of an equation is symmetric with...Ch. 1.2 - Microphones n studios and on stages, cardioid...Ch. 1.2 - Solar Energy The solar electric generating systems...Ch. 1.2 -
Graph,,and,noting which graphs are the...Ch. 1.2 - Explain what is meant by a complete graph.Ch. 1.2 - Draw a graph of an equation that contains two...Ch. 1.2 - Make up an equation with the intercepts,and....Ch. 1.2 - Draw a graph that contains the points ( 2,1 ) , (...Ch. 1.2 - Prob. 90AYUCh. 1.2 - Draw a graph that contains the points ( 2,5 ) , (...Ch. 1.2 - Prob. 92AYUCh. 1.2 - Prob. 93AYUCh. 1.2 - Prob. 94AYUCh. 1.3 - Prob. 1AYUCh. 1.3 - Prob. 2AYUCh. 1.3 - Prob. 3AYUCh. 1.3 - Prob. 4AYUCh. 1.3 - Prob. 5AYUCh. 1.3 - Prob. 6AYUCh. 1.3 - Prob. 7AYUCh. 1.3 - Prob. 8AYUCh. 1.3 - Prob. 9AYUCh. 1.3 - Prob. 10AYUCh. 1.3 - In Problems 13-16, (a) find the slope of the line...Ch. 1.3 - In Problems 13-16, (a) find the slope of the line...Ch. 1.3 - In Problems 13-16, (a) find the slope of the line...Ch. 1.3 - In Problems 13-16, (a) find the slope of the line...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 17-24, plot each pair of points and...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - In Problems 25-32, graph the line containing the...Ch. 1.3 - Prob. 29AYUCh. 1.3 - Prob. 30AYUCh. 1.3 - Prob. 31AYUCh. 1.3 - Prob. 32AYUCh. 1.3 - Prob. 33AYUCh. 1.3 - Prob. 34AYUCh. 1.3 - Prob. 35AYUCh. 1.3 - Prob. 36AYUCh. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 39-46, find an equation of the line L...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 5378, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 47-72, find an equation for the line...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 7998, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 7998, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 73-92, find the slope and y-intercept...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - In Problems 93—102, (a) find the intercepts of...Ch. 1.3 - Find an equation of the x-axis .Ch. 1.3 - Find an equation of the y-axis .Ch. 1.3 - In Problems 105-108, the equations of two lines...Ch. 1.3 - In Problems 105-108, the equations of two lines...Ch. 1.3 - In Problems 105-108, the equations of two lines...Ch. 1.3 - In Problems 105-108, the equations of two lines...Ch. 1.3 - In Problems, write an equation of each line....Ch. 1.3 - In Problems 115118, write an equation of each...Ch. 1.3 - In Problems 115118, write an equation of each...Ch. 1.3 - In Problems, write an equation of each line....Ch. 1.3 - Geometry Use slopes to show that the triangle...Ch. 1.3 - Geometry Use slopes to show that the quadrilateral...Ch. 1.3 - Geometry Use slopes to show that the quadrilateral...Ch. 1.3 - Geometry Use slopes and the distance formula to...Ch. 1.3 - Geometry Truck Rentals A truck rental company...Ch. 1.3 - Prob. 116AYUCh. 1.3 - Cost of Driving a Car The annual fixed costs of...Ch. 1.3 - Prob. 118AYUCh. 1.3 - Electricity Rates in Florida Florida Power &...Ch. 1.3 - Prob. 120AYUCh. 1.3 - Measuring Temperature The relationship between...Ch. 1.3 - Measuring Temperature The Kelvin scale for...Ch. 1.3 - Access Ramp A wooden access ramp is being built...Ch. 1.3 - U.S. Advertising Share A report showed that...Ch. 1.3 - Prob. 125AYUCh. 1.3 - Prob. 126AYUCh. 1.3 - Prob. 127AYUCh. 1.3 - Prob. 128AYUCh. 1.3 - Prob. 129AYUCh. 1.3 - Which of the following equations might have the...Ch. 1.3 - Prob. 131AYUCh. 1.3 - Prob. 132AYUCh. 1.3 - Prob. 133AYUCh. 1.3 - Prob. 134AYUCh. 1.3 - Carpentry Carpenters use the term pitch to...Ch. 1.3 - Prob. 136AYUCh. 1.3 - Prob. 137AYUCh. 1.3 - What can you say about two lines that have equal...Ch. 1.3 - Prob. 139AYUCh. 1.3 - Prob. 140AYUCh. 1.3 - Prob. 141AYUCh. 1.3 - Prob. 142AYUCh. 1.3 - Prob. 143AYUCh. 1.4 - In Problems 1-4, find the following for each pair...Ch. 1.4 - In Problems 1-4, find the following for each pair...Ch. 1.4 - In Problems 1-4, find the following for each pair...Ch. 1.4 - In Problems 1-4, find the following for each pair...Ch. 1.4 - 5. List the intercepts of the following graph.Ch. 1.4 - 6. Graph y= x 2 +15 using a graphing utility....Ch. 1.4 - Prob. 7AYUCh. 1.4 - Prob. 8AYUCh. 1.4 - Prob. 9AYUCh. 1.4 - Prob. 10AYUCh. 1.4 - Prob. 11AYUCh. 1.4 - Prob. 12AYUCh. 1.4 - Prob. 13AYUCh. 1.4 - Prob. 14AYUCh. 1.4 - Prob. 15AYUCh. 1.4 - Prob. 16AYUCh. 1.4 - Prob. 17AYUCh. 1.4 - Prob. 18AYUCh. 1.4 - Prob. 19AYUCh. 1.4 - Prob. 20AYUCh. 1.4 - Prob. 21AYUCh. 1.4 - Prob. 22AYUCh. 1.4 - Prob. 23AYUCh. 1.4 - Prob. 24AYUCh. 1.4 - Prob. 25AYUCh. 1.4 - Prob. 26AYUCh. 1.4 - Prob. 27AYUCh. 1.4 - Prob. 28AYUCh. 1.4 - Prob. 29AYUCh. 1.4 - Prob. 30AYUCh. 1.4 - Prob. 31AYUCh. 1.4 - Prob. 32AYUCh. 1.4 - Prob. 33AYUCh. 1.4 - Prob. 34AYUCh. 1.4 - Prob. 35AYUCh. 1.4 - Prob. 36AYUCh. 1.4 - Prob. 37AYUCh. 1.4 - Prob. 38AYUCh. 1.4 - Prob. 39AYUCh. 1.4 - Prob. 40AYUCh. 1.4 - Prob. 41AYUCh. 1.4 - Prob. 42AYUCh. 1.4 - In Problems 45-48, match each graph with the...Ch. 1.4 - In Problems 45-48, match each graph with the...Ch. 1.4 - In Problems 45-48, match each graph with the...Ch. 1.4 - In Problems 45-48, match each graph with the...Ch. 1.4 - Prob. 47AYUCh. 1.4 - Prob. 48AYUCh. 1.4 - Prob. 49AYUCh. 1.4 - Prob. 50AYUCh. 1.4 - Prob. 51AYUCh. 1.4 - Prob. 52AYUCh. 1.4 - Prob. 53AYUCh. 1.4 - Prob. 54AYUCh. 1.4 - Prob. 55AYUCh. 1.4 - Prob. 56AYUCh. 1.4 - Prob. 57AYUCh. 1.4 - Prob. 58AYUCh. 1.4 - Prob. 59AYUCh. 1.4 - Prob. 60AYUCh. 1.4 - Prob. 61AYUCh. 1.4 - Prob. 62AYUCh. 1.4 - Prob. 63AYUCh. 1.4 - Prob. 64AYUCh. 1.4 - Prob. 65AYUCh. 1 - Prob. 1RECh. 1 - Prob. 2RECh. 1 - Prob. 3RECh. 1 - Prob. 4RECh. 1 - Prob. 5RECh. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Prob. 9RECh. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Prob. 14RECh. 1 - Prob. 15RECh. 1 - Prob. 16RECh. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - Prob. 24RECh. 1 - Prob. 25RECh. 1 - Prob. 26RECh. 1 - Prob. 27RECh. 1 - Prob. 28RECh. 1 - Prob. 29RECh. 1 - Prob. 30RECh. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - Prob. 35RECh. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - Prob. 40RECh. 1 - Prob. 41RECh. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - Prob. 44RECh. 1 - Prob. 45RECh. 1 - Prob. 46RECh. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - Prob. 52RECh. 1 - Prob. 53RECh. 1 - In Problems , use and .
Find the distance from ...Ch. 1 - In Problems , use and .
Find the midpoint of...Ch. 1 - In Problems , use and .
(a) Find the slope of...Ch. 1 - In Problems , use and .
Graph by plotting...Ch. 1 - In Problems , use and .
Graph .
Ch. 1 - In Problems , use and .
List the intercepts and...Ch. 1 - In Problems , use and .
Write the...Ch. 1 - Prob. 8CTCh. 1 - Prob. 9CTCh. 1 - In Problems 13, use P1=(1,3) and P2=(5,1). For the...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Mathematical Connections Explain why a number and a numeral are considered different.
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
In hypothesis testing, the common level of significance is =0.05. Some might argue for a level of significance ...
Basic Business Statistics, Student Value Edition
1. combination of numbers, variables, and operation symbols is called an algebraic______.
Algebra and Trigonometry (6th Edition)
Piston compression A piston is seated at the top of a cylindrical chamber with radius 5 cm when it starts movin...
Calculus: Early Transcendentals (2nd Edition)
True or False The quotient of two polynomial expressions is a rational expression, (p. A35)
Precalculus
Product of the given expression.
Pre-Algebra Student Edition
Knowledge Booster
Similar questions
- 8:39 *** TEMU 5G 60% A ferris wheel is 28 meters in diameter and boarded from a platform that is 2 meters above the ground. The six o'clock position on the ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 4 minutes. The function h = f(t) gives your height in meters above the ground t minutes after the wheel begins to turn. What is the amplitude? 14 meters What is the equation of the Midline? y = 16 What is the period? 4 meters minutes The equation that models the height of the ferris wheel after t minutes is: f(t): = ƒ (3) = ·−14(0) + 16 syntax error: you gave an equation, not an expression. syntax error. Check your variables - you might be using an incorrect one. How high are you off of the ground after 3 minutes? Round your answe the nearest meter. ||| <arrow_forwardcan you solve this question step by step pleasearrow_forwardS cosx dx sin -3/ (x) Xarrow_forward
- The evolution of a population of Hippos, R(t), in hundreds, time in years, in an African National Park is given by the equation, dR dt (a) Solve the system exactly for R(t). = R(7 – R); R(0) = 3 2 (b) What happens as the time t → ∞o, i.e. what is the population a long time in the future? (c) Write an Euler scheme and compute until the population levels off (using Excel, Matlab, Octave, LibreCalc or similar). Do it twice, once with At = 0.1 and once with At = 0.05. (d) Plot all of your solutions on the same set of axes and comment.arrow_forwardfind For triangle ABC, with vertices A = (3,-1,2), B = (-5,4,-4) and C = (6, −1, −1), (a) the length of side AB, (b) the equation of the line that passes through A and B, (c) the angle at vertex B, (d) a vector perpendicular to the plane containing the triangle ABC, (e) the area of the triangle ABC. (f) the equation of a plane passing through A, B and C.arrow_forwardShowing all working, use the row reduction method to find the inverse of B, given by 5 -1 B = -3 1 3 1 -3 2arrow_forward
- Consider the matrix A, given by +63) A = 1 -3 4 -3 4 5 -105 (a) Find the determinant of the matrix, A. (b) Find all possible solutions, x, to the system Ax = b, where b is the column vector, (1,2, −4).arrow_forwardIf a (1,4,2) and b = (−1, −5,3), find |a|, a + b, 3a - 2b, a b, a x b and b × a. What is the angle between a and b?arrow_forwardShowing all working, find the eigenvalues and corresponding eigenvectors of -3 (a) (27) 6arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning