Chapter 1.1, Problem 65AYU

Drafting Error When a draftsman draws three lines that are to intersect at one point, the lines may not intersect as intended and subsequently will form an error triangle. If this error triangle is long and thin, one estimate for the location of the desired point is the midpoint of the shortest side. The figure shows one such error triangle.

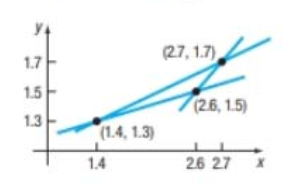
Find an estimate for the desired intersection point.

Find the distance from $\left(1.4,1.3\right)$ to the midpoint found in part $\left(a\right)$.

To determine

To calculate: An estimate for the desired intersection point.

Answer to Problem 65AYU

Solution:

The desired intersection point is $\left(2.65,1.6\right)$

Explanation of Solution

Given Information:

When a draftsman draws three lines that are to intersect at one point, the line may not intersect as intended and subsequently will form an error triangle. If this error triangle is long and thin, one estimate for the location of the desired point is the midpoint of the shortest side. The figure shows one such error triangle.

Formula used:

The midpoint formula: The coordinate of midpoint of two points $P_1=\left(x_1,y_1\right)$ and $P_2=\left(x_2,y_2\right)$ is $\left(x,y\right)=\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)$

Calculation:

The figure shows all the vertices of error triangle.

The desired intersection point is the midpoint of the shortest side. End points of the shortest side of error triangle are $\left(2.7,1.7\right)$ and $\left(2.6,1.5\right)$

Here, $P_1=\left(x_1,y_1\right)=\left(2.7,1.7\right)$ and $P_2=\left(x_2,y_2\right)=\left(2.6,1.5\right)$

By midpoint formula

$\left(x,y\right)=\left(\frac{2.7+2.6}{2},\frac{1.7+1.5}{2}\right)$

$\left(x,y\right)=\left(\frac{5.3}{2},\frac{3.2}{2}\right)$

$\left(x,y\right)=\left(2.65,1.6\right)$

Thus, the midpoint of the shortest side is $\left(2.65,1.6\right)$

Therefore, the desired intersection point is $\left(2.65,1.6\right)$

To determine

To calculate: The distance from the point $\left(1.4,1.3\right)$ to the midpoint of the shortest side $\left(2.65,1.6\right)$.

Answer to Problem 65AYU

Solution:

The distance from the point $\left(1.4,1.3\right)$ to the midpoint of the shortest side $\left(2.65,1.6\right)$ is $1.2855$

Explanation of Solution

Given Information:

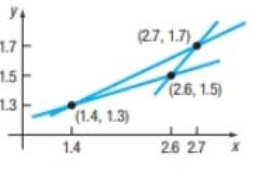
When a draftsman draws three lines that are to intersect at one point, the line may not intersect as intended and subsequently will form an error triangle. If this error triangle is long and thin, one estimate for the location of the desired point is the midpoint of the shortest side. The figure shows one such error triangle.

Formula used:

The distance formula: The distance between two points $P_1=(x_1,y_1)$ and $P_2=(x_2,y_2)$ denoted by $d\left(P_1,P_2\right)$, is $d\left(P_1,P_2\right)=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$

Calculation:

From part (a),

The midpoint of the shortest side is $\left(2.65,1.6\right)$

The opposite vertex of triangle is $\left(1.4,1.3\right)$

To find the distance from the point $\left(1.4,1.3\right)$ to point $\left(2.65,1.6\right)$,

By using the distance formula

$d=\sqrt{{\left(2.65-1.4\right)}^2+{\left(1.6-1.3\right)}^2}$

$d=\sqrt{{\left(1.25\right)}^2+{\left(0.3\right)}^2}$

$d=\sqrt{1.5625+0.09}$

$d=\sqrt{1.6525}$

$d\approx 1.2855$

Therefore, the distance between the right fielder to second base is approximately $1.2855$