Chapter 1.1, Problem 68AYU

Write a paragraph that describes a Cartesian plane. Then write a second paragraph that describes how to plot points in the Cartesian plane. Your paragraphs should include the terms “coordinate axes,� “ordered pair,� “coordinates,� “plot,� “ $x\text{-coordinate}$,� and “ $y\text{-coordinate}$.�

To determine

To write: A paragraph that describes a Cartesian plane. Then write a second paragraph that describes how to plot points in the Cartesian plane. Your paragraphs should include the terms “coordinate axes,” “ordered pair,” “coordinates,” “plot,” “$x-\mathrm{coordinate}$,” and “$y-\mathrm{coordinate}$”.

Answer to Problem 68AYU

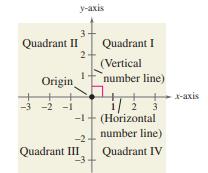
The Cartesian plane is formed by using two real number lines intersecting at right angles, as shown in Figure. The horizontal real number line is usually called the $x-axis$, and the vertical real number line is usually called the $y-axis$ . The point of intersection of these two axes is the origin, and the two axes divide the plane into four parts called quadrants.

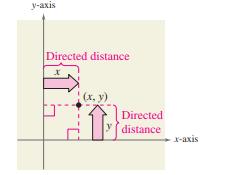
Each point in the plane corresponds to an ordered pair of real numbers and called coordinates of the point. The $x-\mathrm{coordinate}$ represents the directed distance from the -axis to the point, and the $y-\mathrm{coordinate}$ represents the directed distance from the -axis to the point, as shown in Figure.

Explanation of Solution

The Cartesian plane is formed by using two real number lines intersecting at right angles, as shown in Figure. The horizontal real number line is usually called the $x-axis$, and the vertical real number line is usually called the $y-axis$ . The point of intersection of these two axes is the origin, and the two axes divide the plane into four parts called quadrants.

Each point in the plane corresponds to an ordered pair of real numbers and called coordinates of the point. The $x-\mathrm{coordinate}$ represents the directed distance from the -axis to the point, and the $y-\mathrm{coordinate}$ represents the directed distance from the -axis to the point, as shown in Figure.

The notation denotes both a point in the plane and an open interval on the real number line.