Essential University Physics Volume 1, Loose Leaf Edition (4th Edition)
4th Edition
ISBN: 9780135264669
Author: Richard Wolfson
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 13, Problem 59P
A mass m is mounted between two springs with constants k1 and k2, as shown in Fig. 13.32. Show that the angular frequency of oscillation is
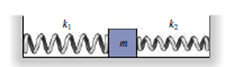
FIGURE 13.32 Problem 59
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The figure shows a uniform rod (length L = 2.36 m, mass = 1.9 kg) suspended from a pivot a distance
d = 0.27 m above its center of mass. The angular frequency (in rad/s) for small oscillations is:
axis
A simple pendulum is made of a 50 cm-string and a bob of mass m. At t = 0, the
pendulum is at its equilibrium position and is given an initial velocity v = 0.2 m/s.
The maximum angular speed, O'max, is:
O 0.2 rad/s
O 0.05 rad/s
O 0.1 rad/s
O 0.8 rad/s
O 0.4 rad/s
amplitude of the motion is A = 0.01 m and the mass of the block is m = 100 g
frequency w is equal to
A block-spring system has a maximum restoring force Fmax = 0.1 N. If the
the pendulum consists of a uniform disk with radius r = 10.0 cm and mass 500 g attached to a uniform rod with length L = 500 mm and mass 270 g. (a) Calculate the rotational inertia of the pendulum about the pivot point. (b) What is the distance between the pivot point and the center of mass of the pendulum? (c) Calculate the period of oscillation.
Chapter 13 Solutions
Essential University Physics Volume 1, Loose Leaf Edition (4th Edition)
Ch. 13.1 - A typical human heart rate is about 65 beats per...Ch. 13.2 - Two identical mass-spring systems are displaced...Ch. 13.3 - What happens to the period of a pendulum if (l)...Ch. 13.4 - Figure 13.18 shows the paths traced in the...Ch. 13.5 - Two different mass-spring systems are oscillating...Ch. 13.6 - The figure shows displacement-versus-time graphs...Ch. 13.7 - The photo shows a wineglass shattering in response...Ch. 13 - Is a vertically bouncing ball an example of...Ch. 13 - The vibration frequencies of molecules are much...Ch. 13 - What happens to the frequency of a simple harmonic...
Ch. 13 - If the spring of a simple harmonic oscillator is...Ch. 13 - How does the frequency of a simple harmonic...Ch. 13 - How would the frequency of a horizontal massspring...Ch. 13 - When in its cycle is the acceleration of an...Ch. 13 - Explain how simple harmonic motion might be used...Ch. 13 - One pendulum consists of a solid rod of mass m and...Ch. 13 - The x- and y-components of motion of a body are...Ch. 13 - Why is critical damping desirable in a cars...Ch. 13 - Explain why the frequency of a damped system is...Ch. 13 - Opera singers have been known to break glasses...Ch. 13 - What will happen to the period of a massspring...Ch. 13 - How can a system have more than one resonant...Ch. 13 - Prob. 16ECh. 13 - A violin string playing the note A oscillates at...Ch. 13 - The vibration frequency of a hydrogen chloride...Ch. 13 - Write expressions for the displacement x(t) in...Ch. 13 - The top of a skyscraper sways back and forth,...Ch. 13 - A hummingbirds wings vibrate at about 45 Hz. Whats...Ch. 13 - A 200-g mass is attached to a spring of constant k...Ch. 13 - An automobile suspension has an effective spring...Ch. 13 - The quartz crystal in a watch executes simple...Ch. 13 - A 342-g mass is attached to a spring and undergoes...Ch. 13 - A particle undergoes simple harmonic motion with...Ch. 13 - A particle undergoes simple harmonic motion with...Ch. 13 - How long should you make a simple pendulum so its...Ch. 13 - At the heart of a grandfather clock is a simple...Ch. 13 - A 622-g basketball with 24.0-cm diameter is...Ch. 13 - A meter stick is suspended from one end and set...Ch. 13 - A wheel rotates at 600 rpm. Viewed from the edge,...Ch. 13 - The x- and y-components of an objects motion are...Ch. 13 - A 450-g mass on a spring is oscillating at 1.2 Hz....Ch. 13 - A torsional oscillator of rotational inertia 1.6...Ch. 13 - Youre riding in a friends 1400-kg car with bad...Ch. 13 - The vibration of a piano string can be described...Ch. 13 - A massspring system has b/m = 0/5, where b is the...Ch. 13 - A cars front suspension has a natural frequency of...Ch. 13 - A simple model for carbon dioxide consists of...Ch. 13 - Two identical massspring systems consist of 430-g...Ch. 13 - The human eye and muscles that hold it can be...Ch. 13 - A mass m slides along a frictionless horizontal...Ch. 13 - Prob. 44PCh. 13 - A physics student, bored by a lecture on simple...Ch. 13 - A pendulum of length L is mounted in a rocket....Ch. 13 - The protein dynein powers the flagella that propel...Ch. 13 - A mass is attached to a vertical spring, which...Ch. 13 - Derive the period of a simple pendulum by...Ch. 13 - A solid disk of radius R is suspended from a...Ch. 13 - A thin steel beam is suspended from a crane and is...Ch. 13 - A cyclist turns her bicycle upside down to repair...Ch. 13 - An object undergoes simple harmonic motion in two...Ch. 13 - The muscles that drive insect wings minimize the...Ch. 13 - A pendulum consists of a 320-g solid ball 15.0 cm...Ch. 13 - If Jane and Tarzan are initially 8.0 m apart in...Ch. 13 - A small mass measuring device (SMMD) used for...Ch. 13 - A thin, uniform hoop of mass M and radius R is...Ch. 13 - A mass m is mounted between two springs with...Ch. 13 - The equation for an ellipse is (x2/a2) + (y2/b2) =...Ch. 13 - Show that the potential energy of a simple...Ch. 13 - The total energy of a massspring system is the sum...Ch. 13 - A solid cylinder of mass M and radius R is mounted...Ch. 13 - A mass m is free to slide on a frictionless track...Ch. 13 - A 250-g mass is mounted on a spring of constant k...Ch. 13 - A harmonic oscillator is underdamped if the...Ch. 13 - A massless spring with k = 74 N/m hangs from the...Ch. 13 - A meter stick is suspended from a frictionless rod...Ch. 13 - A particle of mass m has potential energy given by...Ch. 13 - Two balls with the same unknown mass m are mounted...Ch. 13 - Two mass-spring systems with the same mass are...Ch. 13 - Two mass-spring systems have the same mass and the...Ch. 13 - A 500-g mass is suspended from a thread 45 cm long...Ch. 13 - A 500-g block on a frictionless, horizontal...Ch. 13 - Repeat Problem 64 for a small solid ball of mass M...Ch. 13 - Youre working on the script of a movie whose plot...Ch. 13 - A 1.2-kg block rests on a frictionless surface and...Ch. 13 - A disk of radius R is suspended from a pivot...Ch. 13 - Prob. 79PCh. 13 - Youre a structural engineer working on a design...Ch. 13 - Show that x(t) = a cos t bsin t represents simple...Ch. 13 - Youre working for the summer with an ornithologist...Ch. 13 - While waiting for your plane to take off, you...Ch. 13 - Youre working for a playground equipment company,...Ch. 13 - Youve inherited your great-grandmothers mantle...Ch. 13 - This problem explores the nonlinear pendulum...Ch. 13 - Physicians and physiologists are interested in the...Ch. 13 - Physicians and physiologists are interested in the...Ch. 13 - Physicians and physiologists are interested in the...Ch. 13 - Physicians and physiologists are interested in the...
Additional Science Textbook Solutions
Find more solutions based on key concepts
1. What are the main organs of the skeletal system?
Human Anatomy & Physiology (2nd Edition)
Flask A contains yeast cells in glucose-minimal salts broth incubated at 30C with aeration. Flask B contains ye...
Microbiology: An Introduction
Match each of the following items with all the terms it applies to:
Human Physiology: An Integrated Approach (8th Edition)
Describe an example of bioconversion. What metabolic processes can result in fuels?
Microbiology: An Introduction
The number of named species is about __________, but the actual number of species on Earth is estimated to be a...
Biology: Life on Earth (11th Edition)
10.71 Identify each of the following as an acid or a base: (10.1)
H2SO4
RbOH
Ca(OH)2
HI
...
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- We do not need the analogy in Equation 16.30 to write expressions for the translational displacement of a pendulum bob along the circular arc s(t), translational speed v(t), and translational acceleration a(t). Show that they are given by s(t) = smax cos (smpt + ) v(t) = vmax sin (smpt + ) a(t) = amax cos(smpt + ) respectively, where smax = max with being the length of the pendulum, vmax = smax smp, and amax = smax smp2.arrow_forwardA grandfather clock has a pendulum length of 0.7 m and mass bob of 0.4 kg. A mass of 2 kg falls 0.8 m in seven days to keep the amplitude (from equilibrium) of the pendulum oscillation steady at 0.03 rad. What is the Q of the system?arrow_forwardThe angular position of a pendulum is represented by the equation = 0.032 0 cos t, where is in radians and = 4.43 rad/s. Determine the period and length of the pendulum.arrow_forward
- Determine the angular frequency of oscillation of a thin, uniform, vertical rod of mass m and length L pivoted at the point O and connected to two springs (Fig. P16.78). The combined spring constant of the springs is k(k = k1 + k2), and the masses of the springs are negligible. Use the small-angle approximation (sin ). FIGURE P16.78arrow_forwardA watch balance wheel (Fig. P15.25) has a period of oscillation of 0.250 s. The wheel is constructed so that its mass of 20.0 g is concentrated around a rim of radius 0.500 cm. What are (a) the wheels moment of inertia and (b) the torsion constant of the attached spring? Figure P15.23arrow_forwardA 50.0-g object connected to a spring with a force constant of 35.0 N/m oscillates with an amplitude of 4.00 cm on a frictionless, horizontal surface. Find (a) the total energy of the system and (b) the speed of the object when its position is 1.00 cm. Find (c) the kinetic energy and (d) the potential energy when its position is 3.00 cm.arrow_forward
- A nylon siring has mass 5.50 g and length L = 86.0 cm. The lower end is tied to the floor, and the upper end is tied to a small set of wheels through a slot in a track on which the wheels move (Fig. P18.76). The wheels have a mass that is negligible compared with that of the siring, and they roll without friction on the track so that the upper end of the string is essentially free. Figure P18.76 At equilibrium, the string is vertical and motionless. When it is carrying a small-amplilude wave, you may assume the string is always under uniform tension 1.30 N. (a) Find the speed of transverse waves on the siring, (b) The string's vibration possibilities are a set of standing-wave states, each with a node at the fixed bottom end and an antinode at the free top end. Find the node-antinode distances for each of the three simplest states, (c) Find the frequency of each of these states.arrow_forwardThe amplitude of a lightly damped oscillator decreases by 3.0% during each cycle. What percentage of the mechanical energy of the oscillator is lost in each cycle?arrow_forwardWhat conditions must be met to produce SHM?arrow_forward
- Which of the following statements is not true regarding a massspring system that moves with simple harmonic motion in the absence of friction? (a) The total energy of the system remains constant. (b) The energy of the system is continually transformed between kinetic and potential energy. (c) The total energy of the system is proportional to the square of the amplitude. (d) The potential energy stored in the system is greatest when the mass passes through the equilibrium position. (e) The velocity of the oscillating mass has its maximum value when the mass passes through the equilibrium position.arrow_forwardA block of unknown mass is attached to a spring with a spring constant of 6.50 N/m and undergoes simple harmonic motion with an amplitude of 10.0 cm. When the block is halfway between its equilibrium position and the end point, its speed is measured to be 30.0 cm/s. Calculate (a) the mass of the block, (b) the period of the motion, and (c) the maximum acceleration of the block.arrow_forwardIn an engine, a piston oscillates with simple harmonic motion so that its position varies according to the expression x=5.00cos(2t+6) where x is in centimeters and t is in seconds. At t = 0, find (a) the position of the piston, (b) its velocity, and (c) its acceleration. Find (d) the period and (e) the amplitude of the motion.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
Classical Dynamics of Particles and Systems
Physics
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
SIMPLE HARMONIC MOTION (Physics Animation); Author: EarthPen;https://www.youtube.com/watch?v=XjkUcJkGd3Y;License: Standard YouTube License, CC-BY