Essential University Physics Volume 1, Loose Leaf Edition (4th Edition)
4th Edition
ISBN: 9780135264669
Author: Richard Wolfson
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 13, Problem 63P
A solid cylinder of mass M and radius R is mounted on an axle through its center. The axle is attached to a horizontal spring of constant k, and the cylinder rolls back and forth without slipping (Fig. 13.33). Write the statement of energy conservation for this system, and differentiate it to obtain an equation analogous to Equation 13.3 (see Problem 62). Comparing your result with Equation 13.3, determine the angular frequency of the motion.
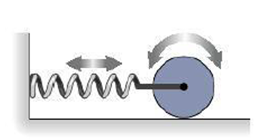
FIGURE 13.33 Problem 63
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A solid cylinder of mass M and radius R is mounted to an axle through its center. The axle is attached to a horizontal spring of constant k, as shown in the figure. Initially the cylinder is at rest and the spring is un-stretched. The cylinder is then pulled a distance A and released. The cylinder rolls back and forth without slipping.
A) Determine the angular frequency ωfreq and period T of the simple harmonic motion of this spring-rolling mass system? Express your answer in terms of k and M.
B) Assume that we have the same spring and mass system, onlynow the cylinder is released from rest on a frictionless surface at a distance A from the equilibrium position. What is the period of the simple harmonic motion of this system? Express your answer in terms of k and M.
An object is undergoing simple harmonic motion along the x-axis. Its position is described as a function of time by x(t) = 1.1 cos(3.4t – 1.9), where x is in meters, the time, t, is in seconds, and the argument of the cosine is in radians.
Find the amplitude of the simple harmonic motion, in meters.
What is the value of the angular frequency, in radians per second?
Determine the position of the object, in meters, at the time t = 0.
What is the object’s velocity, in meters per second, at time t = 0?
Calculate the object’s acceleration, in meters per second squared, at time t = 0.
What is the magnitude of the object’s maximum acceleration, in meters per second squared?
A door stopper spring is held at an angle from its equilibrium position and then released, and the angular
velocity of the plastic end is given by the function:
w (t) =
10e-0.1t
cos(5t)
1. Find its angular acceleration function a (t).
2. Find its angular displacement function 0 (t), assuming 0 (0) = 0.
3. If the rotational motion is confined to the xy plane, what is the direction of the acceleration at t=0?
Justify your answers with your rationale and equations used.
Chapter 13 Solutions
Essential University Physics Volume 1, Loose Leaf Edition (4th Edition)
Ch. 13.1 - A typical human heart rate is about 65 beats per...Ch. 13.2 - Two identical mass-spring systems are displaced...Ch. 13.3 - What happens to the period of a pendulum if (l)...Ch. 13.4 - Figure 13.18 shows the paths traced in the...Ch. 13.5 - Two different mass-spring systems are oscillating...Ch. 13.6 - The figure shows displacement-versus-time graphs...Ch. 13.7 - The photo shows a wineglass shattering in response...Ch. 13 - Is a vertically bouncing ball an example of...Ch. 13 - The vibration frequencies of molecules are much...Ch. 13 - What happens to the frequency of a simple harmonic...
Ch. 13 - If the spring of a simple harmonic oscillator is...Ch. 13 - How does the frequency of a simple harmonic...Ch. 13 - How would the frequency of a horizontal massspring...Ch. 13 - When in its cycle is the acceleration of an...Ch. 13 - Explain how simple harmonic motion might be used...Ch. 13 - One pendulum consists of a solid rod of mass m and...Ch. 13 - The x- and y-components of motion of a body are...Ch. 13 - Why is critical damping desirable in a cars...Ch. 13 - Explain why the frequency of a damped system is...Ch. 13 - Opera singers have been known to break glasses...Ch. 13 - What will happen to the period of a massspring...Ch. 13 - How can a system have more than one resonant...Ch. 13 - Prob. 16ECh. 13 - A violin string playing the note A oscillates at...Ch. 13 - The vibration frequency of a hydrogen chloride...Ch. 13 - Write expressions for the displacement x(t) in...Ch. 13 - The top of a skyscraper sways back and forth,...Ch. 13 - A hummingbirds wings vibrate at about 45 Hz. Whats...Ch. 13 - A 200-g mass is attached to a spring of constant k...Ch. 13 - An automobile suspension has an effective spring...Ch. 13 - The quartz crystal in a watch executes simple...Ch. 13 - A 342-g mass is attached to a spring and undergoes...Ch. 13 - A particle undergoes simple harmonic motion with...Ch. 13 - A particle undergoes simple harmonic motion with...Ch. 13 - How long should you make a simple pendulum so its...Ch. 13 - At the heart of a grandfather clock is a simple...Ch. 13 - A 622-g basketball with 24.0-cm diameter is...Ch. 13 - A meter stick is suspended from one end and set...Ch. 13 - A wheel rotates at 600 rpm. Viewed from the edge,...Ch. 13 - The x- and y-components of an objects motion are...Ch. 13 - A 450-g mass on a spring is oscillating at 1.2 Hz....Ch. 13 - A torsional oscillator of rotational inertia 1.6...Ch. 13 - Youre riding in a friends 1400-kg car with bad...Ch. 13 - The vibration of a piano string can be described...Ch. 13 - A massspring system has b/m = 0/5, where b is the...Ch. 13 - A cars front suspension has a natural frequency of...Ch. 13 - A simple model for carbon dioxide consists of...Ch. 13 - Two identical massspring systems consist of 430-g...Ch. 13 - The human eye and muscles that hold it can be...Ch. 13 - A mass m slides along a frictionless horizontal...Ch. 13 - Prob. 44PCh. 13 - A physics student, bored by a lecture on simple...Ch. 13 - A pendulum of length L is mounted in a rocket....Ch. 13 - The protein dynein powers the flagella that propel...Ch. 13 - A mass is attached to a vertical spring, which...Ch. 13 - Derive the period of a simple pendulum by...Ch. 13 - A solid disk of radius R is suspended from a...Ch. 13 - A thin steel beam is suspended from a crane and is...Ch. 13 - A cyclist turns her bicycle upside down to repair...Ch. 13 - An object undergoes simple harmonic motion in two...Ch. 13 - The muscles that drive insect wings minimize the...Ch. 13 - A pendulum consists of a 320-g solid ball 15.0 cm...Ch. 13 - If Jane and Tarzan are initially 8.0 m apart in...Ch. 13 - A small mass measuring device (SMMD) used for...Ch. 13 - A thin, uniform hoop of mass M and radius R is...Ch. 13 - A mass m is mounted between two springs with...Ch. 13 - The equation for an ellipse is (x2/a2) + (y2/b2) =...Ch. 13 - Show that the potential energy of a simple...Ch. 13 - The total energy of a massspring system is the sum...Ch. 13 - A solid cylinder of mass M and radius R is mounted...Ch. 13 - A mass m is free to slide on a frictionless track...Ch. 13 - A 250-g mass is mounted on a spring of constant k...Ch. 13 - A harmonic oscillator is underdamped if the...Ch. 13 - A massless spring with k = 74 N/m hangs from the...Ch. 13 - A meter stick is suspended from a frictionless rod...Ch. 13 - A particle of mass m has potential energy given by...Ch. 13 - Two balls with the same unknown mass m are mounted...Ch. 13 - Two mass-spring systems with the same mass are...Ch. 13 - Two mass-spring systems have the same mass and the...Ch. 13 - A 500-g mass is suspended from a thread 45 cm long...Ch. 13 - A 500-g block on a frictionless, horizontal...Ch. 13 - Repeat Problem 64 for a small solid ball of mass M...Ch. 13 - Youre working on the script of a movie whose plot...Ch. 13 - A 1.2-kg block rests on a frictionless surface and...Ch. 13 - A disk of radius R is suspended from a pivot...Ch. 13 - Prob. 79PCh. 13 - Youre a structural engineer working on a design...Ch. 13 - Show that x(t) = a cos t bsin t represents simple...Ch. 13 - Youre working for the summer with an ornithologist...Ch. 13 - While waiting for your plane to take off, you...Ch. 13 - Youre working for a playground equipment company,...Ch. 13 - Youve inherited your great-grandmothers mantle...Ch. 13 - This problem explores the nonlinear pendulum...Ch. 13 - Physicians and physiologists are interested in the...Ch. 13 - Physicians and physiologists are interested in the...Ch. 13 - Physicians and physiologists are interested in the...Ch. 13 - Physicians and physiologists are interested in the...
Additional Science Textbook Solutions
Find more solutions based on key concepts
17. What is the tension in the rope of Figure EX7.17?
Figure EX7.17
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
18. SCIENTIFIC THINKING By measuring the fossil remains of Homo floresiensis, scientists have estimated its wei...
Campbell Biology: Concepts & Connections (9th Edition)
Level 2: Application/Analysis 4. Nitrifying bactcria participatc in the nitrogen cycle mainly by (A) converting...
Campbell Biology (11th Edition)
Explain all answers clearly, with complete sentences and proper essay structure if needed. An asterisk (*) desi...
Cosmic Perspective Fundamentals
Modified True/False 6. __________ Halophiles inhabit extremely saline habitats, such as the Great Salt Lake.
Microbiology with Diseases by Body System (5th Edition)
3. What are serous membranes, and what are their functions?
Human Anatomy & Physiology (2nd Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A surfboard of mass S rests on a frictionless surface. The surfboard is attached to a spring (constant K) which is in turn attached to an immobile wall. The surfboard is displaced a distance of C from equilibrium and then is released. If I double the initial amplitude to 2C, what will the new angular frequency of oscillation (omega2) be?arrow_forwardThe pendulum in the figure consists of a uniform disk with radius r = 15.0 cm and mass 880 g attached to a uniform rod with length L = 570 mm and mass 270 g. (a) Calculate the rotational inertia of the pendulum about the pivot point. (b) What is the distance between the pivot point and the center of mass of the pendulum? (c) Calculate the period of oscillation. L.arrow_forwardanswer in paper please. Book reference : university physics with modern physics 13th editionarrow_forward
- The figure below shows a piston from your car engine. Don't worry, you will not be required to understand an internal combustion engine for this problem. Instead, we simply notice that the up/down motion of the piston is exactly described as Simple Harmonic Motion. The tachometer on your dashboard tells you that your engine is turning at w = 1660 rpm (revolutions/minute). The owner's manual for your car tells you that the amplitude of the motion of the piston is Ymax = A = 0.099 meters. Simple Harmonic Motion wrist pin 500 grams Crankshaft A (top of stroke) B (midpoint) -C (bottom of stroke) y=-A y=+A Determine all the following: The angular frequency in proper units w = The period of the piston, T = The frequency of the piston, f = The maximum velocity of the piston, Vmax = meters/sec The piston velocity when y = 58% of full stroke, v(y = 0.58 Ymax) = seconds Hz rad/sec meters/secarrow_forwardAn airplane engine and the pylon that attaches it to the wing are idealized as shown below. Drive the equation of motion for small oscillations. Neglect damping and assume free vibration. The rotational spring shown exerts a restoring moment on the pylon (beam ) which is proportional to the angle the pylon makes with the vertical. The engine has a mass moment of inertia la about an axis through its mass center. Assume that the pylon(beam) is rigid and weightless. Solve this problem in terms of: - la, mass moment of inertia of the engine about its own centroid - W, weight of the engine - K., rotational spring constant L, length of the pylon LOTATIAL SPAINGarrow_forwardA door stopper spring is flicked from its equilibrium position, and the angular velocity of the plastic end is given by the function: o (t) = 5e-0.21t sin(4t) 1. Find its angular acceleration function a (t). 2. Find its angular displacement function 0 (t), assuming 0 (0) = 0. 3. If the rotational motion is confined to the xy plane, what is the direction of the acceleration at t=0? Justify your answers with your rationale and equations used.arrow_forward
- Consider the statement E = E En, with E the energy of the system and E, ox whA, the energy in the nth mode of ocillation, which has angular frequency wn and amplitude An. It was true in the linear case. Which of the statements below are true when it comes to non-linear oscillations? The expression still works, what changes is the independence of the modes. It is still true in the non-linear case. O The only difference is that the amplitude in each mode depends on the energies in the other modes. O The expression still works. We just need to take into account the non-linear interactions between modes in the system to compute the energy in each mode at the beginning, and then we have solved the problem for all times. O It isn't valid in the non-linear case anymorearrow_forwardA uniform rod of mass M and length L is free to swing back and forth by pivoting a distance x from its center. It undergoes harmonic oscillations by swinging back and forth under the influence of gravity. M = 4.6 kgL = 1.5 mx = 0.24 m a. In terms of M, L, and x, what is the rod’s moment of inertia I about the pivot point. b. Calculate the rod’s period T in seconds for small oscillations about its pivot point. c. In terms of L, find an expression for the distance xm for which the period is a minimum.arrow_forwardA uniform solid cylinder of mass M=0.5 kg and radius R = 3 cm is attached to a massless spring of spring constant k = 30 N/m, as shown in the figure. The cylinder can roll without slip on the horizontal surface. If the system is set to motion from rest when the spring is stretched by 2 cm, the center of mass of the cylinder undergoes a simple harmonic motion. What is the period of the system. (ICM = ½ MR2) %3D %3D %3D M k 22arrow_forward
- You have made a physical pendulum by swinging a rod of mass M = 1.08 kg and length L = 1.45 meters around its end. The mass of the rod is distributed uniformly along its length. We will assume that the amplitude of the swing is max = 19.34 degrees. Solid Rod Swings in Simple Harmonic Motion ^ 0=-0, max 0=+0₁ max Determine all the following: The FORMULA for the moment of inertia of your rod, I = The distance from the pivot point to the Center-Of-Mass, d = The angular frequency of the pendulum, w = The amplitude of the motion in radians, max = radians The angular velocity when 0 = 64% of full swing, w(0 = 0.64 0max): NOTE: The first question requires a FORMULA, not a value. rad/sec = meters rad/secarrow_forwardA physical pendulum consists of a disk of radius R = 2 m, whose mass is homogeneously distributed and is equal to 6 kg, is suspended just at a point on its perimeter. The puck is displaced from its equilibrium position. until it forms an angle θ = π/16 with respect to the vertical and is then released. find: a) The period of the system. b) Make a graph of angular position v/s time where the amplitude, initial phase and system period.arrow_forwardA wheel is free to rotate about its fixed axle. A spring is attached to one of its spokes at distance r from the axle. Assuming that the wheel is a hoop of mass m and radius R, what is the angular frequency w of small oscillations of this system in terms of m, R, r, and the srping constant k? What is w if r =R and if r = 0? Thank you for the help. I think I'm tripping myself up with using r in the equations.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON
Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON
SIMPLE HARMONIC MOTION (Physics Animation); Author: EarthPen;https://www.youtube.com/watch?v=XjkUcJkGd3Y;License: Standard YouTube License, CC-BY