Chapter 13, Problem 23ICA

As a reminder, the Reynolds number is discussed in Chapter 9. Dimensionless Number.

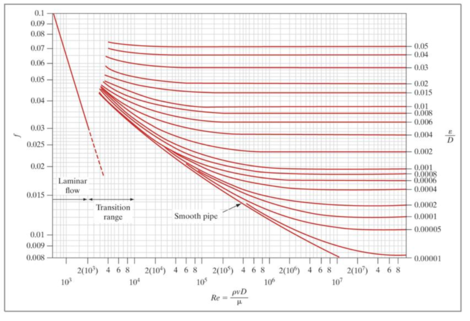
When discussing the flow of a fluid through a piping system, we say that friction occurs between the fluid and the pipe wall due to viscous drag. The loss of energy due to the friction against the pipe wall is described by the friction factor. The Darcy friction factor (f) was developed by Henry Darcy (1803–1858), a French scientist who made several important contributions to the field of hydraulics. The friction factor depends on several other factors, including flow regime, Reynolds number, and pipe roughness. The friction factor can be determined in several ways, including from the Moody diagram (show below).

Olive oil having a specific gravity of 0.914 and viscosity of 100.8 centipoise is draining by gravity from the bottom of a tank. The drain line from the tank is a 4-diameter pipe made of commercial steel (pipe roughness, ε=0.045 millimeters). The velocity is 11 meters per second. Determine the friction factor for this system, using the following process.

Step 1: Determine the Reynolds number: $\mathrm{Re}=\frac{\rho \upsilon D}{\mu }$.

Step 2: Determine flow regima.

• If the flow is laminar (Re £ 2000), continue with step 3.
• If the flow is turbulent or transitional (Re > 2000), continue with step 3.

Step 3: Determine the relative roughness ratio: (ε/D).

Step 4: Determine the Darcy friction factor (f) from the diagram.

ICA 13-23

Repeat ICA 13-22 with the following conditions:

Lactic acid, with a specific gravity of 1.249 and dynamic viscosity of 40.33 centipoise, is flowing in a $1\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$-inch-diameter galvanized iron pipe at a velocity of 1.5 meters per second. Assume the pipe roughness (ε) of galvanized iron is 0.006 inches. Determine the friction factor for this system.