Vector Mechanics for Engineers: Statics and Dynamics
11th Edition
ISBN: 9780073398242
Author: Ferdinand P. Beer, E. Russell Johnston Jr., David Mazurek, Phillip J. Cornwell, Brian Self
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 12.2, Problem 12.92P
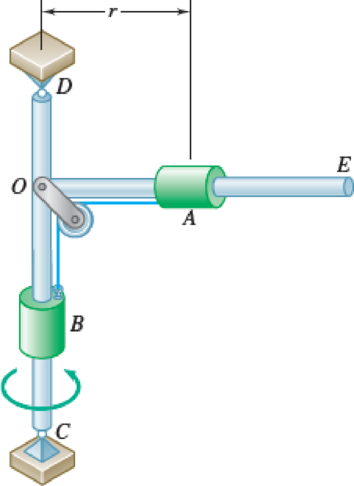
Two 2.6-lb collars A and B can slide without friction on a frame, consisting of the horizontal rod OE and the vertical rod CD, which is free to rotate about CD. The two collars are connected by a cord running over a pulley that is attached to the frame at O, and a stop prevents
Fig. P12.92
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Continuity equation
A
y
x
dx
D
T
معادلة الاستمرارية
Ly
X
Q/Prove that
ди
хе
+ ♥+ ㅇ?
he
me
ze
ོ༞“༠ ?
Q
Derive (continuity equation)?
I want to derive clear mathematics.
motor supplies 200 kW at 6 Hz to flange A of the shaft shown in Figure. Gear B transfers 125 W of power to operating machinery in the factory, and the remaining power in the shaft is mansferred by gear D. Shafts (1) and (2) are solid aluminum (G = 28 GPa) shafts that have the same diameter and an allowable shear stress of t= 40 MPa. Shaft (3) is a solid steel (G = 80 GPa) shaft with an allowable shear stress of t = 55 MPa. Determine:
a) the minimum permissible diameter for aluminum shafts (1) and (2)
b) the minimum permissible diameter for steel shaft (3).
c) the rotation angle of gear D with respect to flange A if the shafts have the minimum permissible diameters as determined in (a) and (b).
Chapter 12 Solutions
Vector Mechanics for Engineers: Statics and Dynamics
Ch. 12.1 - A 1000-lb boulder B is resting on a 200-lb...Ch. 12.1 - Marble A is placed in a hollow tube, and the tube...Ch. 12.1 - The two systems shown start from rest. On the...Ch. 12.1 - Blocks A and B are released from rest in the...Ch. 12.1 - People sit on a Ferris wheel at points A, B, C,...Ch. 12.1 - Crate A is gently placed with zero initial...Ch. 12.1 - Two blocks weighing WA and WB are at rest on a...Ch. 12.1 - Objects A, B, and C have masses mA, mB, and mC,...Ch. 12.1 - Prob. 12.4FBPCh. 12.1 - Blocks A and B have masses mA and mB,...
Ch. 12.1 - A pilot of mass m flies a jet in a half-vertical...Ch. 12.1 - Wires AC and BC are attached to a sphere that...Ch. 12.1 - A collar of mass m is attached to a spring and...Ch. 12.1 - Prob. 12.9FBPCh. 12.1 - At the instant shown, the length of the boom AB is...Ch. 12.1 - Disk A rotates in a horizontal plane about a...Ch. 12.1 - Pin B has a mass m and slides along the slot in...Ch. 12.1 - Prob. 12.1PCh. 12.1 - Prob. 12.2PCh. 12.1 - Prob. 12.3PCh. 12.1 - Prob. 12.4PCh. 12.1 - Prob. 12.5PCh. 12.1 - Prob. 12.6PCh. 12.1 - A tugboat pulls a small barge through a harbor....Ch. 12.1 - Prob. 12.8PCh. 12.1 - 12.9 If an automobile’s braking distance from 90...Ch. 12.1 - Prob. 12.10PCh. 12.1 - The coefficients of friction between the load and...Ch. 12.1 - A light train made up of two cars is traveling at...Ch. 12.1 - Prob. 12.13PCh. 12.1 - Prob. 12.14PCh. 12.1 - Prob. 12.15PCh. 12.1 - Prob. 12.16PCh. 12.1 - A 5000-lb truck is being used to lift a 1000-lb...Ch. 12.1 - Block A has a mass of 40 kg, and block B has a...Ch. 12.1 - Block A has a mass of 40 kg, and block B has a...Ch. 12.1 - The flat-bed trailer carries two 1500-kg beams...Ch. 12.1 - 12.21 A baggage conveyor is used to unload luggage...Ch. 12.1 - To unload a bound stack of plywood from a truck,...Ch. 12.1 - To transport a series of bundles of shingles A to...Ch. 12.1 - An airplane has a mass of 25 Mg and its engines...Ch. 12.1 - Prob. 12.25PCh. 12.1 - A constant force P is applied to a piston and rod...Ch. 12.1 - A spring AB of constant k is attached to a support...Ch. 12.1 - Block A has a mass of 10 kg, and blocks B and C...Ch. 12.1 - Prob. 12.29PCh. 12.1 - Prob. 12.30PCh. 12.1 - A 10-lb block B rests as shown on a 20-lb bracket...Ch. 12.1 - Knowing that k = 0.30, determine the acceleration...Ch. 12.1 - Knowing that k = 0.30, determine the acceleration...Ch. 12.1 - Prob. 12.34PCh. 12.1 - Block B of mass 10 kg rests as shown on the upper...Ch. 12.1 - Prob. 12.36PCh. 12.1 - Prob. 12.37PCh. 12.1 - Human centrifuges are often used to simulate...Ch. 12.1 - A single wire ACB passes through a ring at C...Ch. 12.1 - Prob. 12.41PCh. 12.1 - Prob. 12.42PCh. 12.1 - Prob. 12.43PCh. 12.1 - Prob. 12.44PCh. 12.1 - During a high-speed chase, a 2400-lb sports car...Ch. 12.1 - An airline pilot climbs to a new flight level...Ch. 12.1 - The roller-coaster track shown is contained in a...Ch. 12.1 - A spherical-cap governor is fixed to a vertical...Ch. 12.1 - A series of small packages, each with a mass of...Ch. 12.1 - 12.50 A 54-kg pilot flies a jet trainer in a...Ch. 12.1 - Prob. 12.51PCh. 12.1 - A curve in a speed track has a radius of 1000 ft...Ch. 12.1 - Tilting trains, such as the Acela Express that...Ch. 12.1 - Prob. 12.54PCh. 12.1 - A 3-kg block is at rest relative to a parabolic...Ch. 12.1 - Prob. 12.56PCh. 12.1 - A turntable A is built into a stage for use in a...Ch. 12.1 - The carnival ride from Prob. 12.51 is modified so...Ch. 12.1 - Prob. 12.59PCh. 12.1 - Prob. 12.60PCh. 12.1 - A small block B fits inside a slot cut in arm OA...Ch. 12.1 - The parallel-link mechanism ABCD is used to...Ch. 12.1 - Prob. 12.63PCh. 12.1 - A small 250-g collar C can slide on a semicircular...Ch. 12.1 - A small 250-g collar C can slide on a semicircular...Ch. 12.1 - An advanced spatial disorientation trainer is...Ch. 12.1 - The 3-kg collar B slides on the frictionless arm...Ch. 12.1 - A 0.5-kg block B slides without friction inside a...Ch. 12.1 - Pin B weighs 4 oz and is free to slide in a...Ch. 12.1 - Prob. 12.71PCh. 12.1 - Prob. 12.72PCh. 12.2 - A particle of mass m is projected from point A...Ch. 12.2 - A particle of mass m is projected from point A...Ch. 12.2 - Determine the mass of the earth knowing that the...Ch. 12.2 - Show that the radius r of the moons orbit can be...Ch. 12.2 - Communication satellites are placed in a...Ch. 12.2 - Prob. 12.81PCh. 12.2 - The orbit of the planet Venus is nearly circular...Ch. 12.2 - A satellite is placed into a circular orbit about...Ch. 12.2 - The periodic time (see Prob. 12.83) of an earth...Ch. 12.2 - A 500-kg spacecraft first is placed into a...Ch. 12.2 - A space vehicle is in a circular orbit of 2200-km...Ch. 12.2 - Prob. 12.87PCh. 12.2 - Prob. 12.88PCh. 12.2 - Prob. 12.89PCh. 12.2 - A 1-kg collar can slide on a horizontal rod that...Ch. 12.2 - Two 2.6-lb collars A and B can slide without...Ch. 12.2 - A small ball swings in a horizontal circle at the...Ch. 12.3 - A uniform crate C with mass mC is being...Ch. 12.3 - A uniform crate C with mass m is being transported...Ch. 12.3 - Prob. 12.94PCh. 12.3 - Prob. 12.95PCh. 12.3 - A particle with a mass m describes the path...Ch. 12.3 - A particle of mass m describes the parabola y =...Ch. 12.3 - Prob. 12.98PCh. 12.3 - Prob. 12.99PCh. 12.3 - Prob. 12.100PCh. 12.3 - Prob. 12.101PCh. 12.3 - A satellite describes an elliptic orbit about a...Ch. 12.3 - Prob. 12.103PCh. 12.3 - Prob. 12.104PCh. 12.3 - Prob. 12.105PCh. 12.3 - Halleys comet travels in an elongated elliptic...Ch. 12.3 - Prob. 12.109PCh. 12.3 - A space probe is to be placed in a circular orbit...Ch. 12.3 - The Clementine spacecraft described an elliptic...Ch. 12.3 - A space probe is describing a circular orbit of...Ch. 12.3 - Prob. 12.115PCh. 12.3 - A space shuttle is describing a circular orbit at...Ch. 12.3 - Prob. 12.117PCh. 12.3 - A satellite describes an elliptic orbit about a...Ch. 12.3 - Prob. 12.119PCh. 12.3 - Prob. 12.120PCh. 12.3 - Show that the angular momentum per unit mass h of...Ch. 12 - In the braking test of a sports car, its velocity...Ch. 12 - A bucket is attached to a rope of length L = 1.2 m...Ch. 12 - A 500-lb crate B is suspended from a cable...Ch. 12 - The parasailing system shown uses a winch to pull...Ch. 12 - Prob. 12.128RPCh. 12 - Telemetry technology is used to quantify kinematic...Ch. 12 - The radius of the orbit of a moon of a given...Ch. 12 - Prob. 12.131RPCh. 12 - Prob. 12.132RPCh. 12 - Disk A rotates in a horizontal plane about a...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- First monthly exam Gas dynamics Third stage Q1/Water at 15° C flow through a 300 mm diameter riveted steel pipe, E-3 mm with a head loss of 6 m in 300 m length. Determine the flow rate in pipe. Use moody chart. Q2/ Assume a car's exhaust system can be approximated as 14 ft long and 0.125 ft-diameter cast-iron pipe ( = 0.00085 ft) with the equivalent of (6) regular 90° flanged elbows (KL = 0.3) and a muffler. The muffler acts as a resistor with a loss coefficient of KL= 8.5. Determine the pressure at the beginning of the exhaust system (pl) if the flowrate is 0.10 cfs, and the exhaust has the same properties as air.(p = 1.74 × 10-3 slug/ft³, u= 4.7 x 10-7 lb.s/ft²) Use moody chart (1) MIDAS Kel=0.3 Q3/Liquid ammonia at -20°C is flowing through a 30 m long section of a 5 mm diameter copper tube(e = 1.5 × 10-6 m) at a rate of 0.15 kg/s. Determine the pressure drop and the head losses. .μ= 2.36 × 10-4 kg/m.s)p = 665.1 kg/m³arrow_forward2/Y Y+1 2Cp Q1/ Show that Cda Az x P1 mactual Cdf Af R/T₁ 2pf(P1-P2-zxgxpf) Q2/ A simple jet carburetor has to supply 5 Kg of air per minute. The air is at a pressure of 1.013 bar and a temperature of 27 °C. Calculate the throat diameter of the choke for air flow velocity of 90 m/sec. Take velocity coefficient to be 0.8. Assume isentropic flow and the flow to be compressible. Quiz/ Determine the air-fuel ratio supplied at 5000 m altitude by a carburetor which is adjusted to give an air-fuel ratio of 14:1 at sea level where air temperature is 27 °C and pressure is 1.013 bar. The temperature of air decreases with altitude as given by the expression The air pressure decreases with altitude as per relation h = 19200 log10 (1.013), where P is in bar. State any assumptions made. t = ts P 0.0065harrow_forward36 2) Use the method of MEMBERS to determine the true magnitude and direction of the forces in members1 and 2 of the frame shown below in Fig 3.2. 300lbs/ft member-1 member-2 30° Fig 3.2. https://brightspace.cuny.edu/d21/le/content/433117/viewContent/29873977/Viewarrow_forward
- Can you solve this for me?arrow_forward5670 mm The apartment in the ground floor of three floors building in Fig. in Baghdad city. The details of walls, roof, windows and door are shown. The window is a double glazing and air space thickness is 1.3cm Poorly Fitted-with Storm Sash with wood strip and storm window of 0.6 cm glass thickness. The thickness of door is 2.5 cm. The door is Poor Installation. There are two peoples in each room. The height of room is 280 cm. assume the indoor design conditions are 25°C DBT and 50 RH, and moisture content of 8 gw/kga. The moisture content of outdoor is 10.5 gw/kga. Calculate heat gain for living room : الشقة في الطابق الأرضي من مبنى ثلاثة طوابق في مدينة بغداد يظهر في مخطط الشقة تفاصيل الجدران والسقف والنوافذ والباب. النافذة عبارة عن زجاج مزدوج وسمك الفراغ الهوائي 1.3 سم ضعيف الاحكام مع ساتر حماية مع إطار خشبي والنافذة بسماكة زجاج 0.6 سم سماكة الباب 2.5 سم. الباب هو تركيب ضعيف هناك شخصان في كل غرفة. ارتفاع الغرفة 280 سم. افترض أن ظروف التصميم الداخلي هي DBT25 و R50 ، ومحتوى الرطوبة 8…arrow_forwardHow do i solve this problem?arrow_forward
- Q4/ A compressor is driven motor by mean of a flat belt of thickness 10 mm and a width of 250 mm. The motor pulley is 300 mm diameter and run at 900 rpm and the compressor pulley is 1500 mm diameter. The shaft center distance is 1.5 m. The angle of contact of the smaller pulley is 220° and on the larger pulley is 270°. The coefficient of friction between the belt and the small pulley is 0.3, and between the belt and the large pulley is 0.25. The maximum allowable belt stress is 2 MPa and the belt density is 970 kg/m³. (a) What is the power capacity of the drive and (b) If the small pulley replaced by V-grooved pulley of diameter 300 mm, grooved angle of 34° and the coefficient of friction between belt and grooved pulley is 0.35. What will be the power capacity in this case, assuming that the diameter of the large pulley remain the same of 1500 mm.arrow_forwardYou are tasked with designing a power drive system to transmit power between a motor and a conveyor belt in a manufacturing facility as illustrated in figure. The design must ensure efficient power transmission, reliability, and safety. Given the following specifications and constraints, design drive system for this application: Specifications: Motor Power: The electric motor provides 10 kW of power at 1,500 RPM. Output Speed: The output shaft should rotate at 150 rpm. Design Decisions: Transmission ratio: Determine the necessary drive ratio for the system. Shaft Diameter: Design the shafts for both the motor and the conveyor end. Material Selection: Choose appropriate materials for the gears, shafts. Bearings: Select suitable rolling element bearings. Constraints: Space Limitation: The available space for the gear drive system is limited to a 1-meter-long section. Attribute 4 of CEP Depth of knowledge required Fundamentals-based, first principles analytical approach…arrow_forward- | العنوان In non-continuous dieless drawing process for copper tube as shown in Fig. (1), take the following data: Do-20mm, to=3mm, D=12mm, ti/to=0.6 and v.-15mm/s. Calculate: (1) area reduction RA, (2) drawing velocity v. Knowing that: ti: final thickness V. Fig. (1) ofthrearrow_forward
- A direct extrusion operation produces the cross section shown in Fig. (2) from an aluminum billet whose diameter 160 mm and length - 700 mm. Determine the length of the extruded section at the end of the operation if the die angle -14° 60 X Fig. (2) Note: all dimensions in mm.arrow_forwardFor hot rolling processes, show that the average strain rate can be given as: = (1+5)√RdIn(+1)arrow_forward: +0 usão العنوان on to A vertical true centrifugal casting process is used to produce bushings that are 250 mm long and 200 mm in outside diameter. If the rotational speed during solidification is 500 rev/min, determine the inside radii at the top and bottom of the bushing if R-2R. Take: -9.81 mis ۲/۱ ostrararrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Mechanical SPRING DESIGN Strategy and Restrictions in Under 15 Minutes!; Author: Less Boring Lectures;https://www.youtube.com/watch?v=dsWQrzfQt3s;License: Standard Youtube License