Chapter 12, Problem 92PP

If life exists elsewhere in our solar system, it may not have developed independently from life on Earth. Instead, it’s possible that microbes from Earth may have colonized other planets or moons by hitching a ride on a rock blasted from Earth’s surface by a meteor impact. If the impact gives the rock enough energy to escape into space (while at the same time not raising its temperature so high as to “cook” the microbes), the rock may eventually reach another body in the solar system. In fact, rocks from Mars are known to have reached Earth in just this way, although none are currently known to have contained microbes. Computer modeling can be used to estimate the probability that a rock ejected from the surface of the Earth with a speed greater than the escape speed will reach another planet. These computer models indicate that under the influence of gravitational fields from the other objects in the solar system, an ejected rock can take millions of years to travel from one planet to another. During this time any life “aboard” is continually exposed to the high radiation levels of space. Some researchers have calculated that a 3.0-m-diameter rock at a typical rock density of 3.0 g/cm³ is sufficient to shield some types of microbes from the hostile environment of space for several million years of travel.

The accompanying plot shows the residual speed of an ejected object—that is, the speed the object would have when infinitely far from the Earth—as a function of its speed at the surface of the Earth (its original ejection speed). By simulating the motion of rocks ejected from the Earth with a variety of speeds, researchers conclude that 0.03% of the rocks ejected such that they have a residual speed of 2.5 km/s will have reached Mars 2.0 million years later. Although this doesn’t seem like a high probability, there have been so many meteor impacts over the long history of the Earth that many ejected rocks must have reached Mars—though whether they carried microbes, and if they did, whether the microbes would have survived, are open questions.

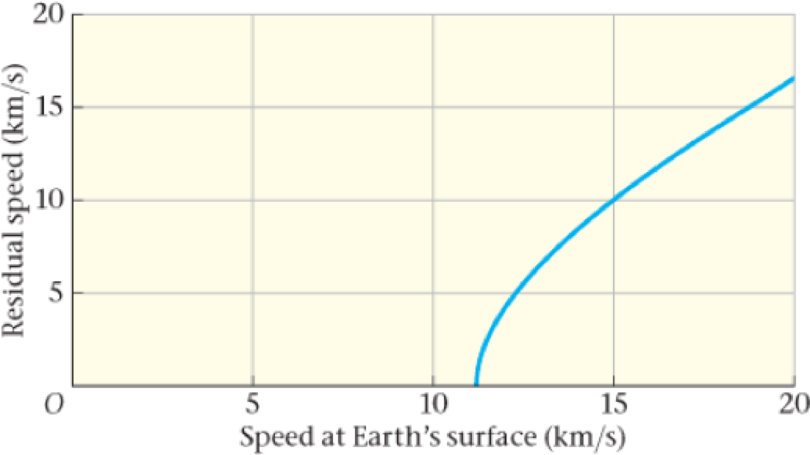
92. • What is the speed a rock needs to be given at the surface of the Earth in order for it to have a residual speed of 2.5 km/s?

1. A. 8.7 km/s
2. B. 10.9 km/s
3. C. 11.5 km/s
4. D. 13.7 km/s