Chapter 12, Problem 49P

(a)

To determine

Find the position of moving load to produce maximum moment.

Find the absolute maximum moment produced by the moving loads.

Find the maximum deflection produced by the load.

Answer to Problem 49P

The position of moving load to produce maximum moment is $\underset{\_}{18\text{ft}}$ when the maximum moment produced under wheel load 1.

The maximum moment is $\underset{\_}{405\text{ft-k}}$.

The maximum deflection is $\underset{\_}{\frac{107,587,492{\text{k-in}}^3}{EI}}$.

Explanation of Solution

Refer Table 2.3 “Live Load Impact Factor” in the text book.

Take the value of impact factor (I) for Cab-operated traveling crane support girders and their connections as 25%.

Find the increasing moving load using impact factor.

$\begin{array}{c}P=P_{\text{given}}+25\%\left(P_{\text{given}}\right)\\ =20+\left(25\%\right)\left(20\right)\\ =20+\frac{25}{100}\left(20\right)\\ =25\text{k}\end{array}$

Sketch the loading diagram as in Figure 1.

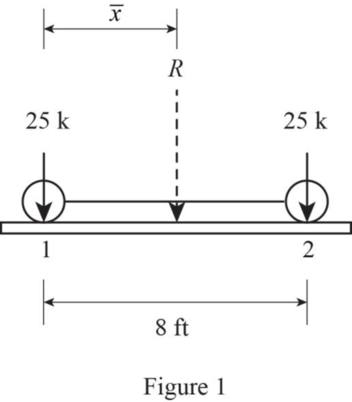
Refer Figure 1.

Find the resultant force.

$\begin{array}{c}R=25+25\\ =50\text{k}\end{array}$

Find the position of resultant using the equation.

$\begin{array}{c}\overline{x}=\frac{8}{2}\\ =4\text{ft}\end{array}$

Find the maximum moment.

The wheel loads are equal and so the moment produced under any one of the load.

Assume the maximum moment occurs under the wheel load 1. Therefore, the beam’s centerline divides the distance between the wheel load 1 and the resultant.

Draw the position of loading diagram as in Figure 2.

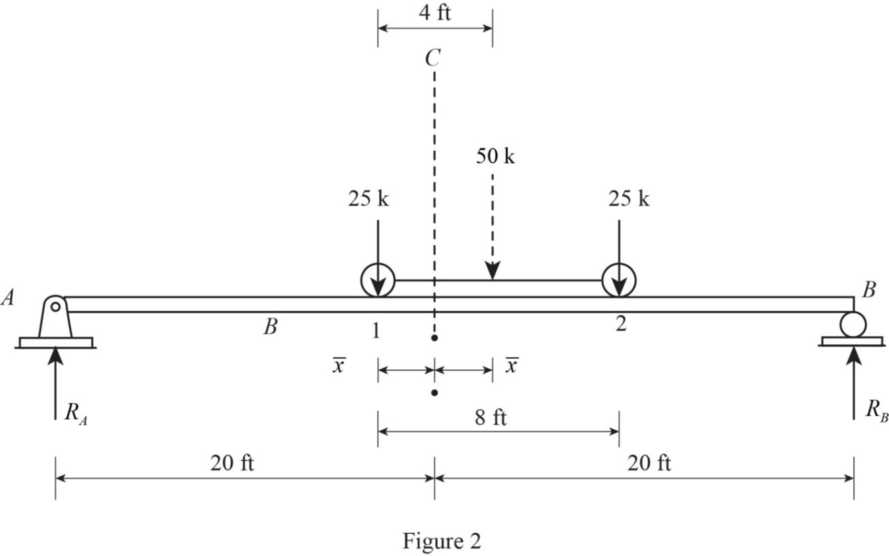
Refer Figure 2

Find the position of resultant from center of the beam.

$\begin{array}{c}\overline{x}=\frac{4}{2}\\ =2\text{ft}\end{array}$

Find the reaction at A.

Consider moment at B.

$\begin{array}{l}\Sigma M_B=0\\ R_A\left(40\right)-50\left(20-\overline{x}\right)=0\\ R_A\left(40\right)-50\left(20-2\right)=0\\ 40R_A=900\\ R_A=22.5\text{k}\end{array}$

Find the moment under wheel load 1.

Consider moment at wheel load 1.

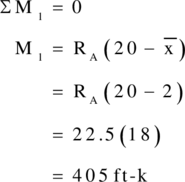
Find the moment under wheel load 2.

Consider moment at wheel load 2.

$\begin{array}{c}\Sigma M_2=0\\ M_2=R_A\left(20+6\right)-25\left(8\right)\\ =22.5\left(26\right)-200\\ =385\text{ft-k}\end{array}$

Therefore, the position of moving load to produce maximum moment is $\underset{\_}{18\text{ft}}$ when the maximum moment produced under wheel load 1.

Therefore, the maximum moment is $\underset{\_}{405\text{ft-k}}$ produced under wheel load 1

Draw the moment diagram using moment values at load 1 and 2 as in Figure 3.

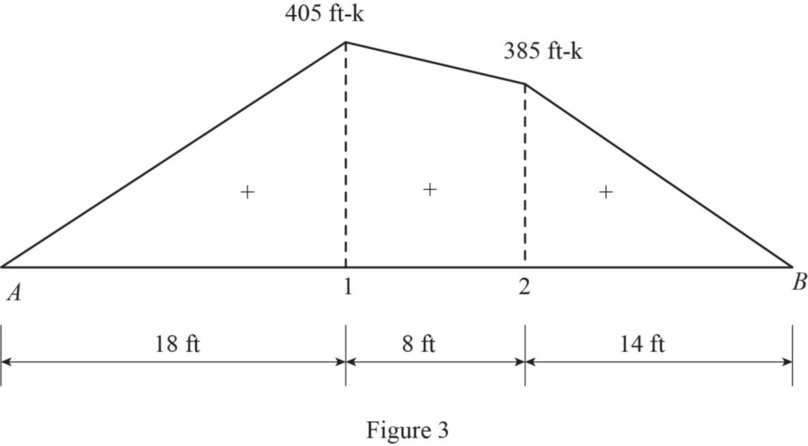
Assume maximum deflection occurs at M.

Draw the $\frac{M}{EI}$ diagram using Figure 3 as in Figure 4.

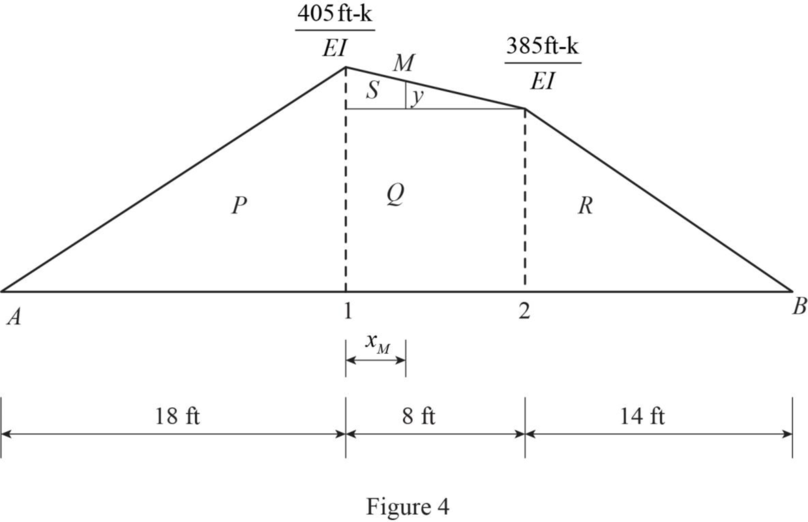
Refer Figure 4.

Find distance y using similar triangle.

$\begin{array}{l}\frac{y}{8-x_M}=\frac{405-385}{8}\\ \frac{y}{8-x_M}=2.5\\ y=20-2.5x_M\end{array}$

The maximum deflection occurs between point 1 and 2.

Find the deflection ${\Delta }_{DA}$.

$\begin{array}{c}{\Delta }_{DA}=\frac{1}{EI}\left[\begin{array}{l}\frac{1}{2}\left(14\right)\left(385\right)\left(\frac{2}{3}\times 14\right)+\left(8\right)\left(385\right)\left(14+4\right)\\ +\frac{1}{2}\left(8\right)\left(405-385\right)\left(14+\frac{2}{3}\times 8\right)+\frac{1}{2}\left(405\right)\left(18\right)\left(22+\frac{18}{3}\right)\end{array}\right]\\ =\frac{1}{EI}\left(25,153.33+55,440+1,546.67+102,060\right)\\ =\frac{184,200}{EI}\end{array}$

Find the slope at A.

$\begin{array}{c}{\theta }_A=\frac{\frac{184,200}{EI}}{L}\\ =\frac{184,200}{40\left(EI\right)}\\ =\frac{4,605}{EI}\end{array}$

Find the slope ${\theta }_{MA}$

$\begin{array}{c}{\theta }_{MA}=\frac{1}{EI}\left[\frac{1}{2}\left(18\right)\left(405\right)+\left(x_m\right)\left(385\right)+\left(\frac{20+y}{2}\right)\left(x_M\right)\right]\\ =\frac{1}{EI}\left[3,645+385x_M+\left(\frac{20+20-2.5x_M}{2}\right)\left(x_M\right)\right]\\ =\frac{1}{EI}\left[3,645+385x_M+\left(20+1.25x_M\right)\left(x_M\right)\right]\\ =\frac{1}{EI}\left[3,645+385x_M+20x_M+1.25x_M^2\right]\\ =\frac{1}{EI}\left(1.25x_M^2+405x_M+3,645\right)\end{array}$

Consider slope at M from A is equal to slope at A.

Find the point of maximum deflection $\left(x_M\right)$ from point 2.

$\begin{array}{l}{\theta }_{MA}={\theta }_A\\ 1.25x_M^2+405x_M+3,645=\frac{4,605}{EI}\\ 1.25x_M^2+405x_M-960=0\end{array}$        (1)

Solve Equation (1),

$\begin{array}{c}{x}_M=2.3533\text{ft}\\ \simeq 2.4\text{ft}\text{from right of wheel load 1}\end{array}$

Find the maximum deflection.

$\begin{array}{c}{\Delta }_{\max }={\Delta }_{AM}\\ =\frac{1}{EI}\left[\frac{1}{2}\left(405\right)\left(18\right)\left(\frac{2}{3}\times 18\right)+\left(x_M\right)\left(405\right)\left(18+\frac{x_M}{2}\right)-\frac{1}{2}\left(\frac{20}{8}{x}_M\right)\left(x_M\right)\left(18+\frac{2}{3}\times x_M\right)\right]\\ =\frac{1}{EI}\left[43,740+7,290x_M+202.5x_M^2-\frac{1}{2}\left(2.5x_M\right)\left(x_M\right)\left(18+\frac{2}{3}{x}_M\right)\right]\\ =\frac{1}{EI}\left[43,740+7,290\left(2.4\right)+202.5{\left(2.4\right)}^2-\frac{1}{2}\left(2.5\times 2.4\right)\left(2.4\right)\left(18+\frac{2}{3}\times 2.4\right)\right]\\ =\frac{1}{EI}\left[43,740+17,496+1,166.4-141.12\right]\\ =\frac{62,261.28{\text{k-ft}}^3}{EI}\\ =\frac{62,261.28\times {\left(12\right)}^3{\text{k-in}}^3}{EI}\\ \simeq \frac{107,587,492{\text{k-in}}^3}{EI}\end{array}$

Therefore, the maximum deflection is $\underset{\_}{\frac{107,587,492{\text{k-in}}^3}{EI}}$.

(b)

To determine

Find the maximum moment and maximum deflection when the moving load placed symmetrically.

Compare the deflections of both part.

Answer to Problem 49P

The maximum moment is $\underset{\_}{400\text{ft-k}}$

The maximum deflection at center of the beam is $\underset{\_}{\frac{108,749,000{\text{k-in}}^3}{EI}}$

Explanation of Solution

Find the maximum moment.

Place the moving load symmetrically.

Draw the position of loading diagram as in Figure 5.

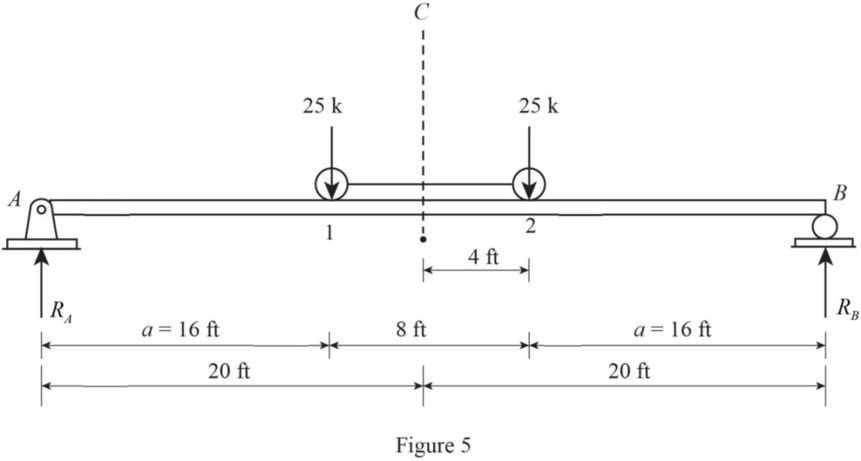
Refer Figure 5.

Find the reaction at A and B.

The loading are symmetrical.

$\begin{array}{c}{R}_A=R_B=\frac{25+25}{2}\\ =25\text{k}\end{array}$

Find the moment under wheel load 1.

Consider moment at wheel load 1 and 2.

$\begin{array}{c}\Sigma M_1=0\\ M_1=M_2\\ =R_A\left(20-4\right)\\ =25\left(16\right)\\ =400\text{ft-k}\end{array}$

Therefore, the maximum moment is $\underset{\_}{400\text{ft-k}}$.

Draw the moment diagram using the calculated values as in Figure 6.

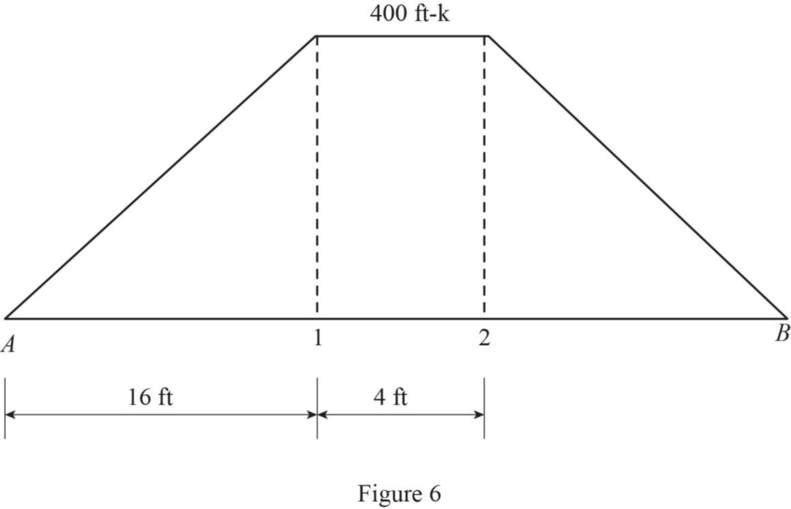
Refer Figure 6.

The maximum deflection occurs at center for symmetrical loading of simply supported beam.

Find the maximum deflection.

$\begin{array}{c}{\Delta }_{\max }={\Delta }_{AM}\\ =\frac{1}{EI}\left[\frac{1}{2}\left(16\right)\left(400\right)\left(\frac{2}{3}\times 16\right)+\left(400\right)\left(4\right)\left(16+2\right)\right]\\ =\frac{1}{EI}\left[34,133.33+28,800\right]\\ =\frac{62,933.333{\text{k-ft}}^3}{EI}\\ =\frac{62,933.333\times {\left(12\right)}^3{\text{k-in}}^3}{EI}\\ \simeq \frac{108,749,000{\text{k-in}}^3}{EI}\end{array}$

Therefore, the maximum deflection at center of the beam is $\underset{\_}{\frac{108,749,000{\text{k-in}}^3}{EI}}$.

Comparison of deflection for both part (a) and (b):

Maximum deflection occurs when loads are centered symmetrically on the beam span.