Single Variable Calculus: Concepts and Contexts, Enhanced Edition

4th Edition

ISBN: 9781337687805

Author: James Stewart

Publisher: Cengage Learning

See similar textbooks

Concept explainers

Exponential Growth Model

The relation that represents an exponential function is:

Videos

Question

Chapter 1.1, Problem 9E

(a)

To determine

To estimate: The global average temperature in the year 1950.

(a)

Expert Solution

Answer to Problem 9E

The global average temperature in 1950 is 13.8°C.

Explanation of Solution

During the 20th century, the global average temperature in the graph, the x-axis represents the period (t) between 1900 and 2000, and the y-axis represents the global average temperature (T) in degree Celsius.

Draw the vertical line from the year 1950 to meet the graph of global average temperature during the 20th century. And then, draw the horizontal line towards the y-axis as shown below in Figure 1.

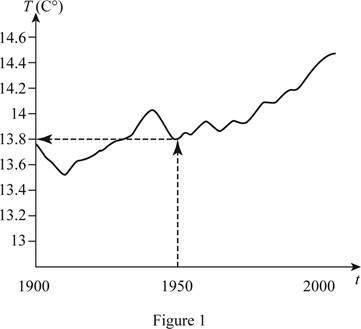
Single Variable Calculus: Concepts and Contexts, Enhanced Edition, Chapter 1.1, Problem 9E , additional homework tip 1

From Figure 1, it is found that the temperature in 1950 is below 14°C and approximate to 13.8°C. Therefore, the temperature was about13.8°C.

(b)

To determine

To estimate: The year when the average temperature was 14.2°C.

(b)

Expert Solution

Answer to Problem 9E

The average temperature was nearly 14.2°C in the year 1990.

Explanation of Solution

Draw the horizontal line from 14.2°C to meet the graph of global average temperature during the 20th century. And then, draw the vertical line until it meets the x-axis, which is shown below in Figure 2.

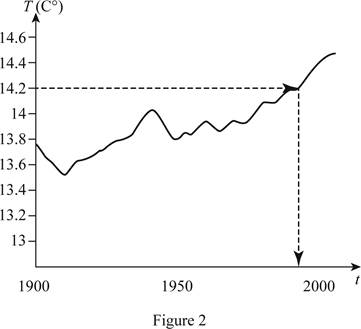
Single Variable Calculus: Concepts and Contexts, Enhanced Edition, Chapter 1.1, Problem 9E , additional homework tip 2

From Figure 2, it is found that the average temperature was 14.2°C in the year 1990.

(c)

To determine

To estimate: The year in which the temperature was too high and too low.

(c)

Expert Solution

Answer to Problem 9E

The temperature was too low in the year 1910 and it was too high in the year 2005.

Explanation of Solution

The graph of the global average temperature during the 20th century follows the cyclic pattern with highs and lows. Draw the vertical lines from the lowest temperature to the highest temperature towards x-axis as shown below in Figure 3.

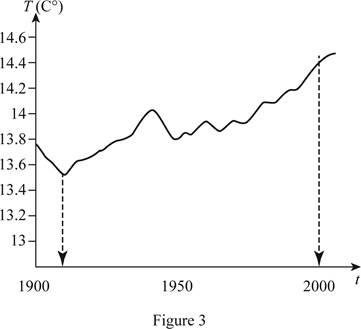
Single Variable Calculus: Concepts and Contexts, Enhanced Edition, Chapter 1.1, Problem 9E , additional homework tip 3

From Figure 3, it is noticeable that the temperature was the lowest around 13.5°C over the year 1910. Thus, the temperature was lowest in the year 1910.

From Figure 3, it is noticeable that the temperature was the mostly around 14.4°C over the year 2005. Thus, the temperature was the highest around the year 2005.

(d)

To determine

To estimate: The range of T.

(d)

Expert Solution

Answer to Problem 9E

The range of T is 13.5≤T≤14.5 .

Explanation of Solution

The range of a function is the set of all possible y values of the graph. Thus, the range of the function is 13.5≤T≤14.5 .

Chapter 1.1, Problem 8E

Chapter 1.1, Problem 10E

Chapter 1 Solutions

Single Variable Calculus: Concepts and Contexts, Enhanced Edition

Ch. 1.1 - The graph of a function f is given. (a) State the...Ch. 1.1 - The graphs of f and g are given. (a) State the...Ch. 1.1 - Figure 1 was recorded by an instrument operated by...Ch. 1.1 - Prob. 5E Ch. 1.1 - Determine whether the curve is the graph of a...Ch. 1.1 - Prob. 7E Ch. 1.1 - Prob. 8E Ch. 1.1 - Prob. 9E Ch. 1.1 - Prob. 10E Ch. 1.1 - Prob. 11E

Ch. 1.1 - Prob. 12E Ch. 1.1 - The graph shows the power consumption for a day in...Ch. 1.1 - Prob. 14E Ch. 1.1 - Prob. 15E Ch. 1.1 - Prob. 16E Ch. 1.1 - Sketch the graph of the amount of a particular...Ch. 1.1 - You place a frozen pie in an oven and bake it for...Ch. 1.1 - Prob. 19E Ch. 1.1 - Prob. 20E Ch. 1.1 - Prob. 21E Ch. 1.1 - Prob. 22E Ch. 1.1 - Prob. 23E Ch. 1.1 - Prob. 24E Ch. 1.1 - Prob. 25E Ch. 1.1 - Prob. 26E Ch. 1.1 - Prob. 27E Ch. 1.1 - Prob. 28E Ch. 1.1 - Prob. 29E Ch. 1.1 - Prob. 30E Ch. 1.1 - Prob. 31E Ch. 1.1 - Prob. 32E Ch. 1.1 - Prob. 33E Ch. 1.1 - Prob. 34E Ch. 1.1 - Prob. 35E Ch. 1.1 - Prob. 36E Ch. 1.1 - Prob. 37E Ch. 1.1 - Prob. 38E Ch. 1.1 - Prob. 39E Ch. 1.1 - Prob. 40E Ch. 1.1 - Prob. 41E Ch. 1.1 - Prob. 42E Ch. 1.1 - Prob. 43E Ch. 1.1 - Prob. 44E Ch. 1.1 - Prob. 45E Ch. 1.1 - Prob. 46E Ch. 1.1 - Prob. 47E Ch. 1.1 - Prob. 48E Ch. 1.1 - Find an expression for the function whose graph is...Ch. 1.1 - Prob. 50E Ch. 1.1 - Prob. 51E Ch. 1.1 - Prob. 52E Ch. 1.1 - Prob. 53E Ch. 1.1 - Prob. 54E Ch. 1.1 - Prob. 55E Ch. 1.1 - Prob. 56E Ch. 1.1 - Prob. 57E Ch. 1.1 - A Norman window has the shape of a rectangle...Ch. 1.1 - Prob. 59E Ch. 1.1 - Prob. 60E Ch. 1.1 - Prob. 61E Ch. 1.1 - Prob. 62E Ch. 1.1 - Prob. 63E Ch. 1.1 - Prob. 64E Ch. 1.1 - Prob. 65E Ch. 1.1 - Prob. 66E Ch. 1.1 - Prob. 67E Ch. 1.1 - Prob. 68E Ch. 1.1 - Prob. 69E Ch. 1.1 - Prob. 70E Ch. 1.1 - Prob. 71E Ch. 1.1 - Prob. 72E Ch. 1.1 - Prob. 73E Ch. 1.1 - Prob. 74E Ch. 1.2 - Classify each function as a power function, root...Ch. 1.2 - Prob. 2E Ch. 1.2 - Prob. 3E Ch. 1.2 - Prob. 4E Ch. 1.2 - Prob. 5E Ch. 1.2 - Prob. 6E Ch. 1.2 - Prob. 7E Ch. 1.2 - Prob. 8E Ch. 1.2 - Prob. 9E Ch. 1.2 - Prob. 10E Ch. 1.2 - Prob. 11E Ch. 1.2 - The manager of a weekend flea market knows from...Ch. 1.2 - Prob. 13E Ch. 1.2 - Prob. 14E Ch. 1.2 - Biologists have noticed that the chirping rate of...Ch. 1.2 - Prob. 16E Ch. 1.2 - Prob. 17E Ch. 1.2 - Prob. 18E Ch. 1.2 - Prob. 19E Ch. 1.2 - Prob. 20E Ch. 1.2 - Prob. 21E Ch. 1.2 - Prob. 22E Ch. 1.2 - Prob. 23E Ch. 1.2 - Prob. 24E Ch. 1.2 - Prob. 25E Ch. 1.2 - Prob. 26E Ch. 1.3 - Suppose the graph of f is given. Write equations...Ch. 1.3 - Prob. 2E Ch. 1.3 - The graph of y=f(x) is given. Match each equation...Ch. 1.3 - Prob. 4E Ch. 1.3 - Prob. 5E Ch. 1.3 - Prob. 6E Ch. 1.3 - Prob. 7E Ch. 1.3 - Prob. 8E Ch. 1.3 - Prob. 9E Ch. 1.3 - Prob. 10E Ch. 1.3 - Prob. 11E Ch. 1.3 - Prob. 12E Ch. 1.3 - Prob. 13E Ch. 1.3 - Prob. 14E Ch. 1.3 - Prob. 15E Ch. 1.3 - Prob. 16E Ch. 1.3 - Prob. 17E Ch. 1.3 - Prob. 18E Ch. 1.3 - Prob. 19E Ch. 1.3 - Prob. 20E Ch. 1.3 - Prob. 21E Ch. 1.3 - Prob. 22E Ch. 1.3 - Prob. 23E Ch. 1.3 - Prob. 24E Ch. 1.3 - The city of New Orleans is located at latitude...Ch. 1.3 - Prob. 26E Ch. 1.3 - Prob. 27E Ch. 1.3 - Prob. 28E Ch. 1.3 - Prob. 29E Ch. 1.3 - Prob. 30E Ch. 1.3 - Prob. 31E Ch. 1.3 - Prob. 32E Ch. 1.3 - Prob. 33E Ch. 1.3 - Prob. 34E Ch. 1.3 - Prob. 35E Ch. 1.3 - Prob. 36E Ch. 1.3 - Prob. 37E Ch. 1.3 - Prob. 38E Ch. 1.3 - Prob. 39E Ch. 1.3 - Prob. 40E Ch. 1.3 - Prob. 41E Ch. 1.3 - Prob. 42E Ch. 1.3 - Prob. 43E Ch. 1.3 - Prob. 44E Ch. 1.3 - Express the function in the form f g. 47. v(t) =...Ch. 1.3 - Prob. 46E Ch. 1.3 - Prob. 47E Ch. 1.3 - Prob. 48E Ch. 1.3 - Prob. 49E Ch. 1.3 - Prob. 50E Ch. 1.3 - Prob. 51E Ch. 1.3 - Use the given graphs of f and g to estimate the...Ch. 1.3 - Prob. 53E Ch. 1.3 - Prob. 54E Ch. 1.3 - A ship is at a speed of 30km/h parallel to a...Ch. 1.3 - Prob. 56E Ch. 1.3 - Prob. 57E Ch. 1.3 - The Heaviside function defined in Exercise 59 can...Ch. 1.3 - Prob. 59E Ch. 1.3 - Prob. 60E Ch. 1.3 - Prob. 61E Ch. 1.3 - Prob. 62E Ch. 1.3 - Prob. 63E Ch. 1.3 - Prob. 64E Ch. 1.4 - Prob. 1E Ch. 1.4 - Prob. 2E Ch. 1.4 - Prob. 3E Ch. 1.4 - Prob. 4E Ch. 1.4 - Prob. 5E Ch. 1.4 - Prob. 6E Ch. 1.4 - Prob. 7E Ch. 1.4 - Prob. 8E Ch. 1.4 - Prob. 9E Ch. 1.4 - Prob. 10E Ch. 1.4 - Prob. 11E Ch. 1.4 - Prob. 12E Ch. 1.4 - Prob. 13E Ch. 1.4 - Prob. 14E Ch. 1.4 - Prob. 15E Ch. 1.4 - Prob. 16E Ch. 1.4 - Prob. 17E Ch. 1.4 - Prob. 18E Ch. 1.4 - Prob. 19E Ch. 1.4 - Prob. 20E Ch. 1.4 - Prob. 21E Ch. 1.4 - Prob. 22E Ch. 1.4 - Prob. 23E Ch. 1.4 - Prob. 24E Ch. 1.4 - Prob. 25E Ch. 1.4 - Prob. 26E Ch. 1.4 - Prob. 27E Ch. 1.4 - Prob. 28E Ch. 1.4 - Prob. 29E Ch. 1.4 - Prob. 30E Ch. 1.4 - Prob. 31E Ch. 1.4 - Prob. 32E Ch. 1.4 - Prob. 33E Ch. 1.4 - Prob. 34E Ch. 1.4 - Prob. 35E Ch. 1.4 - Prob. 36E Ch. 1.4 - Prob. 37E Ch. 1.4 - Prob. 38E Ch. 1.5 - Use the Law of Exponents to rewrite and simplify...Ch. 1.5 - Use the Law of Exponents to rewrite and simplify...Ch. 1.5 - Prob. 3E Ch. 1.5 - Use the Law of Exponents to rewrite and simplify...Ch. 1.5 - Prob. 5E Ch. 1.5 - Prob. 6E Ch. 1.5 - Prob. 7E Ch. 1.5 - Prob. 8E Ch. 1.5 - Prob. 9E Ch. 1.5 - Prob. 10E Ch. 1.5 - Prob. 11E Ch. 1.5 - Prob. 12E Ch. 1.5 - Prob. 13E Ch. 1.5 - Prob. 14E Ch. 1.5 - Make a rough sketch of the graph of the function....Ch. 1.5 - Prob. 16E Ch. 1.5 - Prob. 17E Ch. 1.5 - Prob. 18E Ch. 1.5 - Prob. 19E Ch. 1.5 - Prob. 20E Ch. 1.5 - Prob. 21E Ch. 1.5 - Find the exponential function f(x) = Cbx whose...Ch. 1.5 - Prob. 23E Ch. 1.5 - Suppose you are offered a job that lasts one...Ch. 1.5 - Prob. 25E Ch. 1.5 - Prob. 26E Ch. 1.5 - Prob. 27E Ch. 1.5 - Prob. 28E Ch. 1.5 - Prob. 29E Ch. 1.5 - A bacteria culture starts with 500 bacteria and...Ch. 1.5 - The half-life of bismuth-210, 210Bi, is 5 days....Ch. 1.5 - Prob. 32E Ch. 1.5 - Prob. 33E Ch. 1.5 - Prob. 34E Ch. 1.5 - Prob. 35E Ch. 1.5 - Prob. 36E Ch. 1.6 - (a) What is a one-to-one function? (b) How can you...Ch. 1.6 - Prob. 2E Ch. 1.6 - Prob. 3E Ch. 1.6 - Prob. 4E Ch. 1.6 - A function is given by a table of values, a graph,...Ch. 1.6 - A function is given by a table of values, a graph,...Ch. 1.6 - Prob. 7E Ch. 1.6 - A function is given by a table of values, a graph,...Ch. 1.6 - Prob. 9E Ch. 1.6 - Prob. 10E Ch. 1.6 - Prob. 11E Ch. 1.6 - Prob. 12E Ch. 1.6 - Prob. 13E Ch. 1.6 - Prob. 14E Ch. 1.6 - Assume that f is a one-to-one function. (a) If...Ch. 1.6 - Prob. 16E Ch. 1.6 - Prob. 17E Ch. 1.6 - Prob. 18E Ch. 1.6 - Prob. 19E Ch. 1.6 - Prob. 20E Ch. 1.6 - Prob. 21E Ch. 1.6 - Prob. 22E Ch. 1.6 - Prob. 23E Ch. 1.6 - Prob. 24E Ch. 1.6 - Find a formula for the inverse of the function....Ch. 1.6 - Prob. 26E Ch. 1.6 - Prob. 27E Ch. 1.6 - Prob. 28E Ch. 1.6 - Prob. 29E Ch. 1.6 - Prob. 30E Ch. 1.6 - Prob. 31E Ch. 1.6 - Prob. 32E Ch. 1.6 - Prob. 33E Ch. 1.6 - Prob. 34E Ch. 1.6 - Prob. 35E Ch. 1.6 - Prob. 36E Ch. 1.6 - Prob. 37E Ch. 1.6 - Prob. 38E Ch. 1.6 - Prob. 39E Ch. 1.6 - Prob. 40E Ch. 1.6 - Prob. 41E Ch. 1.6 - Use Formula 10 to evaluate each logarithm correct...Ch. 1.6 - Prob. 43E Ch. 1.6 - Prob. 44E Ch. 1.6 - Prob. 45E Ch. 1.6 - Prob. 46E Ch. 1.6 - Prob. 47E Ch. 1.6 - Make a rough sketch of the graph of each function....Ch. 1.6 - Solve each equation for x. 51. (a) e74x=6 (b)...Ch. 1.6 - Prob. 50E Ch. 1.6 - Prob. 51E Ch. 1.6 - Prob. 52E Ch. 1.6 - Prob. 53E Ch. 1.6 - Prob. 54E Ch. 1.6 - Prob. 55E Ch. 1.6 - Prob. 56E Ch. 1.6 - Prob. 57E Ch. 1.6 - Prob. 58E Ch. 1.6 - Prob. 59E Ch. 1.6 - Prob. 60E Ch. 1.6 - Prob. 61E Ch. 1.6 - Prob. 62E Ch. 1.7 - Prob. 1E Ch. 1.7 - Prob. 2E Ch. 1.7 - Prob. 3E Ch. 1.7 - Prob. 4E Ch. 1.7 - Prob. 5E Ch. 1.7 - Prob. 6E Ch. 1.7 - Prob. 7E Ch. 1.7 - Prob. 8E Ch. 1.7 - Prob. 9E Ch. 1.7 - Prob. 10E Ch. 1.7 - Prob. 11E Ch. 1.7 - Prob. 12E Ch. 1.7 - Prob. 13E Ch. 1.7 - Prob. 14E Ch. 1.7 - Prob. 15E Ch. 1.7 - Prob. 16E Ch. 1.7 - Prob. 17E Ch. 1.7 - Prob. 18E Ch. 1.7 - Prob. 19E Ch. 1.7 - Prob. 20E Ch. 1.7 - Prob. 21E Ch. 1.7 - Prob. 22E Ch. 1.7 - Prob. 23E Ch. 1.7 - Prob. 24E Ch. 1.7 - Prob. 25E Ch. 1.7 - Prob. 26E Ch. 1.7 - Prob. 27E Ch. 1.7 - Prob. 28E Ch. 1.7 - Prob. 29E Ch. 1.7 - Prob. 30E Ch. 1.7 - Prob. 31E Ch. 1.7 - Prob. 32E Ch. 1.7 - Prob. 33E Ch. 1.7 - Prob. 34E Ch. 1.7 - Prob. 35E Ch. 1.7 - Prob. 36E Ch. 1.7 - Prob. 37E Ch. 1.7 - Prob. 38E Ch. 1.7 - Prob. 39E Ch. 1.7 - Prob. 40E Ch. 1.7 - Prob. 41E Ch. 1.7 - Prob. 42E Ch. 1.7 - Prob. 43E Ch. 1.7 - Prob. 44E Ch. 1.7 - Prob. 45E Ch. 1.7 - Prob. 46E Ch. 1 - Prob. 1RQ Ch. 1 - Prob. 2RQ Ch. 1 - Prob. 3RQ Ch. 1 - Prob. 4RQ Ch. 1 - Prob. 5RQ Ch. 1 - Prob. 6RQ Ch. 1 - Prob. 7RQ Ch. 1 - Determine whether the statement is true or false....Ch. 1 - Determine whether the statement is true or false....Ch. 1 - Prob. 10RQ Ch. 1 - Prob. 11RQ Ch. 1 - Prob. 12RQ Ch. 1 - (a) What is a function? What are its domain and...Ch. 1 - Discuss four ways of representing a function....Ch. 1 - (a) What is an even function? How can you tell if...Ch. 1 - Prob. 4RCC Ch. 1 - Prob. 5RCC Ch. 1 - Prob. 6RCC Ch. 1 - Prob. 7RCC Ch. 1 - Prob. 8RCC Ch. 1 - Suppose that f has domain A and g has domain B....Ch. 1 - Prob. 10RCC Ch. 1 - Prob. 11RCC Ch. 1 - Prob. 12RCC Ch. 1 - Prob. 13RCC Ch. 1 - Let f be the function whose graph is given. (a)...Ch. 1 - Prob. 2RE Ch. 1 - Prob. 3RE Ch. 1 - Prob. 4RE Ch. 1 - Prob. 5RE Ch. 1 - Prob. 6RE Ch. 1 - Prob. 7RE Ch. 1 - Prob. 8RE Ch. 1 - Suppose that the graph of .f is given. Describe...Ch. 1 - Prob. 10RE Ch. 1 - Prob. 11RE Ch. 1 - Prob. 12RE Ch. 1 - Prob. 13RE Ch. 1 - Prob. 14RE Ch. 1 - Prob. 15RE Ch. 1 - Prob. 16RE Ch. 1 - Prob. 17RE Ch. 1 - Prob. 18RE Ch. 1 - Prob. 19RE Ch. 1 - Prob. 20RE Ch. 1 - Prob. 22RE Ch. 1 - Prob. 23RE Ch. 1 - Prob. 24RE Ch. 1 - Prob. 25RE Ch. 1 - Prob. 26RE Ch. 1 - The half-life of palladium-100, 100Pd, is four...Ch. 1 - The population of a certain species in a limited...Ch. 1 - Prob. 29RE Ch. 1 - Prob. 30RE Ch. 1 - Prob. 31RE Ch. 1 - Prob. 32RE Ch. 1 - Prob. 33RE Ch. 1 - Prob. 34RE Ch. 1 - One of the legs of a right triangle has length 4...Ch. 1 - Prob. 2P Ch. 1 - Prob. 3P Ch. 1 - Prob. 4P Ch. 1 - Prob. 5P Ch. 1 - Prob. 6P Ch. 1 - Prob. 7P Ch. 1 - Prob. 8P Ch. 1 - Prob. 9P Ch. 1 - Prob. 10P Ch. 1 - Prob. 11P Ch. 1 - Prob. 12P Ch. 1 - Prob. 13P Ch. 1 - Prob. 14P Ch. 1 - Prob. 15P Ch. 1 - Prob. 16P Ch. 1 - Prob. 17P Ch. 1 - Prove that 1 + 3 + 5 + + (2n l ) = n2.Ch. 1 - Prob. 19P Ch. 1 - Prob. 20P

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.