Chapter 1.1, Problem 20E

(a)

To determine

To sketch: The rough graph of the horizontal distance traveled $x\left(t\right)$ by an airplane.

Explanation of Solution

It is given that $x\left(t\right)$ denotes the horizontal distance traveled. Also, the airplane travels 400 miles in an hour. So, when the time increases, the number of miles traveled by the airplane increases. Therefore, the rough graph of $x\left(t\right)$ is shown below in Figure 1.

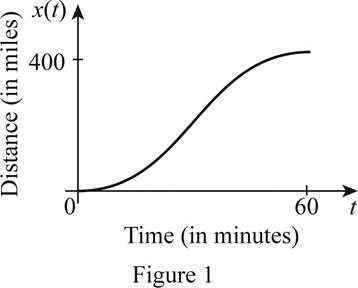
In Figure 1, the increasing curve represents the distance traveled by the airplane in one hour.

(b)

To determine

To sketch: The rough graph of the altitude of the plane, $y\left(t\right)$.

Explanation of Solution

It is given that $y\left(t\right)$ denotes the altitude of the plane. As the speed of the airplane is slow during takeoff and landing time, the altitude of the airplane will be less during takeoff and landing when compared with the altitude during the middle of the journey. Therefore, the rough graph of $y\left(t\right)$ is shown below in Figure 2.

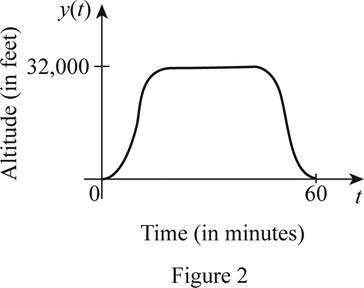
From Figure 2, it is observed that there is a variation in the altitude of the airplane during takeoff and landing time.

(c)

To determine

To sketch: A rough graph of the ground speed.

Explanation of Solution

Ground speed is the relative speed of the airplane to the ground. Generally, the ground speed of the airplane will be slow at the time of take off. Then, the speed will be increased and remains constant after a few minutes of take off. Again, at the time of landing, the ground speed of the airplane will be slow. So, at the initial and landing stage, the speed of the airplane will be slow. The rough graph of ground speed is shown below in Figure 3.

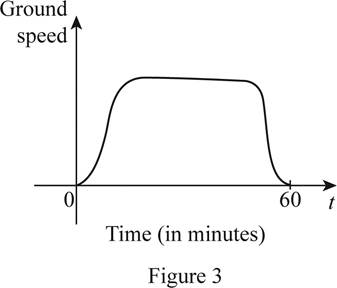
It is observed from Figure 3 that there is a variation in the ground speed of the airplane during the takeoff and landing time.

(d)

To determine

To sketch: A possible graph of the vertical velocity.

Explanation of Solution

The vertical velocity is either positive or negative, as it a vector quantity. As the airplane moves upward during takeoff, the vertical velocity is positive and as the airplane moves downward during landing, the vertical velocity is negative. Also, the airplane travels in a constant speed during the middle part of the journey with the vertical velocity as zero. The rough sketch of the vertical velocity is shown below in Figure 4.

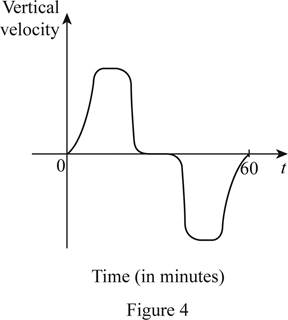
From Figure 4, it is observed that the upper part of the graph is the same as the lower part.