Chapter 1.1, Problem 80E

Taxicab fares. In New York City, taxicabs change passengers $2.50 for entering a cab and then $050 for each one-fifth of a mile (or fraction thereof) traveled. (There are additional charge for slow traffic and idle times, but these are not considered in this problem.) If x presents the distance traveled in miles, then $C\left(x\right)$ is the cost of the taxi fare, where

$\begin{array}{l}C\left(x\right)=\$2.50,\text{if}x=0,\\ C\left(x\right)=\$3.00,\text{if}0<x\le 0.2,\\ C\left(x\right)=\$3.50,\text{if}0.2<x\le 0.4,\\ C\left(x\right)=\$4.00,\text{if}0.4<x\le 0.6,\end{array}$

and so on. The graph of C is show below. (Source; New York City Taxi and Limousine Commission.)

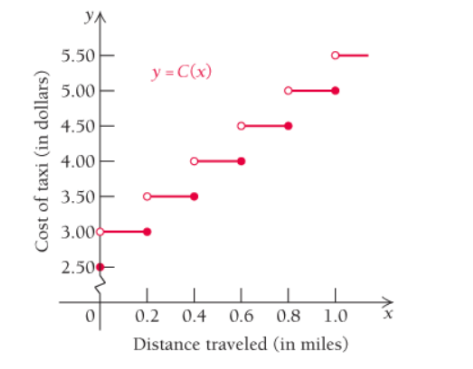
Using the graph of the taxicab fare function, find each of the following limits. if it exists.

$\underset{x\to {0.2}^{-}}{\lim }C\left(x\right),\underset{x\to {0.2}^{+}}{\lim }C\left(x\right),\underset{x\to 0.2}{\lim }C\left(x\right)$