
CALCULUS+ITS...,EXP.(LL)-W/CODE NVCC
19th Edition
ISBN: 9780136572671
Author: BITTINGER
Publisher: PEARSON C
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 1.1, Problem 30E
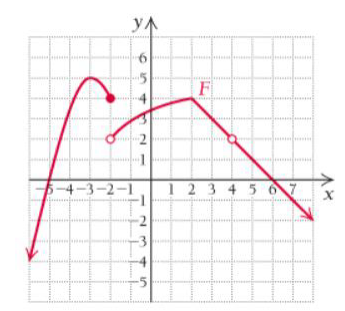
For Exercises 15–22, use the following graph of F to find each limit. When necessary, state that the limit does not exist.
Expert Solution & Answer
Trending nowThis is a popular solution!

Students have asked these similar questions
い
ined sove in beaper
Anting.
Pu+965
na lake
an accident and lands at the bottom of the lake
Q2// Find the volume of the region in first octant bounded by the coordinate
planes and the plane passing through (1, 0, 0), (0, 2, 0), and (0, 0, 3).
Q/Evaluate({ } } 3xze* dydzdx.
|
Evaluate (3xze** dydzdx.
ined sove in peaper
+9198
PU+965
Lake
Find the volume of th solid bounded above by the Cy
2=6-1
o the sides by the cylinder x+y=9, and below by the xy-plane
...
+①
العنوان
>
पर
ined sove in peaper
ང་
PU+965
Q2// Draw and Evaluate, or Integrate, the function f(u, v)
= (1+u2+v²)3
over the region enclosed by one loop of the lemniscate (u² + v²)² -
(u² + v²) = 0.
Lake
2 4-2² y
7357
r
QI// Evaluate f²² cos(y) dxdydz.
4-y
이
Chapter 1 Solutions
CALCULUS+ITS...,EXP.(LL)-W/CODE NVCC
Ch. 1.1 - Complete each of the following statements.
1. As x...Ch. 1.1 - Complete each of the following statements. As x...Ch. 1.1 - Complete each of the following statements.
7. The...Ch. 1.1 - Complete each of the following statements. The...Ch. 1.1 - Complete each of the following statements. The...Ch. 1.1 - Complete each of the following statements. The...Ch. 1.1 - Complete each of the following statements.
4. The...Ch. 1.1 - Complete each of the following statements. The...Ch. 1.1 - Complete each of the following statements.
6. The...Ch. 1.1 - For Exercises 11 and 12, consider the function f...
Ch. 1.1 - For Exercises 11 and 12, consider the function f...Ch. 1.1 - For Exercises 13 and 14, consider the function g...Ch. 1.1 - For Exercises 13 and 14, consider the function g...Ch. 1.1 - For Exercises 15–22, use the following graph of F...Ch. 1.1 - For Exercises 25-32, use the following graph of F...Ch. 1.1 - For Exercises 15–22, use the following graph of F...Ch. 1.1 - For Exercises 15–22, use the following graph of F...Ch. 1.1 - For Exercises 15–22, use the following graph of F...Ch. 1.1 - For Exercises 1522, use the following graph of F...Ch. 1.1 - For Exercises 25-32, use the following graph of F...Ch. 1.1 - For Exercises 1522, use the following graph of F...Ch. 1.1 - For Exercises 23-30, use the following graph of G...Ch. 1.1 - For Exercises 23-30, use the following graph of G...Ch. 1.1 - For Exercises 23-30, use the following graph of G...Ch. 1.1 - For Exercises 23-30, use the following graph of G...Ch. 1.1 - For Exercises 23-30, use the following graph of G...Ch. 1.1 - For Exercises 23-30, use the following graph of G...Ch. 1.1 - For Exercises 23-30, use the following graph of G...Ch. 1.1 - For Exercises 23-30, use the following graph of G...Ch. 1.1 - For Exercises 3140, use the following graph of H...Ch. 1.1 - For Exercises 31–40, use the following graph of H...Ch. 1.1 - For Exercises 3140, use the following graph of H...Ch. 1.1 - For Exercises 3140, use the following graph of H...Ch. 1.1 - For Exercises 31–40, use the following graph of H...Ch. 1.1 - For Exercises 3140, use the following graph of H...Ch. 1.1 - For Exercises 31–40, use the following graph of H...Ch. 1.1 - For Exercises 3140, use the following graph of H...Ch. 1.1 - For Exercises 3140, use the following graph of H...Ch. 1.1 - For Exercises 31–40, use the following graph of H...Ch. 1.1 - For Exercises 41-50, use the following graph of f...Ch. 1.1 - For Exercises 41-50, use the following graph of f...Ch. 1.1 - For Exercises 41-50, use the following graph of f...Ch. 1.1 - For Exercises 41-50, use the following graph of f...Ch. 1.1 - For Exercises 41-50, use the following graph of f...Ch. 1.1 - For Exercises 41-50, use the following graph of f...Ch. 1.1 - For Exercises 41-50, use the following graph of f...Ch. 1.1 - For Exercises 41-50, use the following graph of f...Ch. 1.1 - For Exercises 41-50, use the following graph of f...Ch. 1.1 - For Exercises 41-50, use the following graph of f...Ch. 1.1 - For Exercises 51-68, graph each function and then...Ch. 1.1 - For Exercises 51-68, graph each function and then...Ch. 1.1 - For Exercises 51-68, graph each function and then...Ch. 1.1 - For Exercises 51-68, graph each function and then...Ch. 1.1 - For Exercises 61-78, graph each function and then...Ch. 1.1 - Prob. 66ECh. 1.1 - For Exercises 61-78, graph each function and then...Ch. 1.1 - Prob. 68ECh. 1.1 - For Exercises 61-78, graph each function and then...Ch. 1.1 - Prob. 70ECh. 1.1 - For Exercises 51-68, graph each function and then...Ch. 1.1 - For Exercises 51-68, graph each function and then...Ch. 1.1 - For Exercises 51-68, graph each function and then...Ch. 1.1 - For Exercises 51-68, graph each function and then...Ch. 1.1 - For Exercises 51-68, graph each function and then...Ch. 1.1 - For Exercises 51-68, graph each function and then...Ch. 1.1 - For Exercises 51-68, graph each function and then...Ch. 1.1 - For Exercises 51-68, graph each function and then...Ch. 1.1 - Business and Economics
Taxicab fares. In New York...Ch. 1.1 - Taxicab fares. In New York City, taxicabs change...Ch. 1.1 - Taxicab fares. In New York City, taxicabs change...Ch. 1.1 - Prob. 82ECh. 1.1 - Prob. 83ECh. 1.1 - Prob. 84ECh. 1.1 - Prob. 85ECh. 1.1 - Prob. 86ECh. 1.1 - Tax rate schedule. The federal tax rate for single...Ch. 1.1 - Prob. 88ECh. 1.1 - Prob. 89ECh. 1.1 - Prob. 90ECh. 1.1 - Prob. 91ECh. 1.1 - Prob. 92ECh. 1.1 - In Exercises 83-58, fill in each blank so that...Ch. 1.1 - In Exercises 83-58, fill in each blank so that...Ch. 1.1 - In Exercises 83-58, fill in each blank so that...Ch. 1.1 - Prob. 96ECh. 1.1 - Graph the function f given by...Ch. 1.1 - In Exercises 87-89, use GRAFH and TRACE to find...Ch. 1.1 - In Exercises 87-89, use GRAFH and TRACE to find...Ch. 1.1 - In Exercises 87-89, use GRAFH and TRACE to find...Ch. 1.2 - Prob. 1ECh. 1.2 - Classify each statement as either true or...Ch. 1.2 - Classify each statement as either true or false....Ch. 1.2 - Classify each statement as either true or...Ch. 1.2 - Classify each statement as either true or false....Ch. 1.2 - Classify each statement as either true or false....Ch. 1.2 - Classify each statement as either true or...Ch. 1.2 - Classify each statement as either true or false....Ch. 1.2 - Use the theorem on limits of rational functions to...Ch. 1.2 - Use the theorem on limits of rational functions to...Ch. 1.2 - Use the theorem on limits of rational functions to...Ch. 1.2 - Use the theorem on limits of rational functions to...Ch. 1.2 - Use the theorem on limits of rational functions to...Ch. 1.2 - Use the theorem on limits of rational functions to...Ch. 1.2 - Use the theorem on limits of rational functions to...Ch. 1.2 - Use the theorem on limits of rational functions to...Ch. 1.2 - Use the theorem on limits of rational functions to...Ch. 1.2 - Use the theorem on limits of rational functions to...Ch. 1.2 - For Exercises 19-30, the initial substitution of ...Ch. 1.2 - For Exercises 19-30, the initial substitution of...Ch. 1.2 - For Exercises 19-30, the initial substitution of ...Ch. 1.2 - For Exercises 19-30, the initial substitution of ...Ch. 1.2 - For Exercises 19-30, the initial substitution of ...Ch. 1.2 - For Exercises 19-30, the initial substitution of...Ch. 1.2 - For Exercises 19-30, the initial substitution of...Ch. 1.2 - For Exercises 19-30, the initial substitution of ...Ch. 1.2 - For Exercises 19-30, the initial substitution of ...Ch. 1.2 - For Exercises 19-30, the initial substitution of...Ch. 1.2 - For Exercises 19-30, the initial substitution of ...Ch. 1.2 - For Exercises 19-30, the initial substitution of...Ch. 1.2 - Prob. 31ECh. 1.2 - Use the Limit Properties to find the following...Ch. 1.2 - Prob. 33ECh. 1.2 - Use the Limit Properties to find the following...Ch. 1.2 - Prob. 35ECh. 1.2 - Use the Limit Properties to find the following...Ch. 1.2 - Prob. 37ECh. 1.2 - Use the Limit Properties to find the following...Ch. 1.2 - Prob. 39ECh. 1.2 - Use the Limit Properties to find the following...Ch. 1.2 - Use the Limit Properties to find the following...Ch. 1.2 - Use the Limit Properties to find the following...Ch. 1.2 - Use the Limit Properties to find the following...Ch. 1.2 - Use the Limit Properties to find the following...Ch. 1.2 - Use the Limit Properties to find the following...Ch. 1.2 - Use the Limit Properties to find the following...Ch. 1.2 - Determine whether each of the function show in...Ch. 1.2 - Determine whether each of the function show in...Ch. 1.2 - Determine whether each of the function show in...Ch. 1.2 - Determine whether each of the function show in...Ch. 1.2 - Determine whether each of the function show in...Ch. 1.2 - Use the graphs and functions in Exercises 37-41 to...Ch. 1.2 - Use the graphs and functions in Exercises 37-41 to...Ch. 1.2 - Use the graphs and functions in Exercises 37-41 to...Ch. 1.2 - Use the graphs and functions in Exercises 37-41 to...Ch. 1.2 - Use the graphs and functions in Exercises 37-41 to...Ch. 1.2 - Answer Exercises 47-48 using the graph...Ch. 1.2 - Answer Exercises 47-48 using the graph...Ch. 1.2 - 49. Is the function given by continuous at ? Why...Ch. 1.2 - Is the function given by f(x)=3x2 continuous at...Ch. 1.2 - Is the function given by G(x)=1x continuous at...Ch. 1.2 - Is the function given by F(x)=x continuous at x=1?...Ch. 1.2 - Is the function given by...Ch. 1.2 - Is the function given by...Ch. 1.2 - Prob. 65ECh. 1.2 - 56. Is the function given by
Continuous at? Why...Ch. 1.2 - Is the function given by...Ch. 1.2 - Prob. 68ECh. 1.2 - 59. Is the function given by
Continuous at? Why...Ch. 1.2 - Is the function given by...Ch. 1.2 - Is the function given by...Ch. 1.2 - 62. Is the following given by
Continuous at? Why...Ch. 1.2 - Is the function given by g(x)=1x27x+10 continuous...Ch. 1.2 - 64. Is the function given by continuous at? Why...Ch. 1.2 - Is the function given by G(x)=1x26x+8 continuous...Ch. 1.2 - 66. Is the function given by continuous at? Why...Ch. 1.2 - 67. Is the function given by continuous over the...Ch. 1.2 - 68. Is the function given by continuous over the...Ch. 1.2 - Prob. 79ECh. 1.2 - Prob. 80ECh. 1.2 - Prob. 81ECh. 1.2 - Prob. 82ECh. 1.2 - Business and Economics
73. The candy factory sells...Ch. 1.2 - Business and Economics The candy Shoppe charge...Ch. 1.2 - A lab technician controls the temperature T inside...Ch. 1.2 - Prob. 86ECh. 1.2 - Prob. 87ECh. 1.2 - Prob. 88ECh. 1.2 - Prob. 89ECh. 1.2 - Prob. 90ECh. 1.2 - Prob. 91ECh. 1.2 - Prob. 92ECh. 1.2 - Prob. 93ECh. 1.2 - Prob. 94ECh. 1.2 - Prob. 95ECh. 1.2 - In Exercises 7986, find each limit. Use TABLE and...Ch. 1.2 - In Exercises 7986, find each limit. Use TABLE and...Ch. 1.2 - In Exercises 7986, find each limit. Use TABLE and...Ch. 1.2 - In Exercises 79–86, find each limit. Use TABLE and...Ch. 1.2 - In Exercises 7986, find each limit. Use TABLE and...Ch. 1.2 - In Exercises 79–86, find each limit. Use TABLE and...Ch. 1.2 - In Exercises 7986, find each limit. Use TABLE and...Ch. 1.2 - In Exercises 79–86, find each limit. Use TABLE and...Ch. 1.3 - In Exercises 1-10, state the average rate of...Ch. 1.3 - In Exercises 1-10, state the average rate of...Ch. 1.3 - In Exercises 110, state the average rate of change...Ch. 1.3 - Prob. 4ECh. 1.3 - Prob. 5ECh. 1.3 - Prob. 6ECh. 1.3 - Prob. 7ECh. 1.3 - Prob. 8ECh. 1.3 - In Exercises 1-10, state the average rate of...Ch. 1.3 - Prob. 10ECh. 1.3 - In Exercises 11-20, find the average rate of...Ch. 1.3 - In Exercises 11-20, find the average rate of...Ch. 1.3 - Prob. 13ECh. 1.3 - In Exercises 11-20, find the average rate of...Ch. 1.3 - In Exercises 11-20, find the average rate of...Ch. 1.3 - In Exercises 11-20, find the average rate of...Ch. 1.3 - Prob. 17ECh. 1.3 - In Exercises 11-20, find the average rate of...Ch. 1.3 - In Exercises 11-20, find the average rate of...Ch. 1.3 - In Exercises 11-20, find the average rate of...Ch. 1.3 - Prob. 21ECh. 1.3 - For each function in Exercises 21-36, (a) find the...Ch. 1.3 - Prob. 23ECh. 1.3 - For each function in Exercises 21-36, (a) find the...Ch. 1.3 - Prob. 25ECh. 1.3 - For each function in Exercises 21-36, (a) find the...Ch. 1.3 - For each function in Exercises 21-36, (a) find the...Ch. 1.3 - For each function in Exercises 21-36, (a) find the...Ch. 1.3 - Prob. 29ECh. 1.3 - For each function in Exercises 21-36, (a) find the...Ch. 1.3 - Prob. 31ECh. 1.3 - For each function in Exercises 21-36, (a) find the...Ch. 1.3 - Prob. 33ECh. 1.3 - For each function in Exercises 21-36, (a) find the...Ch. 1.3 - Prob. 35ECh. 1.3 - For each function in Exercises 21-36, (a) find the...Ch. 1.3 - For Exercises 37-44, use each graph to estimate...Ch. 1.3 - For Exercises 37-44, use each graph to estimate...Ch. 1.3 - Prob. 39ECh. 1.3 - For Exercises 37-44, use each graph to estimate...Ch. 1.3 - For Exercises 37-44, use each graph to estimate...Ch. 1.3 - For Exercises 37-44, use each graph to estimate...Ch. 1.3 - Prob. 43ECh. 1.3 - For Exercises 37-44, use each graph to estimate...Ch. 1.3 - Prob. 45ECh. 1.3 - Use the following graph to find the average rate...Ch. 1.3 - 27. Utility. Utility is a type of function that...Ch. 1.3 - 28. Advertising results. The following graph shows...Ch. 1.3 - Total cost. Suppose Fast Trends determines that...Ch. 1.3 - Total revenue. Suppose Fast Trends determines that...Ch. 1.3 - Home range. It has been show that the home range,...Ch. 1.3 - Gas mileage. At the beginning of a trip, the...Ch. 1.3 - Average velocity. In second, an object dropped...Ch. 1.3 - Prob. 60ECh. 1.3 - 43. Population growth. The two curves below...Ch. 1.3 - Find the simplified difference quotient for each...Ch. 1.3 - Find the simplified difference quotient for each...Ch. 1.3 - Find the simplified difference quotient for each...Ch. 1.3 - Find the simplified difference quotient for each...Ch. 1.3 - Find the simplified difference quotient for each...Ch. 1.3 - Find the simplified difference quotient for each...Ch. 1.3 - Find the simplified difference quotient for each...Ch. 1.3 - Find the simplified difference quotient for each...Ch. 1.3 - For Exercises 55 and 56, find the simplified...Ch. 1.3 - For Exercises 55 and 56, find the simplified...Ch. 1.4 - In Exercises 1-16;
a. a) Graph the...Ch. 1.4 - In Exercises 1-16;
a. a) Graph the...Ch. 1.4 - a.Graph the function. b.Draw tangent lines to the...Ch. 1.4 - In Exercises 1-16;
a. a) Graph the...Ch. 1.4 - In Exercises 1-16;
a. a) Graph the...Ch. 1.4 - In Exercises 1-16;
a. a) Graph the...Ch. 1.4 - a.Graph the function. b.Draw tangent lines to the...Ch. 1.4 - In Exercises 1-16;
a. a) Graph the...Ch. 1.4 - In Exercises 1-16;
a. a) Graph the...Ch. 1.4 - a.Graph the function. b.Draw tangent lines to the...Ch. 1.4 - a. a) Graph the function. b. b) Draw tangent lines...Ch. 1.4 - a. a) Graph the function. b. b) Draw tangent lines...Ch. 1.4 - a. a) Graph the function. b. b) Draw tangent lines...Ch. 1.4 - a. a) Graph the function. b. b) Draw tangent lines...Ch. 1.4 - a.Graph the function. b.Draw tangent lines to the...Ch. 1.4 - a. a) Graph the function. b. b) Draw tangent lines...Ch. 1.4 - 17. Find an equation of the tangent line to the...Ch. 1.4 - 18. Find an equation of the tangent line to the...Ch. 1.4 - 19. Find an equation of the tangent line to the...Ch. 1.4 - 20. Find an equation of the tangent line to the...Ch. 1.4 - 21. Find an equation of the tangent line to the...Ch. 1.4 - 22. Find an equation of the tangent line to the...Ch. 1.4 - Find f(x) for f(x)=mx+b.Ch. 1.4 - Find f(x) for f(x)=ax2+bx.Ch. 1.4 - 29. Draw a graph that is continuous, but not...Ch. 1.4 - Draw a graph that is continuous, with no corners,...Ch. 1.4 - 31. Draw a graph that has a horizontal tangent...Ch. 1.4 - Draw a graph that is differentiable and has...Ch. 1.4 - Draw a graph that has horizontal tangent lines at...Ch. 1.4 - Draw a graph that is continuous for all x, with no...Ch. 1.4 - Prob. 38ECh. 1.4 - In Exercises 39-42, classify each statement as...Ch. 1.4 - Prob. 40ECh. 1.4 - Prob. 42ECh. 1.4 - Prob. 43ECh. 1.4 - For Exercises 45-51, find f(x) for the given...Ch. 1.4 - Prob. 46ECh. 1.4 - Prob. 47ECh. 1.4 - Prob. 48ECh. 1.4 - For Exercises 45-51, find f(x) for the given...Ch. 1.4 - Prob. 50ECh. 1.4 - Prob. 51ECh. 1.4 - Prob. 52ECh. 1.4 - Prob. 53ECh. 1.4 - Prob. 54ECh. 1.4 - Prob. 55ECh. 1.4 - 54. Let. A student graphs this function, and the...Ch. 1.4 - Let F be a function given by...Ch. 1.4 - Let G be a function given by...Ch. 1.4 - Let H be a function given by...Ch. 1.4 - Prob. 64ECh. 1.5 - For the function given by u=f(v), write four...Ch. 1.5 - Prob. 2ECh. 1.5 - Prob. 3ECh. 1.5 - Prob. 4ECh. 1.5 - For the function given by h=m(k), write four...Ch. 1.5 - Prob. 6ECh. 1.5 - Find dydx. y=x7Ch. 1.5 - Find dydx. y=x8Ch. 1.5 - Find.
4.
Ch. 1.5 - Find.
3.
Ch. 1.5 - Find.
6.
Ch. 1.5 - Find.
5.
Ch. 1.5 - Find.
8.
Ch. 1.5 - Find.
7.
Ch. 1.5 - Find dydx. y=x6Ch. 1.5 - Find.
9.
Ch. 1.5 - Find.
12.
Ch. 1.5 - Find dydx. y=3x5Ch. 1.5 - Find dydx. y=x3+3x2Ch. 1.5 - Find.
13.
Ch. 1.5 - Find.
16.
Ch. 1.5 - Find.
15.
Ch. 1.5 - Find.
18.
Ch. 1.5 - Prob. 24ECh. 1.5 - Find.
20.
Ch. 1.5 - Find.
19.
Ch. 1.5 - Find.
22.
Ch. 1.5 - Find.
21.
Ch. 1.5 - Find each derivative.
25.
Ch. 1.5 - Find each derivative. ddx(x3+4x)Ch. 1.5 - Find each derivative.
27.
Ch. 1.5 - Find each derivative. ddx(x34)Ch. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Find each derivative. 35. f(x)=25x6Ch. 1.5 - Prob. 36ECh. 1.5 - Find each derivative. 37. f(x)=4xx3/5Ch. 1.5 - Prob. 38ECh. 1.5 - Find g(x). 39. g(x)=7x14Ch. 1.5 - Prob. 40ECh. 1.5 - Find g(x). 41. g(x)=x3/23Ch. 1.5 - Prob. 42ECh. 1.5 - Find f(x). f(x)=0.01x2+0.4x+500.02x+0.4Ch. 1.5 - Find f(x). f(x)=0.01x20.5x+700.02x0.5Ch. 1.5 - Find y y=x3/43x2/3+x5/4+2x434x7/42x1/3+54x1/48x5Ch. 1.5 - Find
46.
Ch. 1.5 - Find y y=x7+7xCh. 1.5 - Find
48.
Ch. 1.5 - Find y If f(x)=x,findf(4).Ch. 1.5 - Find
50. If.
Ch. 1.5 - If y=x+2x3, find dydx at x=1.Ch. 1.5 - If y=4x2, find dydx at x=2.Ch. 1.5 - If y=x3+x, find dydx at x=64.Ch. 1.5 - Prob. 54ECh. 1.5 - If y=25x3, find dydx at x=4.Ch. 1.5 - Prob. 56ECh. 1.5 - 57. Find an equation of the tangent line to the...Ch. 1.5 - Find an equation (in y=mx+b form) of the tangent...Ch. 1.5 - 59. Find an equation of the tangent line to the...Ch. 1.5 - Find an equation of the tangent line to the graph...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each function, find the point on the graph at...Ch. 1.5 - For each the function, find the point on the graph...Ch. 1.5 - For each the function, find the point on the graph...Ch. 1.5 - For each the function, find the point on the graph...Ch. 1.5 - For each the function, find the point on the graph...Ch. 1.5 - For each the function, find the point on the graph...Ch. 1.5 - For each the function, find the point on the graph...Ch. 1.5 - Prob. 85ECh. 1.5 - Prob. 86ECh. 1.5 - Growth of a child. The median weight of a boy...Ch. 1.5 - Prob. 88ECh. 1.5 - Prob. 90ECh. 1.5 - Population growth rate. In t year, the population...Ch. 1.5 - Prob. 93ECh. 1.5 - Prob. 94ECh. 1.5 - For Exercises 95 and 96, find the interval(s) for...Ch. 1.5 - For Exercises 95 and 96, find the interval(s) for...Ch. 1.5 - Find the points on the graph of y=x443x24 at which...Ch. 1.5 - Find the point on the graph of y=2x6x42 at which...Ch. 1.5 - 101. Use the derivative to help explain why ...Ch. 1.5 - Use the derivative to help explain why f(x)=x3+ax...Ch. 1.5 - Find Each function can be different using the...Ch. 1.5 - Prob. 105ECh. 1.5 - Find dy/dx Each function can be different using...Ch. 1.5 - Find dy/dx Each function can be different using...Ch. 1.5 - Find Each function can be different using the...Ch. 1.5 - Find Each function can be different using the...Ch. 1.5 - Find Each function can be different using the...Ch. 1.5 - Find dy/dx Each function can be different using...Ch. 1.5 - Prob. 113ECh. 1.5 - Prob. 114ECh. 1.5 - Prob. 115ECh. 1.5 - Prob. 116ECh. 1.5 - Prob. 117ECh. 1.5 - Prob. 118ECh. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate two ways; first, by using the...Ch. 1.6 - Differentiate each function.
22.
Ch. 1.6 - Differentiate each function....Ch. 1.6 - Differentiate each function. y=5x212x3+3Ch. 1.6 - Differentiate each function.
24.
Ch. 1.6 - Differentiate each function. G(x)=(8x+x)(5x2+3)Ch. 1.6 - Differentiate each function.
25.
Ch. 1.6 - Differentiate each function.
27.
Ch. 1.6 - Differentiate each function. f(t)=t5+2t2t4Ch. 1.6 - Differentiate each function.
30.
[Hint: ]
Ch. 1.6 - Differentiate each function. G(x)=(5x4)2Ch. 1.6 - Differentiate each function. y=(x34x)2Ch. 1.6 - Differentiate each function. y=(3x24x+5)2Ch. 1.6 - Differentiate each function.
34.
Ch. 1.6 - Differentiate each function....Ch. 1.6 - Differentiate each function. F(t)=(t+2t)(t23)Ch. 1.6 - Differentiate each function. G(x)=(3t5t2)(t5t)Ch. 1.6 - Differentiate each function. y=x2+1x315x2Ch. 1.6 - Differentiate each function. y=x31x2+1+4x3Ch. 1.6 - Differentiate each function.
39.
Ch. 1.6 - Differentiate each function. y=x+4x35Ch. 1.6 - Differentiate each function. f(x)=xx1+1Ch. 1.6 - Differentiate each function. f(x)=x1x+x1Ch. 1.6 - Differentiate each function. F(t)=1t4Ch. 1.6 - Differentiate each function.
44.
Ch. 1.6 - Differentiate each function.
46.
Ch. 1.6 - Differentiate each function. f(x)=3x25xx21Ch. 1.6 - Differentiate each function. g(x)=t2+3t+5t2+2t+4Ch. 1.6 - Differentiate each function.
48.
Ch. 1.6 - Find an equation of the tangent line to the graph...Ch. 1.6 - 49. Find an equation of the tangent line to the...Ch. 1.6 - Find an equation of the tangent line to the graph...Ch. 1.6 - 51. Find an equation of the tangent line to the...Ch. 1.6 - Average cost. Prestons Leatherworks finds that...Ch. 1.6 - 54. Average cost. Tongue-Tied Sauces, Inc, finds...Ch. 1.6 - Average revenue. Prestons Leatherworks find that...Ch. 1.6 - 56. Average revenue. Tongue-Tied Sauces, Inc,...Ch. 1.6 - Average profit. Use the information in Exercises...Ch. 1.6 - Average profit. Use the information in exercises...Ch. 1.6 - 59. Average profit. Sparkle pottery has determined...Ch. 1.6 - 60. Average profit. Cruzin’ Boards has found that...Ch. 1.6 - Prob. 61ECh. 1.6 - Temperature during an illness. Ginas temperature T...Ch. 1.6 - Prob. 63ECh. 1.6 - Prob. 64ECh. 1.6 - Differentiate each function.
64. (Hint: Simplify...Ch. 1.6 - Differentiate each function.
65.
Ch. 1.6 - Differentiate each function.
66.
Ch. 1.6 - Differentiate each function. g(x)=(x38)x2+1x21Ch. 1.6 - Let f(x)=xx+1 and g(x)=1x+1. a. Compute f(x). b....Ch. 1.6 - 71. Let and .
a. Compute .
b. Compute .
c. c)...Ch. 1.6 - Write a rule for finding the derivative of...Ch. 1.6 - Is the derivative of the reciprocal of f(x) the...Ch. 1.6 - Sensitivity. The reaction R of the body to a dose...Ch. 1.6 - 75. A proof of the Product Rule appears below....Ch. 1.6 - 76. Business. Refer to Exercises 54, 56, and 58....Ch. 1.6 - Prob. 76ECh. 1.6 - For the function in each of Exercises 78-83, graph...Ch. 1.6 - For the function in each of Exercises 78-83, graph...Ch. 1.6 - For the function in each of Exercises 78-83, graph...Ch. 1.6 - For the function in each of Exercises 78-83, graph...Ch. 1.6 - Prob. 81ECh. 1.7 - Differentiate each function using the Chain Rule....Ch. 1.7 - Prob. 2ECh. 1.7 - Prob. 3ECh. 1.7 - Prob. 4ECh. 1.7 - Differentiate each function using the Chain Rule....Ch. 1.7 - Prob. 6ECh. 1.7 - Prob. 7ECh. 1.7 - Prob. 8ECh. 1.7 - Differentiate each function using the Chain Rule....Ch. 1.7 - Prob. 10ECh. 1.7 - Differentiate each function using the Chain Rule....Ch. 1.7 - Prob. 12ECh. 1.7 - Prob. 13ECh. 1.7 - Differentiate each function using the Chain Rule....Ch. 1.7 - Differentiate each function using the Chain Rule....Ch. 1.7 - Prob. 16ECh. 1.7 - Prob. 17ECh. 1.7 - Prob. 18ECh. 1.7 - Prob. 19ECh. 1.7 - Differentiate each function using the Chain Rule....Ch. 1.7 - Differentiate each function using the Chain Rule....Ch. 1.7 - Prob. 22ECh. 1.7 - Prob. 23ECh. 1.7 - Differentiate each function using the Chain Rule....Ch. 1.7 - Differentiate each function using the Chain Rule....Ch. 1.7 - Prob. 26ECh. 1.7 - Prob. 27ECh. 1.7 - Prob. 28ECh. 1.7 - Prob. 29ECh. 1.7 - Prob. 30ECh. 1.7 - Differentiate each function using the Chain Rule....Ch. 1.7 - Prob. 32ECh. 1.7 - Find .
45.
Ch. 1.7 - Prob. 34ECh. 1.7 - Find .
47.
Ch. 1.7 - Find .
48.
Ch. 1.7 - Find dydx for each pair of functions....Ch. 1.7 - Find for each pair of functions.
52.
Ch. 1.7 - Find dydx for each pair of functions. Find...Ch. 1.7 - Prob. 40ECh. 1.7 - 57. Find an equation for the tangent line to the...Ch. 1.7 - Find an equation for the tangent line to the graph...Ch. 1.7 - 59. Find an equation for the tangent line to the...Ch. 1.7 - 60. Find an equation for the tangent line to the...Ch. 1.7 - Consider g(x)=(6x+12x5)2. a. Find g(x) using the...Ch. 1.7 - 62. Consider
.
a. Find using the Quotient and...Ch. 1.7 - 63. Let .
Find .
Ch. 1.7 - Let f(u)=u+1u1andg(x)=u=x. Find (fg)(4).Ch. 1.7 - Let f(u)=u3andg(x)=u=1+3x2. Find (fg)(2).Ch. 1.7 - 66. Let .
Find .
Ch. 1.7 - Let h(x)=3x2+2x5. Find functions f and g such that...Ch. 1.7 - Prob. 52ECh. 1.7 - Prob. 53ECh. 1.7 - Prob. 54ECh. 1.7 - Prob. 55ECh. 1.7 - Prob. 56ECh. 1.7 - Prob. 57ECh. 1.7 - Prob. 58ECh. 1.7 - Total revenue. A total-revenue function is given...Ch. 1.7 - Total cost. A total-cost function is given by...Ch. 1.7 - Total profit. Use the total-cost and total-revenue...Ch. 1.7 - Total cost. Solid Seats, Inc., determines that its...Ch. 1.7 - Compound interest. If 1000 is invested at interest...Ch. 1.7 - Prob. 64ECh. 1.7 - 79. Business profit. French’s Electronics is...Ch. 1.7 - Consumer demand. Suppose the demand function for a...Ch. 1.7 - Chemotherapy. The dosage for Carboplatin...Ch. 1.7 - Prob. 68ECh. 1.7 - Prob. 69ECh. 1.7 - Prob. 70ECh. 1.7 - Prob. 71ECh. 1.7 - Prob. 72ECh. 1.7 - Prob. 73ECh. 1.7 - Prob. 74ECh. 1.7 - Differentiate.
87.
Ch. 1.7 - Prob. 76ECh. 1.7 - Differentiate. y=1x21xCh. 1.7 - Differentiate. y=(x2x1x2+1)3Ch. 1.7 - Differentiate.
92.
Ch. 1.7 - Prob. 80ECh. 1.7 - Prob. 81ECh. 1.7 - Prob. 82ECh. 1.7 - Prob. 83ECh. 1.7 - For the function in each of Exercises 97 and 98,...Ch. 1.7 - For the function in each of Exercises 97 and 98,...Ch. 1.8 - Find d2y/dx2. y=x5+9Ch. 1.8 - Find .
1.
Ch. 1.8 - Find .
4.
Ch. 1.8 - Find .
3.
Ch. 1.8 - Find d2y/dx2. y=4x2+3x1Ch. 1.8 - Find .
5.
Ch. 1.8 - Find d2y/dx2. y=6x3Ch. 1.8 - Find d2y/dx2. y=7x+2Ch. 1.8 - Find .
10.
Ch. 1.8 - Find .
9.
Ch. 1.8 - Find d2y/dx2. y=x4Ch. 1.8 - Find .
11.
Ch. 1.8 - Find f(x). f(x)=x4+3xCh. 1.8 - Find f(x). f(x)=x35xCh. 1.8 - Find .
16.
Ch. 1.8 - Find .
15.
Ch. 1.8 - Find f(x). f(x)=4x3Ch. 1.8 - Find .
17.
Ch. 1.8 - Find f(x). f(x)=(x3+2x)6Ch. 1.8 - Find .
19.
Ch. 1.8 - Find .
23.
Ch. 1.8 - Find f(x). f(x)=(x21)23Ch. 1.8 - Find y. y=x3/25xCh. 1.8 - Find y. y=x2/3+4xCh. 1.8 - Find y. y=(x3x)3/4Ch. 1.8 - Find y. y=(x4+x)2/3Ch. 1.8 - Find y. y=3x+12x3Ch. 1.8 - Find y. y=2x+35x1Ch. 1.8 - For y=x5, find d4y/dx4.Ch. 1.8 - 38. For , find .
Ch. 1.8 - 39. For , find .
Ch. 1.8 - 40. For , find .
Ch. 1.8 - 41. For , find .
Ch. 1.8 - For f(x)=x2x1/2, find f(4)(x).Ch. 1.8 - Given s(t)=t3+t where s(t) is in feet and t is in...Ch. 1.8 - Given s(t)=10t2+2t+5, where s(t) is in meters and...Ch. 1.8 - 48. Given
,
where is in meters and t is in...Ch. 1.8 - 47. Given
,
where is in miles and t is in hours,...Ch. 1.8 - Free fall. When an object is dropped the distance...Ch. 1.8 - Prob. 40ECh. 1.8 - Free fall. Find the velocity and acceleration of...Ch. 1.8 - 52. Free fall. Find the velocity and acceleration...Ch. 1.8 - 53. The following graph describes a bicycle...Ch. 1.8 - The following graph describes an airplanes...Ch. 1.8 - Sales. The following graph represents the sales,...Ch. 1.8 - Velocity and acceleration. The following graph...Ch. 1.8 - 57. Sales. A company determine that monthly sales...Ch. 1.8 - Sales. Nadias fashions discovers that the number...Ch. 1.8 - Population. The function P(t)=2000t4t+75 gives the...Ch. 1.8 - 60. Medicine. A medication is injected into the...Ch. 1.8 - Prob. 51ECh. 1.8 - Prob. 52ECh. 1.8 - Prob. 53ECh. 1.8 - Prob. 54ECh. 1.8 - Prob. 55ECh. 1.8 - Prob. 56ECh. 1.8 - Prob. 57ECh. 1.8 - Prob. 58ECh. 1.8 - Prob. 59ECh. 1.8 - Prob. 60ECh. 1.8 - Prob. 61ECh. 1.8 - Prob. 62ECh. 1.8 - Free fall. On the moon, all free-fall distance...Ch. 1.8 - Prob. 64ECh. 1.8 - Prob. 65ECh. 1.8 - A bicyclists distance from her starting point is...Ch. 1.8 - Prob. 67ECh. 1.8 - Prob. 68ECh. 1.8 - Prob. 69ECh. 1.8 - Prob. 70ECh. 1.8 - For the distance function in each of Exercises...Ch. 1.8 - For the distance function in each of Exercises...Ch. 1 - Classify each statement as either true or false....Ch. 1 - Classify each statement as either true or false....Ch. 1 - Classify each statement as either true or...Ch. 1 - Classify each statement as either true or...Ch. 1 - Classify each statement as either true or...Ch. 1 - Classify each statement as either true or...Ch. 1 - Classify each statement as either true or...Ch. 1 - Classify each statement as either true or...Ch. 1 - Match each function in column A with the most...Ch. 1 - Match each function in column A with the most...Ch. 1 - Match each function in column A with the most...Ch. 1 - Match each function in column A with the most...Ch. 1 - Match each function in column A with the most...Ch. 1 - Match each function in column A with the most...Ch. 1 - For Exercises 15-17, consider...Ch. 1 - For Exercises 15-17, consider...Ch. 1 - For Exercises 15-17, consider
.
17. Limit...Ch. 1 - Find each limit, if it exists. If a limit does not...Ch. 1 - Find each limit, if it exists. If a limit does not...Ch. 1 - Find each limit, if it exists. If a limit does not...Ch. 1 - Find each limit, if it exists. If a limit does not...Ch. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - For Exercises 22-30, consider the function g...Ch. 1 - For Exercises 22-30, consider the function g...Ch. 1 - For Exercises 22-30, consider the function g...Ch. 1 - For Exercises 22-30, consider the function g...Ch. 1 - For Exercises 22-30, consider the function g...Ch. 1 - For Exercises 22-30, consider the function g...Ch. 1 - For Exercises 22-30, consider the function g...Ch. 1 - For Exercises 22-30, consider the function g...Ch. 1 - For Exercises 22-30, consider the function g...Ch. 1 - For Exercises 31-34, consider the function f...Ch. 1 - For Exercises 31-34, consider the function f...Ch. 1 - For Exercises 31-34, consider the function f...Ch. 1 - For Exercises 31-34, consider the function f...Ch. 1 - 35. For find the average rate of change as x...Ch. 1 - Find a simplified difference quotient for...Ch. 1 - 37. Find a simplify difference quotient for
.
Ch. 1 - 38. Find an equation of the tangent line to the...Ch. 1 - Find .
41.
Ch. 1 - Find dy/dx. y=8x3 [1.5]Ch. 1 - Find .
43.
Ch. 1 - Find dy/dx. y=15x2/5 [1.5]Ch. 1 - Find .
45.
Ch. 1 - Differentiate. f(x)=512x6+8x42x [1.5]Ch. 1 - Differentiate.
47.
Ch. 1 - Differentiate. y=x2+88x [1.6]Ch. 1 - Differentiate.
49.
Ch. 1 - Differentiate. f(x)=(x53)7 [1.7]Ch. 1 - Differentiate. f(x)=x2(4x+2)3/4 [1.7]Ch. 1 - 52. For .
Ch. 1 - For y=342x710x3+13x2+28x2,findy. [1.8]Ch. 1 - Prob. 56RECh. 1 - For Exercises 55-58, consider the growth of , the...Ch. 1 - For Exercises 55-58, consider the growth of , the...Ch. 1 - For Exercises 55-58, consider the growth of...Ch. 1 - For Exercises 55-58, consider the growth of...Ch. 1 - Prob. 61RECh. 1 - Business: average revenue, cost, and profit. Given...Ch. 1 - Find ddx(fg)(x) and ddx(gf)(x), given f(x)=x2+5...Ch. 1 - Prob. 64RECh. 1 - Prob. 65RECh. 1 - Prob. 66RECh. 1 - Prob. 67RECh. 1 - Prob. 68RECh. 1 - For Exercises 1-3, consider
,
1. Numerical...Ch. 1 - For Exercises 1-3, consider...Ch. 1 - For Exercises 1-3, consider...Ch. 1 - Graphical limits. For Exercises 4-15, consider the...Ch. 1 - Prob. 5TCh. 1 - Prob. 6TCh. 1 - Prob. 7TCh. 1 - Prob. 8TCh. 1 - Prob. 9TCh. 1 - Prob. 10TCh. 1 - Prob. 11TCh. 1 - Graphical limits. For Exercises 4-15, consider the...Ch. 1 - Prob. 13TCh. 1 - Determine whether each function is continuous. If...Ch. 1 - Determine whether each function is continuous. If...Ch. 1 - For Exercises 18 and 19, consider the function...Ch. 1 - For Exercises 18 and 19, consider the function...Ch. 1 - Find each limit, if it exists. If a limit does not...Ch. 1 - Find each limit, if it exists. If a limit does not...Ch. 1 - Find each limit, if it exists. If a limit does not...Ch. 1 - Find the simplified difference quotient for...Ch. 1 - Find an equation of the line tangent to y=x+(4/x)...Ch. 1 - 25. Find the point(s) on the graph of at which...Ch. 1 - Find dy/dx y=x23Ch. 1 - Find
27.
Ch. 1 - Find dy/dx y=10xCh. 1 - Find dy/dx y=x5/4Ch. 1 - Find dy/dx y=0.5x2+0.61x+90Ch. 1 - Differentiate y=13x3x2+2x+4Ch. 1 - Differentiate
32.
Ch. 1 - Differentiate f(x)=x5xCh. 1 - Differentiate f(x)=(x+3)4(7x)5Ch. 1 - Differentiate y=(x54x3+x)5Ch. 1 - Differentiate
36.
Ch. 1 - Differentiate For y=x43x2 find d3ydx3.Ch. 1 - 38. Social science: memory. In a certain memory...Ch. 1 - Business: average revenue, cost, and profit. Given...Ch. 1 - For Exercises 40 and 41, let and .
40. Find
Ch. 1 - For Exercises 40 and 41, let f(x)=x2x and...Ch. 1 - A ball is placed on an inclined plane and, due to...Ch. 1 - Prob. 43TCh. 1 - Find limx3x327x3.Ch. 1 - Prob. 45TCh. 1 - Find the following limit by creating a table of...Ch. 1 - Plot the points and connect them with line...Ch. 1 - Prob. 6ETECh. 1 - Prob. 7ETECh. 1 - Prob. 8ETE
Additional Math Textbook Solutions
Find more solutions based on key concepts
Continuity at a point Determine whether the following functions are continuous at a. Use the continuity checkli...
Calculus: Early Transcendentals (2nd Edition)
Identifying surfaces Identify and briefly describe the surfaces defined by the following equations. 86.x2 + 4y2...
Calculus: Early Transcendentals (2nd Edition)
Fill in each blanks so that the resulting statement is true. Any set of ordered pairs is called a/an _______. T...
College Algebra (7th Edition)
Here is the region of integration of the integral
Rewrite the integral as an equivalent iterated integral in ...
University Calculus: Early Transcendentals (4th Edition)
Constructing and Graphing Discrete Probability Distributions In Exercises 19 and 20, (a) construct a probabilit...
Elementary Statistics: Picturing the World (7th Edition)
CHECK POINT I Let p and q represent the following statements: p : 3 + 5 = 8 q : 2 × 7 = 20. Determine the truth...
Thinking Mathematically (6th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- し ined sove in peaper Anot in PV+96252 √4-x²-y² Q4// Convert √ √ √2x-x2 √√4-x-2_ 21xy² dzdydx to (a) cylindrical coordinates, (b) Spherical coordinates. ln3 (m3)2-x2 Q Draw and Evaluate Lake √x²+ dydarrow_forward: +0 1 R2X2 العنوان I need a detailed drawing with explanation L L 2) slots per pole per phase = 3/31 B = 180-60 msl Kd Kol, Sin (Info) Isin (6) sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120 x 50 6 50105 1000 S=1000-950 Loco mem 6. Copper losses: 5kw Rotor input loo kw 0.05 اذا ميريد شرح الكتب فقط look 7) rotor DC ined sove in peaper PU + 96er Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 5100 2n=2√²+n Lake Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. T (3n)! 00 //Σn=1 (1+n)!(2+n)!" TH Marrow_forward۳/۱ : +♡ العنوان R2 X2 2) slots per pole per phase = 3/31 B-180-60 msl Kd Kas Sin (1) Isin (6) sin(30) Sin (30) اذا ميريد شرح الكتب بس بالفراغ 3) Cos (30) 0.866 レ× 4) Rotating 5) Synchronous speed, 120 x 50 G S=1000-950 50105 1000 looo rem > ined sove in pea Copper losses 5kw Rotor input: 5 0.05 (lookw) bos cid PU+965 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the series' convergence if possible. 7) rotor !!Σn=1 (1-1)" が Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the series' convergence if possible. 5700 Prove that the p-series Σn=11 (p areal constant) converges if, and diverges otherwise. T Τ Lake Marrow_forward
- Vo)) %TV .. + 1 R2X2 2) slots per pole per phase = 3/31 B-180-60 msl Kol Sin () Isin () Kd تب بس بالفراغ i Cos (30) 0.866 4) Rotating ۳/۱ 5) Synchronous speed; 12 S=1000-950 50 1000 Copper losses: 5kw Rotor input 5 loo kw 0.05 6) I العنوان Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the series' convergence if possible. اذا ميريد شرح الكتب فقط ok 7) rotor ||| DC 11500 30tan¹() 2n=1' m²+1 1:11 > PV + 16°52 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the series' convergence if possible. 7357 //Σm=1 (m²-5n+6) Lake Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the series' convergence if possible. - (3)(5+)) T d sove in peaper =T Marrow_forwardL ined sove in peaper Anoting PU+965 4 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. +1Σm=1 00 sin Sn Lake 55 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 5700 2n=2√2+n Carrow_forwardMinistry of Higher Education & Scientific Research Babylon University College of Engineering- musayab Homobile Department Subject :Numerical Analyses Stage: Third Time: 90 min Date: 25-4-2023 2nd month exam/2nd semester (2022-2023) Note: Answer all questions, all questions have same degree. Q1:Given the values X 5 7 11 13 17 F(x) 150 392 1452 2366 5202 Evaluate f(9),using Newton's divided difference formula Q2:A slider in a machine moves along a fixed straight rod.its distance (x cm) along the rod is given below for various values of the time.Find the velocity and acceleration of the slider when t=0.3 seconds. t(seconds) 0 X (cm) 30.13 0.1 31.62 0.2 0.3 0.4 0.5 0.6 32.87 33.64 33.95 33.81 33.24 Q3:From the following table,find the area bounded by the curve and x- axis,between the ordinates x=7.74 to x=7.52 using Simpson's 1/3 rule. X y=f(x) 7.47 7.48 1.93 1.95 7.49 1.98 7.50 7.51 7.52 2.01 2.03 2.06 Q4:Given y+x with initial condition y=1 at x=0;find (y) for x=0.1 by Euler's method.…arrow_forward
- V ined sove in peaper Pu+96er Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 21/11 55 a Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 1Σn=1 (2-") n° 3" 6"arrow_forwardL ined sove in peaper Anoting PU+965 4 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. +1Σm=1 00 sin Sn Lake 55 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 5700 2n=2√2+n Carrow_forwarda い पीर ined sove in peaper Pu+9625 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 3" 6" 1Σn=1 (2-") n Lake = Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum 1/n 2" (n-√n -n 2n-1 0 T=1 . if possible.arrow_forward
- Anot ined sove in peaper +9198 PU+965 Q3// Draw and Evaluate fƒ³½³¸ x/3 x -dydx x²+y2 Lake Gart Draw and Find the centroid of the region between the parabola x + y² - 4y=0 and the 2x+y=0 in the xy-plane 3+arrow_forward: +0 العنوان I need a detailed drawing with explanation しじ ined sove in peaper Anoting Q4// Draw and Evaluate √√√xy-²sin(y²)dydx PU+96er Lake Ge Q3// Find the volume of the region between the cylinder 2 = y² and the xy- plane that is bounded by the planes x = 1, x = 2, y = -2, and y = 2. T Marrow_forwardUniversity of Babylon Faculty of Engineering-AIMusyab Automobile Eng. Dep. Year: 2022-2023, 2 Course, 1 Attempt Note: Answer five questions only. Stage Third Subject: Numerical Analysis Date: 2023\\ Time: 3 Hour Q1: Solve the poisson equation [Uxx + Uyy = -81xy), [arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Limits and Continuity; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9brk313DjV8;License: Standard YouTube License, CC-BY