
Concept explainers
(a)
To Calculate:The magnitude of gravitational force due to
(a)
Answer to Problem 74P
Explanation of Solution
Given data:
Radius of
Center has shifted,
Formula Used:
Gravitational field:
Where, G is the gravitational constant, m is the mass and r is the distance of the point where field is calculated.
The gravitational force is a force of attraction between any two bodies having mass and separated by a distance d . Mathematically, the gravitational force can be represented by:
Where, G is the gravitational constant, m and M are the masses and r is the distance between them.
Calculation:
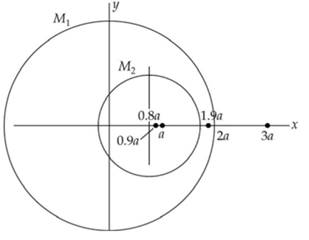
The magnitude of force due to
Again, due to
Force,
Hence, net force
At
Conclusion:
Thus, the magnitude of gravitational force due to
(b)
The magnitude of gravitational force due to
(b)
Answer to Problem 74P
Explanation of Solution
Given data:
Radius of
Center has shifted,
Formula Used:
Gravitational field:
Where, G is the gravitational constant, m is the mass and r is the distance of the point where field is calculated.
The gravitational force is a force of attraction between any two bodies having mass and separated by a distance d . Mathematically, the gravitational force can be represented by:
Where, G is the gravitational constant, m and M are the masses and r is the distance between them.
Calculation:
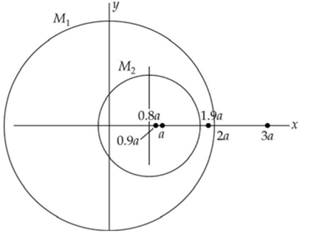
The value of
Hence,
The value of
Hence, net force
Conclusion:
Thus, the magnitude of gravitational force due to
(c)
The magnitude of gravitational force due to
(c)
Answer to Problem 74P
Explanation of Solution
Given data:
Radius of
Center has shifted,
Formula Used:
Gravitational field:
Where, G is the gravitational constant, m is the mass and r is the distance of the point where field is calculated.
The gravitational force is a force of attraction between any two bodies having mass and separated by a distance d . Mathematically, the gravitational force can be represented by:
Where, G is the gravitational constant, m and M are the masses and r is the distance between them.
Calculation:
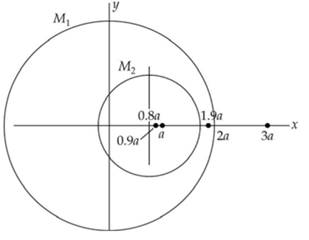
The value of
Again, the value of
So,
Hence, net force
Conclusion:
Thus, the magnitude of gravitational force due to
Want to see more full solutions like this?
Chapter 11 Solutions
Physics for Scientists and Engineers
- (Figure 1)In each case let w be the weight of the suspended crate full of priceless art objects. The strut is uniform and also has weight w Find the direction of the force exerted on the strut by the pivot in the arrangement (a). Express your answer in degrees. Find the tension Tb in the cable in the arrangement (b). Express your answer in terms of w. Find the magnitude of the force exerted on the strut by the pivot in the arrangement (b). Express your answer in terms of w.arrow_forward(Figure 1)In each case let ww be the weight of the suspended crate full of priceless art objects. The strut is uniform and also has weight w. Find the direction of the force exerted on the strut by the pivot in the arrangement (b). Express your answer in degrees.arrow_forwardA 70.0 cm, uniform, 40.0 N shelf is supported horizontally by two vertical wires attached to the sloping ceiling (Figure 1). A very small 20.0 N tool is placed on the shelf midway between the points where the wires are attached to it. Find the tension in the left-hand wire. Express your answer with the appropriate units.arrow_forward
- Find the total bind Mev. binding energy for 13 Carbon, 6C (atomic mass = 13.0033554)arrow_forwardWhat is the 27 energy absorbed in this endothermic Auclear reaction 2] Al + 'n → 27 Mg + ! H? (The atom mass of "Al is 26.981539u. and that of 11 Mg is 26.984341u) MeVarrow_forwardWhat is the energy released in this nuclear reaction 1 F + "', H-1 O+ He? 19 19 16 (The atomic mass of 1F is 18.998403 u, and that of 20 is 15.9949154) MeV.arrow_forward
- What is the energy released in this B+ nuclear reaction خالد 2½ Al w/ Mg + ie? (The atomic mass of 11 Al is 23.9999394 and that > of 12 Mg is 23.985041 u) MeV.arrow_forwardWhat is the energy released / absorbed in this nuclear reaction 14 N+ & He → » O + ! N? (The atomic mass of 14 N is 14.003074u. 17N+ and that of 10 is 16.9991324). MeVarrow_forwardCan someone help me answer this question thanks.arrow_forward
- Can someone help me with this question thanks.arrow_forward4B. Four electrons are located on the corners of a square, one on each corner, with the sides of the square being 25 cm long. a) Draw a sketch of the scenario and use your sketch to b) Determine the total force (magnitude and direction) on one of the electrons from the other three?arrow_forwardPortfolio Problem 3. A ball is thrown vertically upwards with a speed vo from the floor of a room of height h. It hits the ceiling and then returns to the floor, from which it rebounds, managing just to hit the ceiling a second time. Assume that the coefficient of restitution between the ball and the floor, e, is equal to that between the ball and the ceiling. Compute e.arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





