Chapter 11, Problem 11.4.4P

Solve the preceding problem for a steel pipe column (E = 210 GPa) with length L = 1.2 m, inner diameter d₂= 36 mm, and outer diameter d₂=40 mm.

  

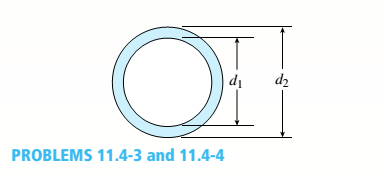
To determine

The critical load for the pinned-pinned end condition.

Answer to Problem 11.4.4P

The critical load for the pinned-pinned condition is 62.201 kN

Explanation of Solution

Given:

E=210 GPa

L= 1.2 m

d₁= 36 mm

d₂= 40 mm

Concept Used:

  $\begin{array}{l}Momentof\mathrm{int}eriaofthecolumn,I=\frac{\pi \left(d_0{}^4-d_i{}^4\right)}{64}\\ Thecriticalloadofthecolumn,P_{cr}=\frac{{\pi }^{2}EI}{L_{effective}{}^2}\\ Where,\\ I=momentofinertia\\ E=\mathrm{mod}ulusofelasticity\end{array}$

Calculation:

  $\begin{array}{l}Momentof\mathrm{int}eriaofthecolumn,I=\frac{\pi \left(d_0{}^4-d_i{}^4\right)}{64}\\ I=\frac{\pi \left({40}^4-{36}^4\right)}{64}\\ I=43215.75m{m}^4\\ Thecriticalloadofthecolumn,P_{cr}=\frac{{\pi }^{2}EI}{L_{effective}{}^2}\\ Forpinned-pinnedendcodition\text{}{L}_{effective}=L\\ P_{cr}=\frac{{\pi }^2\times 210\times {10}^3\times 43215.75}{{\left(1200\right)}^2}\\ P_{cr}=62.201kN\end{array}$

Conclusion:

The critical load for the pinned-pinned condition is 62.201 kN

To determine

The critical load for the fixed-free end condition.

Answer to Problem 11.4.4P

The critical load for the fixed-free end condition is 15.550 kN

Explanation of Solution

Given:

E=210 GPa

L= 1.2 m

d₁= 36 mm

d₂= 40 mm

Concept Used:

  $\begin{array}{l}Momentof\mathrm{int}eriaofthecolumn,I=\frac{\pi \left(d_0{}^4-d_i{}^4\right)}{64}\\ Thecriticalloadofthecolumn,P_{cr}=\frac{{\pi }^{2}EI}{L_{effective}{}^2}\\ Where,\\ I=momentofinertia\\ E=\mathrm{mod}ulusofelasticity\end{array}$

Calculation:

  $\begin{array}{l}Momentof\mathrm{int}eriaofthecolumn,I=\frac{\pi \left(d_0{}^4-d_i{}^4\right)}{64}\\ I=\frac{\pi \left({40}^4-{36}^4\right)}{64}\\ I=43215.75m{m}^4\\ Thecriticalloadofthecolumn,P_{cr}=\frac{{\pi }^{2}EI}{L_{effective}{}^2}\\ Forfixed-freeendcodition\text{}{L}_{effective}=2L\\ P_{cr}=\frac{{\pi }^2\times 210\times {10}^3\times 43215.75}{{\left(2\times 1200\right)}^2}\\ P_{cr}=15.550kN\end{array}$

Conclusion:

The critical load for the fixed-free end condition is 15.550 kN

To determine

The critical load for the fixed-pinned end condition.

Answer to Problem 11.4.4P

The critical load for the fixed-pinned end condition is 127.304 kN

Explanation of Solution

Given:

E=210 GPa

L= 1.2 m

d₁= 36 mm

d₂= 40 mm

Concept Used:

  $\begin{array}{l}Momentof\mathrm{int}eriaofthecolumn,I=\frac{\pi \left(d_0{}^4-d_i{}^4\right)}{64}\\ Thecriticalloadofthecolumn,P_{cr}=\frac{{\pi }^{2}EI}{L_{effective}{}^2}\\ Where,\\ I=momentofinertia\\ E=\mathrm{mod}ulusofelasticity\end{array}$

Calculation:

  $\begin{array}{l}Momentof\mathrm{int}eriaofthecolumn,I=\frac{\pi \left(d_0{}^4-d_i{}^4\right)}{64}\\ I=\frac{\pi \left({40}^4-{36}^4\right)}{64}\\ I=43215.75m{m}^4\\ Thecriticalloadofthecolumn,P_{cr}=\frac{{\pi }^{2}EI}{L_{effective}{}^2}\\ Forfixed-pinnedendcodition\text{}{L}_{effective}=0.699L\\ P_{cr}=\frac{{\pi }^2\times 210\times {10}^3\times 43215.75}{{\left(0.699\times 1200\right)}^2}\\ P_{cr}=127.304kN\end{array}$

Conclusion:

The critical load for the fixed-pinned end condition is 127.304 kN

To determine

The critical load for the fixed-fixed end condition.

Answer to Problem 11.4.4P

The critical load for the fixed-fixed end condition is 248.804 kN

Explanation of Solution

Given:

E=210 GPa

L= 1.2 m

d₁= 36 mm

d₂= 40 mm

Concept Used:

  $\begin{array}{l}Momentof\mathrm{int}eriaofthecolumn,I=\frac{\pi \left(d_0{}^4-d_i{}^4\right)}{64}\\ Thecriticalloadofthecolumn,P_{cr}=\frac{{\pi }^{2}EI}{L_{effective}{}^2}\\ Where,\\ I=momentofinertia\\ E=\mathrm{mod}ulusofelasticity\end{array}$

Calculation:

  $\begin{array}{l}Momentof\mathrm{int}eriaofthecolumn,I=\frac{\pi \left(d_0{}^4-d_i{}^4\right)}{64}\\ I=\frac{\pi \left({40}^4-{36}^4\right)}{64}\\ I=43215.75m{m}^4\\ Thecriticalloadofthecolumn,P_{cr}=\frac{{\pi }^{2}EI}{L_{effective}{}^2}\\ Forpinned-pinnedendcodition\text{}{L}_{effective}=\frac{L}{2}\\ P_{cr}=\frac{{\pi }^2\times 210\times {10}^3\times 43215.75*4}{{\left(1200\right)}^2}\\ P_{cr}=248.804kN\end{array}$

Conclusion:

The critical load for the fixed-fixed end condition is 248.804 kN