The Heart of Mathematics: An Invitation to Effective Thinking

4th Edition

ISBN: 9781118156599

Author: Edward B. Burger, Michael Starbird

Publisher: Wiley, John & Sons, Incorporated

See similar textbooks

Videos

Textbook Question

Chapter 10.5, Problem 23MS

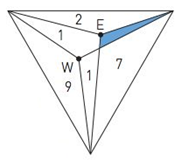
Barely consistent. It is possible for Chris to prefer the West piece if the cake is cut from the point marked W and the East piece if the cake is cut from the point marked E, even though the West piece is actually larger when cut from the point Ethanitis when cut from the point W. Suppose each pail of the cake has a value measured by the number written on the accompanying figure. What value could Chris view the shaded part of the cake as having in order to make the preference of East when the cake is cut from E consistent with the choice of West if the cake is cutfromW?

Chapter 10.5, Problem 23MS, Barely consistent. It is possible for Chris to prefer the West piece if the cake is cut from the

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 10.5, Problem 22MS

Chapter 10.5, Problem 28MS

Students have asked these similar questions

For context, the images attached below (the question and the related figure) is from a january 2024 past paper

For context, the image attached below is a question from a June 2024 past paper in statisical modeling

For context, the images attached below are a question from a June, 2024 past paper in statistical modeling

Chapter 10 Solutions

The Heart of Mathematics: An Invitation to Effective Thinking

Ch. 10.1 - What do you expect? How do you compute an expected...Ch. 10.1 - The average bite. Your little sister loves visits...Ch. 10.1 - A tooth for a tooth? Suppose your cousins Tooth...Ch. 10.1 - Spinning wheel. Suppose the spinner shown is...Ch. 10.1 - Fair game. What does it mean for a game to be...Ch. 10.1 - Cross on the green (S). A standard roulette wheel...Ch. 10.1 - In the red. Given the bet from Mindscape 6, what...Ch. 10.1 - Free Lotto. For several years in Massachusetts,...Ch. 10.1 - Bank value. What is the expected value of keeping...Ch. 10.1 - Value of money. In Newcombs Paradox, first suppose...

Ch. 10.1 - Die roll. What is the expected value of each of...Ch. 10.1 - Dice roll (ExH). What is the expected value of...Ch. 10.1 - Fair is foul. Someone has a weighted coin that...Ch. 10.1 - Foul is fair (S). Someone has a weighted coin that...Ch. 10.1 - Cycle cycle (H). You live in an area where the...Ch. 10.1 - Whats your pleasure? You have three options for...Ch. 10.1 - Roulette expectation. A standard roulette wheel...Ch. 10.1 - Fair wheeling. You are at the roulette table and...Ch. 10.1 - High rolling (H). Here is a die game you play...Ch. 10.1 - Fair rolling. Suppose you are considering the game...Ch. 10.1 - Spinning wheel. You pay $5, pick one of the four...Ch. 10.1 - Dice (ExH). You place a bet and then roll two fair...Ch. 10.1 - Uncoverable bases. Show by a specific example how...Ch. 10.1 - Under the cap. A national soda company runs a...Ch. 10.1 - Two coins in a fountain. You pay Si for two coins...Ch. 10.1 - Three coins in a fountain. You pay $5 for three...Ch. 10.1 - Insure (S). You own a $9000 car and a $850...Ch. 10.1 - Get a job (H). You search for a job. Three...Ch. 10.1 - Take this job and... Given the employment scenario...Ch. 10.1 - Book value. Refer back to our analysis of the...Ch. 10.1 - In search of... A group of deep-sea divers...Ch. 10.1 - Solid gold. There is a 50% chance that the price...Ch. 10.1 - Four out of five. In Newcombs Paradox, suppose...Ch. 10.1 - Chevalier de MĂ©rĂ©. Suppose that the Chevalier de...Ch. 10.1 - The St. Petersburg paradox. Here is an interesting...Ch. 10.1 - Coin or god. In Newcombs Paradox, first suppose...Ch. 10.1 - An investment. You wish to invest $1000, and you...Ch. 10.1 - Pap test (H). Assume that the insurance value of a...Ch. 10.1 - Prob. 40MS Ch. 10.1 - Spin to win. To play a certain carnival game, you...Ch. 10.1 - Spinner winner. To play a different carnival game,...Ch. 10.1 - Insurance wagering (H). From the point of view of...Ch. 10.1 - Probable cause. Continuing the scenario from the...Ch. 10.1 - The bicycle thief. Some entrepreneurial classmates...Ch. 10.2 - Remarkably risky. List two activities that are...Ch. 10.2 - Surprisinly safe. List two activities that are...Ch. 10.2 - Infectious numbers (H). Suppose a disease is...Ch. 10.2 - SARS scars (S). Suppose a new vaccine that...Ch. 10.2 - A hairy pot. At a certain famous school of...Ch. 10.2 - Blonde, bleached blonde (H). You have high...Ch. 10.2 - Blonde again (S). Given the scenario in Mindscape...Ch. 10.2 - Bleached again. Given the scenario in Mindscape 6,...Ch. 10.2 - Safety first. Suppose a particular car is widely...Ch. 10.2 - Scholarship winner (ExH). You apply for a national...Ch. 10.2 - Less safe (ExH). Given the scenario in our air...Ch. 10.2 - Aw, nuts! Suppose that the loss of life expectancy...Ch. 10.2 - Dont cell! (H) Suppose you are a U.S. senator and...Ch. 10.2 - Buy low and cell high (H). The microwaves produced...Ch. 10.2 - Taxi blues (H). An eyewitness observes a...Ch. 10.2 - More taxi blues (S). An eyewitness observes a...Ch. 10.2 - Few blues. An eyewitness observes a hit-and-run...Ch. 10.2 - More safety. Given the scenario of our earlier air...Ch. 10.2 - Reduced safety. Given the scenario of our air...Ch. 10.2 - HIV tests. Recall that, in the United States,...Ch. 10.2 - More HIV tests. Given the tests described in the...Ch. 10.2 - Super sale. The bookstore is having a super sale...Ch. 10.2 - V.isk risk (H). You always sort your laundry into...Ch. 10.2 - Bag for life. An insurance company estimates that...Ch. 10.2 - Mooving sale. Plush toy versions of your college...Ch. 10.2 - Reweighing life expectancy An example in this...Ch. 10.3 - Simple interest (H). Suppose you deposit $500 into...Ch. 10.3 - Less simple interest. Suppose that at the...Ch. 10.3 - The power of powers (H). In this section we...Ch. 10.3 - Crafty compounding. Two thousand years ago, a...Ch. 10.3 - Keg costs. List some of the opportunity costs...Ch. 10.3 - You can bank on us (or them) (S). You wish to...Ch. 10.3 - The Kennedy compound. You wish to ivest $1000 for...Ch. 10.3 - Three times a lady. The Three-Timesa-Year Savings...Ch. 10.3 - Baker kneads dough (ExH). Your favorite baker,...Ch. 10.3 - I want my ATV! You want to purchase a cool, yellow...Ch. 10.3 - Lottery loot later? You have a big problem: Youve...Ch. 10.3 - Open sesame (S). Bert and Ernie each open a...Ch. 10.3 - Jelly-filled investments (H). Suppose you purchase...Ch. 10.3 - Taking stock. Suppose that a stock transaction...Ch. 10.3 - Making your pocketbook stocky. Suppose that a...Ch. 10.3 - Money-tree house. You decide you wish to build...Ch. 10.3 - Future vlaue (S). What is the future value of $...Ch. 10.3 - Present value (ExH). On the first day of your...Ch. 10.3 - Double or nothing (H). You decide you wish to...Ch. 10.3 - Triple or nothing. You decide you wish to triple...Ch. 10.3 - Power versus product (S). In this section we...Ch. 10.3 - Double vision. Suppose we have $P and we invest it...Ch. 10.3 - Adding up the bucks (H). You have a job every...Ch. 10.3 - Fiddling for dollars. As presented in the section...Ch. 10.3 - Facebank. Your roommates are developing some...Ch. 10.3 - Boatload o cash. At age 12 you dream of sailing...Ch. 10.3 - Houseload o cash. You want to buy a house by age...Ch. 10.4 - Landslide Lyndon. The two candidates in the 1948...Ch. 10.4 - Electoral college. Briefly outline a voting scheme...Ch. 10.4 - Voting for voting. What are some differences...Ch. 10.4 - Voting for sport. Given an example (ideally from...Ch. 10.4 - The point of the arrow (S). What does Arrows...Ch. 10.4 - Dictating an election through a dictator. Suppose...Ch. 10.4 - Pro- or Con-dorcet? (S) Consider the following...Ch. 10.4 - Where is Dr. Pepper? (S) Given the voting data...Ch. 10.4 - Approval drinking (H). Returning to the voting...Ch. 10.4 - Mindscapes 10 through 15 are based on the...Ch. 10.4 - Mindscapes 10 through 15 are based on the...Ch. 10.4 - Mindscapes 10 through 15 are based on the...Ch. 10.4 - Mindscapes 10 through 15 are based on the...Ch. 10.4 - Mindscapes 10 through 15 are based on the...Ch. 10.4 - Mindscapes 10 through 15 are based on the...Ch. 10.4 - Whats it all about, Ralphie? Many people believe...Ch. 10.4 - Two, too (ExH). Given an election between just two...Ch. 10.4 - Two, too II (ExH). Given an election between just...Ch. 10.4 - Instant runoffs. One way to avoid the lengthy...Ch. 10.4 - Run runoff. Given the method of instant runoff...Ch. 10.4 - Coin coupling. For this challenge, you will need...Ch. 10.4 - From money-mating to cupids arrow. Explain how the...Ch. 10.4 - Vote night. There are four candidates running for...Ch. 10.4 - Wroof recount. The election in the previous...Ch. 10.4 - Biggest loser? Who was the biggest loser in the...Ch. 10.4 - The X-act winner. Your schools math club has 73...Ch. 10.4 - Borda rules. Candidates A, B, and C are running...Ch. 10.5 - Prob. 1MS Ch. 10.5 - Understanding icing (S). Suppose a person who had...Ch. 10.5 - Liquid gold. Suppose you and your two brothers are...Ch. 10.5 - East means West. Suppose you have a triangular...Ch. 10.5 - Two-bedroom bliss (H). Suppose you and a roommate...Ch. 10.5 - Your preference. Suppose the accompanying figure...Ch. 10.5 - Bulk. Suppose for you, bigger is better, so your...Ch. 10.5 - Dont move that knif. Give a specific scenario to...Ch. 10.5 - Prob. 9MS Ch. 10.5 - Just do it. Get three people together and have...Ch. 10.5 - The real world. Give three real-world examples...Ch. 10.5 - Same tastes (H). If you are dividing a cake among...Ch. 10.5 - Crossing the line. In each triangle shown on the...Ch. 10.5 - Cutting up Mass (S). You, Joan, and John want to...Ch. 10.5 - Where to cut (H). The accompanying figure pictures...Ch. 10.5 - Land preference (ExH). Suppose you are preparing...Ch. 10.5 - Uneven pair (S). Suppose two people want to divide...Ch. 10.5 - Diversity pays. Explain why having differences of...Ch. 10.5 - Be fair. The moving-knife and yelling Stop method...Ch. 10.5 - Nuclear dump (ExH). Suppose there is a nuclear...Ch. 10.5 - Disarming (H). Two nuclear superpowers decide to...Ch. 10.5 - Cupcakes. Suppose you had 100 different cupcakes...Ch. 10.5 - Barely consistent. It is possible for Chris to...Ch. 10.5 - Your X. You and your ex-roommate happen to share a...Ch. 10.5 - Musical Xs. You play the violin in a chamber trio...Ch. 10.5 - Cake plot. Imagine a cake in the shape of a...Ch. 10.5 - Cake trisection. Imagine a cake in the shape of a...Ch. 10.5 - Roomate wrangling. You and a friend rent a...

Additional Math Textbook Solutions

Find more solutions based on key concepts

The equivalent expression of x(y+z) by using the commutative property.

Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)

Testing Claims About Proportions. In Exercises 7–22, test the given claim. Identify the null hypothesis, altern...

Elementary Statistics (13th Edition)

Fill in each blank so that the resulting statement is true. If n is a counting number, bn, read ______, indicat...

College Algebra (7th Edition)

The length of the tarp on each side

Pre-Algebra Student Edition

Trigonometric limits Use Theorem 3.11 to evaluate the following limits. 12. lim0cos21

Calculus: Early Transcendentals (2nd Edition)

In Problems 13-20, a linear function is given. a. Determine the slope and y-intercept of each Junction. b. Use ...

Precalculus

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.