Chapter 10, Problem 10.4.9P

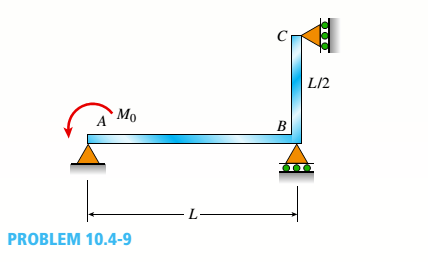
The continuous frame ABC has a pin support at A, roller supports at B and C and a rigid corner connection at B (see figure). Members AB and BC each have flexural rigidity EI. A moment M_üacts counterclockwise at A. Note: Disregard axial deformations in member AB and consider only the effects of bending.

1. Find all reactions of the frame.

Find joint rotations 6 at A, B, and C.

Find the required new length of member AB in terms of L, so that ${\theta }_A$

in part (b) is doubled in size.

  

To determine

All the reactions of the frame.

Answer to Problem 10.4.9P

The reactions are : $R_A=-R_B=4M_0/3L,H_A=-R_C=-2M_0/3L.$

Explanation of Solution

Given Information:

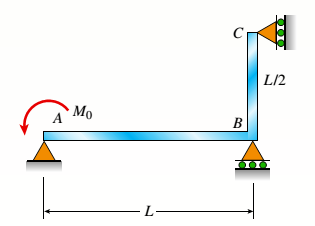
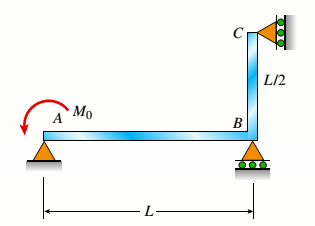
The following figure is given with all relevant information,

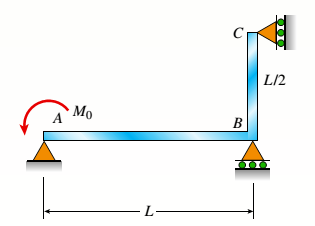
Calculation:

Consider the following free body diagram,

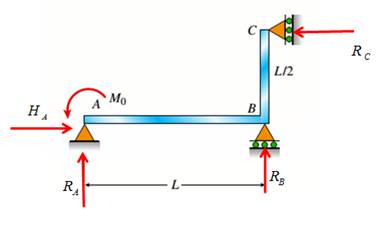
Take equilibrium of horizontal forces as,

$\begin{array}{l}{\displaystyle \sum F_H}=0\\ \Rightarrow H_A-R_C=0\mathrm{....}\text{(1)}\end{array}$

Take equilibrium of vertical forces as,

$\begin{array}{l}{\displaystyle \sum F_V}=0\\ \Rightarrow R_A+R_B=0\mathrm{....}\text{(2)}\end{array}$

Take equilibrium of moments about B as,

$\begin{array}{l}{\displaystyle \sum M_B}=0\\ \Rightarrow -R_{A}L+M_0+R_{C}L/2=0\mathrm{....}\text{(3)}\end{array}$

The bending moment at distance x from A along AB in part AB is given by,

$M_{AB}=R_{A}x-M_0$

Use second order deflection differential equation,

$\begin{array}{l}\frac{d^{2}v}{d{x}^2}=\frac{M}{EI}=\frac{M_{AB}}{EI}\\ \Rightarrow \frac{d^{2}v}{d{x}^2}=\frac{1}{EI}(R_{A}x-M_0)\end{array}$

Integrate above equation to get rotation as,

$\frac{dv}{dx}={\theta }_{AB}=\frac{1}{EI}(R_A{x}^2/2-M_{0}x+C_1)$

Integrate above equation to get rotation as,

$v={\delta }_{AB}=\frac{1}{EI}(R_A{x}^3/6-M_0{x}^2/2+C_{1}x+C_2)$

The bending moment at distance x from B along BC in part BC is given by,

$M_{BC}=R_{C}L/2-R_{C}x$

Use second order deflection differential equation,

  $\begin{array}{l}\frac{d^{2}v}{d{x}^2}=\frac{M}{EI}=\frac{M_{BC}}{EI}\\ \Rightarrow \frac{d^{2}v}{d{x}^2}=\frac{1}{EI}(R_{C}L/2-R_{C}x)\end{array}$

Integrate above equation to get rotation as,

$\frac{dv}{dx}={\theta }_{BC}=\frac{1}{EI}(R_{C}Lx/2-R_C{x}^2/2+C_3)$

Integrate above equation to get rotation as,

$v={\delta }_{BC}=\frac{1}{EI}(R_{C}L{x}^2/4-R_C{x}^3/6+C_{3}x+C_4)$

The constraint equations are,

$\begin{array}{l}{\delta }_{AB}(0)=0\mathrm{...}\text{(4)}\\ {\delta }_{AB}(L)=0\mathrm{...}\text{(5)}\\ {\delta }_{BC}(0)=0\mathrm{...}\text{(6)}\\ {\delta }_{BC}(L/2)=0\mathrm{..}\text{(7)}\\ {\theta }_{AB}(L)={\theta }_{BC}\text{(0) }\mathrm{..}\text{(8)}\end{array}$

Solve equations (1-8) to get integration constants and reactions.

So the reactions are $R_A=-R_B=4M_0/3L,H_A=-R_C=-2M_0/3L.$

Conclusion:

Therefore, the reactions are: $R_A=-R_B=4M_0/3L,H_A=-R_C=-2M_0/3L.$

To determine

Rotations at joints A, B, and C.

Answer to Problem 10.4.9P

Rotations at joints A, B, and C are ${\theta }_A=\frac{5M_{0}L}{18EI},{\theta }_B=\frac{-M_{0}L}{18EI},{\theta }_C=\frac{M_{0}L}{36EI}\text{. }$

Explanation of Solution

Given Information:

The following figure is given with all relevant information,

Calculation:

Consider the following free body diagram,

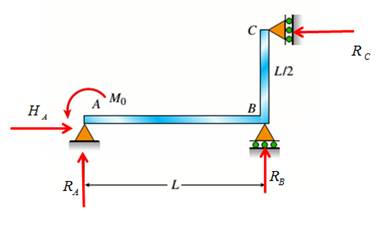
Take equilibrium of horizontal forces as,

$\begin{array}{l}{\displaystyle \sum F_H}=0\\ \Rightarrow H_A-R_C=0\mathrm{....}\text{(1)}\end{array}$

Take equilibrium of vertical forces as,

$\begin{array}{l}{\displaystyle \sum F_V}=0\\ \Rightarrow R_A+R_B=0\mathrm{....}\text{(2)}\end{array}$

Take equilibrium of moments about B as,

$\begin{array}{l}{\displaystyle \sum M_B}=0\\ \Rightarrow -R_{A}L+M_0+R_{C}L/2=0\mathrm{....}\text{(3)}\end{array}$

The bending moment at distance x from A along AB in part AB is given by,

$M_{AB}=R_{A}x-M_0$

Use second order deflection differential equation,

$\begin{array}{l}\frac{d^{2}v}{d{x}^2}=\frac{M}{EI}=\frac{M_{AB}}{EI}\\ \Rightarrow \frac{d^{2}v}{d{x}^2}=\frac{1}{EI}(R_{A}x-M_0)\end{array}$

Integrate above equation to get rotation as,

$\frac{dv}{dx}={\theta }_{AB}=\frac{1}{EI}(R_A{x}^2/2-M_{0}x+C_1)$

Integrate above equation to get rotation as,

$v={\delta }_{AB}=\frac{1}{EI}(R_A{x}^3/6-M_0{x}^2/2+C_{1}x+C_2)$

The bending moment at distance x from B along BC in part BC is given by,

$M_{BC}=R_{C}L/2-R_{C}x$

Use second order deflection differential equation,

  $\begin{array}{l}\frac{d^{2}v}{d{x}^2}=\frac{M}{EI}=\frac{M_{BC}}{EI}\\ \Rightarrow \frac{d^{2}v}{d{x}^2}=\frac{1}{EI}(R_{C}L/2-R_{C}x)\end{array}$

Integrate above equation to get rotation as,

$\frac{dv}{dx}={\theta }_{BC}=\frac{1}{EI}(R_{C}Lx/2-R_C{x}^2/2+C_3)$

Integrate above equation to get rotation as,

$v={\delta }_{BC}=\frac{1}{EI}(R_{C}L{x}^2/4-R_C{x}^3/6+C_{3}x+C_4)$

The constraint equations are,

$\begin{array}{l}{\delta }_{AB}(0)=0\mathrm{...}\text{(4)}\\ {\delta }_{AB}(L)=0\mathrm{...}\text{(5)}\\ {\delta }_{BC}(0)=0\mathrm{...}\text{(6)}\\ {\delta }_{BC}(L/2)=0\mathrm{..}\text{(7)}\\ {\theta }_{AB}(L)={\theta }_{BC}\text{(0) }\mathrm{..}\text{(8)}\end{array}$

Solve equations (1-8) to get integration constants and reactions.

So the reactions are $R_A=-R_B=4M_0/3L,H_A=-R_C=-2M_0/3L.$

Substitute the integration constants and reactions in expressions of rotations to get,

$\begin{array}{l}{\theta }_{AB}(0)={\theta }_A=\frac{5M_{0}L}{18EI},\\ {\theta }_{AB}(L)={\theta }_B=\frac{-M_{0}L}{18EI},\\ {\theta }_{BC}(L/2)={\theta }_C=\frac{M_{0}L}{36EI}\text{. }\end{array}$

Conclusion:

Therefore, rotations at joints A, B, and C are ${\theta }_A=\frac{5M_{0}L}{18EI},{\theta }_B=\frac{-M_{0}L}{18EI},{\theta }_C=\frac{M_{0}L}{36EI}\text{. }$

To determine

Length of AB.

Answer to Problem 10.4.9P

Length of AB is $L_{AB}=2.088L$.

Explanation of Solution

Given Information:

The following figure is given with all relevant information,

Also ${\theta }_A=\frac{5M_{0}L}{9EI}$ .

Calculation:

Consider the following free body diagram,

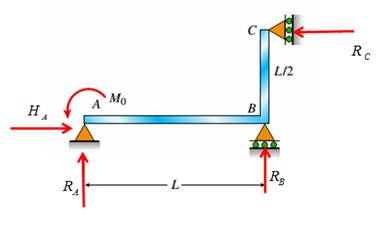
Take equilibrium of horizontal forces as,

$\begin{array}{l}{\displaystyle \sum F_H}=0\\ \Rightarrow H_A-R_C=0\mathrm{....}\text{(1)}\end{array}$

Take equilibrium of vertical forces as,

$\begin{array}{l}{\displaystyle \sum F_V}=0\\ \Rightarrow R_A+R_B=0\mathrm{....}\text{(2)}\end{array}$

Take equilibrium of moments about B as,

$\begin{array}{l}{\displaystyle \sum M_B}=0\\ \Rightarrow -R_{A}L+M_0+R_{C}L/2=0\mathrm{....}\text{(3)}\end{array}$

The bending moment at distance x from A along AB in part AB is given by,

$M_{AB}=R_{A}x-M_0$

Use second order deflection differential equation,

$\begin{array}{l}\frac{d^{2}v}{d{x}^2}=\frac{M}{EI}=\frac{M_{AB}}{EI}\\ \Rightarrow \frac{d^{2}v}{d{x}^2}=\frac{1}{EI}(R_{A}x-M_0)\end{array}$

Integrate above equation to get rotation as,

$\frac{dv}{dx}={\theta }_{AB}=\frac{1}{EI}(R_A{x}^2/2-M_{0}x+C_1)$

Integrate above equation to get rotation as,

$v={\delta }_{AB}=\frac{1}{EI}(R_A{x}^3/6-M_0{x}^2/2+C_{1}x+C_2)$

The bending moment at distance x from B along BC in part BC is given by,

$M_{BC}=R_{C}L/2-R_{C}x$

Use second order deflection differential equation,

  $\begin{array}{l}\frac{d^{2}v}{d{x}^2}=\frac{M}{EI}=\frac{M_{BC}}{EI}\\ \Rightarrow \frac{d^{2}v}{d{x}^2}=\frac{1}{EI}(R_{C}L/2-R_{C}x)\end{array}$

Integrate above equation to get rotation as,

$\frac{dv}{dx}={\theta }_{BC}=\frac{1}{EI}(R_{C}Lx/2-R_C{x}^2/2+C_3)$

Integrate above equation to get rotation as,

$v={\delta }_{BC}=\frac{1}{EI}(R_{C}L{x}^2/4-R_C{x}^3/6+C_{3}x+C_4)$

The constraint equations are,

$\begin{array}{l}{\delta }_{AB}(0)=0\mathrm{...}\text{(4)}\\ {\delta }_{AB}(L)=0\mathrm{...}\text{(5)}\\ {\delta }_{BC}(0)=0\mathrm{...}\text{(6)}\\ {\delta }_{BC}(L/2)=0\mathrm{..}\text{(7)}\\ {\theta }_{AB}(L)={\theta }_{BC}\text{(0) }\mathrm{..}\text{(8)}\end{array}$

Solve equations (1-8) to get integration constants and reactions.

So the reactions are $R_A=-R_B=4M_0/3L,H_A=-R_C=-2M_0/3L.$

Substitute the integration constants and reactions in expressions of rotations to get,

${\theta }_{AB}(L_{AB})={\theta }_A=\frac{5M_{0}L}{9EI}$

Solve above equation to get $L_{AB}=2.088L$ .

Conclusion:

Therefore, length of AB is $L_{AB}=2.088L$ .