Chapter 10, Problem 10.31P

To determine

(a)

The values of gain $K_P\text{and}{K}_I$ of the PI controller of first-order plant for the following cases:

Case 1. For $\zeta =0.707$.

Case 2. For $\zeta =1$.

Case 3. For a root separation factor of 5.

Answer to Problem 10.31P

The values of gains for the PI controller are as follows:

Case 1. For $\zeta =0.707$, $K_I=5$ and $K_P=5$.

Case 2. For $\zeta =1$, $K_I=2.5$ and $K_P=5$.

Case 3. For a root separation factor of 5, $K_I=12.5$ and $K_P=25$.

Explanation of Solution

Given:

The proportional integral controller of first order plant is as shown below:

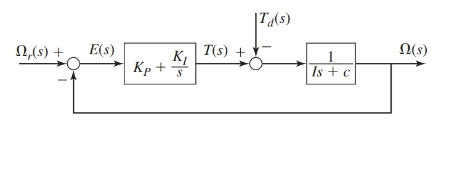
Where, the parameter values are as given:

$I=10,c=5$

Also, the performance specifications require the time constant of the system to be $\tau =2$.

Concept Used:

1. The transfer functions for the block diagram are as shown below:

$\begin{array}{l}\frac{\Omega \left(s\right)}{{\Omega }_r\left(s\right)}=\frac{s{K}_P+K_I}{I{s}^2+s\left(c+K_P\right)+K_I}\\ \frac{\Omega \left(s\right)}{T_d\left(s\right)}=\frac{-s}{I{s}^2+s\left(c+K_P\right)+K_I}\end{array}$

For a second order system having a characteristic equation of the form $s^2+2\zeta {\omega }_{n}s+{\omega }_n{}^2=0$, the characteristic roots are of the form $s=-\zeta {\omega }_{n}s\pm {\omega }_n\sqrt{1-{\zeta }^2}\forall \zeta \le 1$ .

Also, the corresponding time constant for the system would be $\tau =\frac{1}{\zeta {\omega }_n}$.

2. For a second order system, if the root separation factor is K then, we have following conclusions for the roots and their corresponding time constant, that is
For roots $s_1\text{and}{s}_2$ ,

$\frac{s_1}{s_2}=K$

The corresponding time constants of the system would be:

$\frac{{\tau }_1}{{\tau }_2}=\frac{\frac{1}{\mathrm{Re}\left(s_1\right)}}{\frac{1}{\mathrm{Re}\left(s_2\right)}}=\frac{\mathrm{Re}\left(s_2\right)}{\mathrm{Re}\left(s_1\right)}=\frac{1}{K}$

Calculation:

From the block diagram as shown, the transfer functions are as:

$\begin{array}{l}\frac{\Omega \left(s\right)}{{\Omega }_r\left(s\right)}=\frac{s{K}_P+K_I}{I{s}^2+s\left(c+K_P\right)+K_I}\\ \frac{\Omega \left(s\right)}{T_d\left(s\right)}=\frac{-s}{I{s}^2+s\left(c+K_P\right)+K_I}\end{array}$

Therefore, the characteristic equation for the system is:

$I{s}^2+s\left(c+K_P\right)+K_I=0$

On putting the values of parameters in this expression of characteristic equation:

$\begin{array}{l}I{s}^2+s\left(c+K_P\right)+K_I=0\\ \Rightarrow 10s^2+s\left(5+K_P\right)+K_I=0\because I=10,c=5\\ \Rightarrow s^2+s\frac{\left(5+K_P\right)}{10}+\frac{K_I}{10}=0\end{array}$

On comparing this equation with form $s^2+2\zeta {\omega }_{n}s+{\omega }_n{}^2=0$, we get

Undamped natural frequency:

$\begin{array}{l}{\omega }_n{}^2=\frac{K_I}{10}\\ \Rightarrow {\omega }_n=\sqrt{\frac{K_I}{10}}\text{rad/sec}\end{array}$

Damping ratio:

$\begin{array}{l}2\zeta {\omega }_n=\frac{\left(5+K_P\right)}{10}\\ \Rightarrow \zeta =\frac{\left(5+K_P\right)}{20{\omega }_n}\\ \Rightarrow \zeta =\frac{\left(5+K_P\right)}{20\sqrt{\frac{K_I}{10}}}\\ \Rightarrow \zeta =\frac{\left(5+K_P\right)}{2\cdot \sqrt{10K_I}}\end{array}$

Thus, the time constant for the system is:

$\begin{array}{l}\tau =\frac{1}{\zeta {\omega }_n}\\ \Rightarrow \tau =\frac{1}{\frac{\left(5+K_P\right)}{2\cdot \sqrt{10K_I}}\cdot \sqrt{\frac{K_I}{10}}}\because \zeta =\frac{\left(5+K_P\right)}{2\cdot \sqrt{10K_I}},{\omega }_n=\sqrt{\frac{K_I}{10}}\text{rad/sec}\\ \Rightarrow \tau =\frac{20}{\left(5+K_P\right)}\end{array}$

As the performance specifications require the time constant of the system to be $\tau =2$.

Therefore, at $\tau =2$

$\begin{array}{l}\tau =\frac{20}{\left(5+K_P\right)}\\ \Rightarrow 2=\frac{20}{\left(5+K_P\right)}\\ \Rightarrow 5+K_P=10\\ \Rightarrow K_P=5\end{array}$

Case 1. When $\zeta =0.707$, the gain value of $K_I$ is:

Since, $\zeta =\frac{\left(5+K_P\right)}{2\cdot \sqrt{10K_I}}$

$\begin{array}{l}\Rightarrow 0.707=\frac{\left(5+K_P\right)}{2\cdot \sqrt{10K_I}}\because K_P=5\\ \Rightarrow 1.414\sqrt{10K_I}=10\\ \Rightarrow \sqrt{K_I}=\frac{\sqrt{10}}{1.414}=2.24\\ \Rightarrow K_I=5.01\approx 5\end{array}$

Case 2. When $\zeta =1$, the gain value of $K_I$ is:

Since, $\zeta =\frac{\left(5+K_P\right)}{2\cdot \sqrt{10K_I}}$

$\begin{array}{l}\Rightarrow 1=\frac{\left(5+K_P\right)}{2\cdot \sqrt{10K_I}}\because K_P=5\\ \Rightarrow \sqrt{K_I}=\frac{10}{2\sqrt{10}}\\ \Rightarrow K_I=2.5\end{array}$

Case 3. When the root separation factor is 5.

For this value of the root separation factor $\frac{s_1}{s_2}=5$, the ratio of time constants for the roots would be:

$\frac{{\tau }_1}{{\tau }_2}=\frac{1}{5}$

As given in the question system, performance requires time constant to be 2seconds or say the dominant time constant to be 2 seconds then the secondary time constant would be 0.4 seconds. Therefore, the characteristic roots corresponding to these time constants would be:

$s=-\frac{1}{2}=-0.5,s=-\frac{1}{0.4}=-2.5$

Thus, the corresponding characteristic equation for the system will be:

$\begin{array}{l}s=-0.5,s=-2.5\\ \Rightarrow \left(s+0.5\right)\left(s+2.5\right)=0\\ \Rightarrow s^2+3s+1.25=0\end{array}$

On comparing this equation with $s^2+s\frac{\left(5+K_P\right)}{10}+\frac{K_I}{10}=0$, we get

$\begin{array}{l}\frac{K_I}{10}=1.25\\ \Rightarrow K_I=12.5\end{array}$

And

$\begin{array}{l}\frac{\left(5+K_P\right)}{10}=3\\ \Rightarrow 5+K_P=30\\ \Rightarrow K_P=25\end{array}$.

Conclusion:

The values of gains for the PI controller areas follows:

Case 1. For $\zeta =0.707$, $K_I=5$ and $K_P=5$.

Case 2. For $\zeta =1$, $K_I=2.5$ and $K_P=5$.

Case 3. For a root separation factor of 5, $K_I=12.5$ and $K_P=25$.

To determine

(b)

To plot:

The response $\Omega \left(s\right)$ for the unit-step command response ${\Omega }_r\left(s\right)$ for all the cases in sub-part (a)

Also, compare the responses obtained in all these cases.

Answer to Problem 10.31P

The response $\Omega \left(s\right)$ for the unit-step command response ${\Omega }_r\left(s\right)$ for all the cases in sub-part (a) is shown in Figure 1. At the damping ratio, $\zeta =0.707$, there is a small overshoot encountered in the response while for the cases where damping ratios are 1 and 1.34 respectively shows the overdamping in the response. And the responses in the first and second case are sluggish, while the response for the third case is faster with the less settling time.

Explanation of Solution

Given:

The proportional integral controller of first order plant is as shown below:

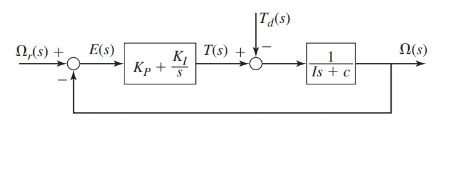
Where, the parameter values are as given:

$I=10,c=5$

Also, the performance specifications require the time constant of the system to be $\tau =2$.

The values of gains for the PI controller are as follows:

Case 1. For $\zeta =0.707$, $K_I=5$ and $K_P=5$.

Case 2. For $\zeta =1$, $K_I=2.5$ and $K_P=5$.

Case 3. For a root separation factor of 5, $K_I=12.5$ and $K_P=25$.

Concept Used:

1. The transfer functions for the block diagram are as shown below:

$\begin{array}{l}\frac{\Omega \left(s\right)}{{\Omega }_r\left(s\right)}=\frac{s{K}_P+K_I}{I{s}^2+s\left(c+K_P\right)+K_I}\\ \frac{\Omega \left(s\right)}{T_d\left(s\right)}=\frac{-s}{I{s}^2+s\left(c+K_P\right)+K_I}\end{array}$.

Calculation:

From the block diagram as shown, the transfer functions are as:

$\begin{array}{l}\frac{\Omega \left(s\right)}{{\Omega }_r\left(s\right)}=\frac{s{K}_P+K_I}{I{s}^2+s\left(c+K_P\right)+K_I}\\ \frac{\Omega \left(s\right)}{T_d\left(s\right)}=\frac{-s}{I{s}^2+s\left(c+K_P\right)+K_I}\end{array}$

Therefore, the response $\Omega \left(s\right)$ for the system is:

$\Omega \left(s\right)=\frac{s{K}_P+K_I}{I{s}^2+s\left(c+K_P\right)+K_I}{\Omega }_r\left(s\right)-\frac{s}{I{s}^2+s\left(c+K_P\right)+K_I}{T}_d\left(s\right)$

On putting the values of parameters in this expression of characteristic equation:

$\begin{array}{l}\Omega \left(s\right)=\frac{s{K}_P+K_I}{I{s}^2+s\left(c+K_P\right)+K_I}{\Omega }_r\left(s\right)-\frac{s}{I{s}^2+s\left(c+K_P\right)+K_I}{T}_d\left(s\right)\\ \because I=10,c=5\\ \Rightarrow \Omega \left(s\right)=\frac{s{K}_P+K_I}{10s^2+s\left(5+K_P\right)+K_I}{\Omega }_r\left(s\right)-\frac{s}{10s^2+s\left(5+K_P\right)+K_I}{T}_d\left(s\right)\end{array}$

Case 1. When $\zeta =0.707$, the gain values are $K_I=5$ and $K_P=5$:

Since, $\Omega \left(s\right)=\frac{s{K}_P+K_I}{10s^2+s\left(5+K_P\right)+K_I}{\Omega }_r\left(s\right)-\frac{s}{10s^2+s\left(5+K_P\right)+K_I}{T}_d\left(s\right)$

$\begin{array}{l}\Rightarrow \Omega \left(s\right)=\frac{5s+5}{10s^2+s\left(5+5\right)+5}{\Omega }_r\left(s\right)-\frac{s}{10s^2+s\left(5+5\right)+5}{T}_d\left(s\right)\\ \because K_P=5,K_I=5\\ \Rightarrow \Omega \left(s\right)=\frac{5s+5}{10s^2+10s+5}{\Omega }_r\left(s\right)-\frac{s}{10s^2+10s+5}{T}_d\left(s\right)\end{array}$

Therefore, for unit-step command response ${\Omega }_r\left(s\right)$ and zero disturbance torque $T_d\left(s\right)$, we have

$\begin{array}{l}\Omega \left(s\right)=\frac{5s+5}{10s^2+10s+5}{\Omega }_r\left(s\right)-\frac{s}{10s^2+10s+5}{T}_d\left(s\right)\\ \Rightarrow \Omega \left(s\right)=\frac{5s+5}{10s^2+10s+5}\cdot \frac{1}{s}-\frac{s}{10s^2+10s+5}\cdot 0\\ \Rightarrow \Omega \left(s\right)=\frac{5s+5}{10s^2+10s+5}\cdot \frac{1}{s}\end{array}$

On simplifying this response of $\Omega \left(s\right)$ using partial fraction expansion, we get

$\begin{array}{l}\Omega \left(s\right)=\frac{5s+5}{10s^2+10s+5}\cdot \frac{1}{s}=\frac{s+1}{2s^2+2s+1}\cdot \frac{1}{s}\\ \Rightarrow \Omega \left(s\right)=\frac{1}{s}-\frac{\left(2s+1\right)}{2s^2+2s+1}\end{array}$

On taking inverse Laplace transform of this, we have

$\begin{array}{l}\Omega \left(s\right)=\frac{1}{s}-\frac{\left(2s+1\right)}{2s^2+2s+1}=\frac{1}{s}-\frac{\left(s+\frac{1}{2}\right)}{s^2+s+\frac{1}{2}}=\frac{1}{s}-\frac{\left(s+\frac{1}{2}\right)}{{\left(s+\frac{1}{2}\right)}^2+{\left(\frac{1}{2}\right)}^2}\\ \Rightarrow \omega \left(t\right)=1-e^{-\frac{1}{2}t}\cos \left(\frac{1}{2}t\right)\end{array}$

Case 2. When $\zeta =1$, the gain values are $K_I=2.5$ and $K_P=5$:

Since, $\Omega \left(s\right)=\frac{s{K}_P+K_I}{10s^2+s\left(5+K_P\right)+K_I}{\Omega }_r\left(s\right)-\frac{s}{10s^2+s\left(5+K_P\right)+K_I}{T}_d\left(s\right)$

$\begin{array}{l}\Rightarrow \Omega \left(s\right)=\frac{5s+2.5}{10s^2+s\left(5+5\right)+2.5}{\Omega }_r\left(s\right)-\frac{s}{10s^2+s\left(5+5\right)+2.5}{T}_d\left(s\right)\\ \because K_P=5,K_I=2.5\end{array}$

$\Rightarrow \Omega \left(s\right)=\frac{5s+2.5}{10s^2+10s+2.5}{\Omega }_r\left(s\right)-\frac{s}{10s^2+10s+2.5}{T}_d\left(s\right)$

Therefore, for unit-step command response ${\Omega }_r\left(s\right)$ and zero disturbance torque $T_d\left(s\right)$, we have

$\begin{array}{l}\Omega \left(s\right)=\frac{5s+2.5}{10s^2+10s+2.5}{\Omega }_r\left(s\right)-\frac{s}{10s^2+10s+2.5}{T}_d\left(s\right)\\ \Rightarrow \Omega \left(s\right)=\frac{5s+2.5}{10s^2+10s+2.5}\cdot \frac{1}{s}-\frac{s}{10s^2+10s+2.5}\cdot 0\\ \Rightarrow \Omega \left(s\right)=\frac{5s+2.5}{10s^2+10s+2.5}\cdot \frac{1}{s}\end{array}$

On simplifying this response of $\Omega \left(s\right)$ using partial fraction expansion, we get

$\begin{array}{l}\Omega \left(s\right)=\frac{5s+2.5}{10s^2+10s+2.5}\cdot \frac{1}{s}\\ \Rightarrow \Omega \left(s\right)=\frac{1}{s}-\frac{10s+5}{10s^2+10s+2.5}\end{array}$

On taking inverse Laplace transform of this, we have

$\begin{array}{l}\Omega \left(s\right)=\frac{1}{s}-\frac{10s+5}{10s^2+10s+2.5}=\frac{1}{s}-\frac{\left(s+\frac{1}{2}\right)}{s^2+s+\frac{1}{4}}=\frac{1}{s}-\frac{\left(s+\frac{1}{2}\right)}{{\left(s+\frac{1}{2}\right)}^2}\\ \Rightarrow \Omega \left(s\right)=\frac{1}{s}-\frac{1}{\left(s+\frac{1}{2}\right)}\\ \Rightarrow \omega \left(t\right)=1-e^{-\frac{1}{2}t}\end{array}$

Case 3. When the root separation factor is 5.

That is, the gain values are $K_I=12.5$ and $K_P=25$:

Since, $\Omega \left(s\right)=\frac{s{K}_P+K_I}{10s^2+s\left(5+K_P\right)+K_I}{\Omega }_r\left(s\right)-\frac{s}{10s^2+s\left(5+K_P\right)+K_I}{T}_d\left(s\right)$

$\begin{array}{l}\Rightarrow \Omega \left(s\right)=\frac{25s+12.5}{10s^2+s\left(5+25\right)+12.5}{\Omega }_r\left(s\right)-\frac{s}{10s^2+s\left(5+25\right)+12.5}{T}_d\left(s\right)\\ \because K_P=25,K_I=12.5\end{array}$

$\Rightarrow \Omega \left(s\right)=\frac{25s+12.5}{10s^2+30s+12.5}{\Omega }_r\left(s\right)-\frac{s}{10s^2+30s+12.5}{T}_d\left(s\right)$

Therefore, for unit-step command response ${\Omega }_r\left(s\right)$ and zero disturbance torque $T_d\left(s\right)$, we have

$\begin{array}{l}\Omega \left(s\right)=\frac{25s+12.5}{10s^2+30s+12.5}{\Omega }_r\left(s\right)-\frac{s}{10s^2+30s+12.5}{T}_d\left(s\right)\\ \Rightarrow \Omega \left(s\right)=\frac{25s+12.5}{10s^2+30s+12.5}\cdot \frac{1}{s}-\frac{s}{10s^2+30s+12.5}\cdot 0\\ \Rightarrow \Omega \left(s\right)=\frac{25s+12.5}{10s^2+30s+12.5}\cdot \frac{1}{s}\end{array}$

On simplifying this response of $\Omega \left(s\right)$ using partial fraction expansion, we get

$\begin{array}{l}\Omega \left(s\right)=\frac{25s+12.5}{10s^2+30s+12.5}\cdot \frac{1}{s}\\ \Rightarrow \Omega \left(s\right)=\frac{1}{s}-\frac{10s+5}{10s^2+30s+12.5}\end{array}$

On taking inverse Laplace transform of this, we have

$\begin{array}{l}\Omega \left(s\right)=\frac{1}{s}-\frac{10s+5}{10s^2+30s+12.5}=\frac{1}{s}-\frac{\left(s+\frac{1}{2}\right)}{s^2+3s+1.25}\\ \Rightarrow \Omega \left(s\right)=\frac{1}{s}-\frac{\left(s+\frac{3}{2}\right)}{{\left(s+\frac{3}{2}\right)}^2-{\left(1\right)}^2}+\frac{1}{{\left(s+\frac{3}{2}\right)}^2-{\left(1\right)}^2}\\ \Rightarrow \omega \left(t\right)=1-e^{-\frac{3}{2}t}\cosh \left(t\right)+e^{-\frac{3}{2}t}\sinh \left(t\right)\end{array}$

On plotting the responses $\omega \left(t\right)$ for all the three cases, we have

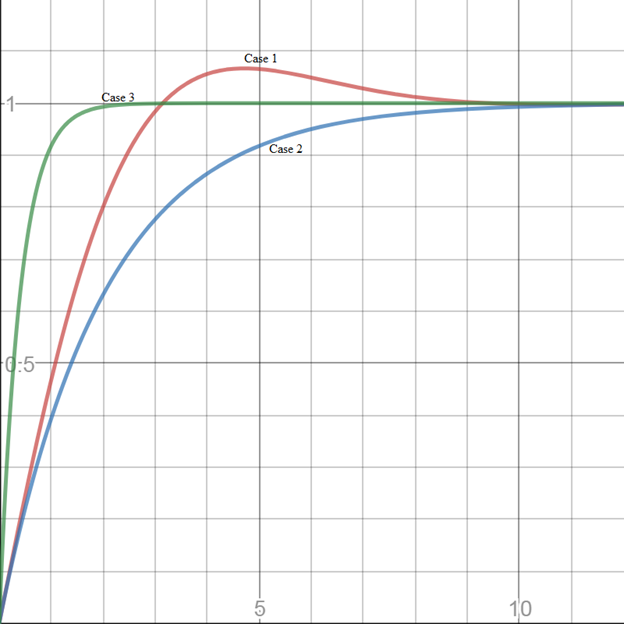
Here, on comparing the responses for all the three cases, it is concluded that the response shifts from being underdamped to overdamped for the first two cases. Whereas, for the third case the response remains overdamped in nature however, its settling time is very less comparing the other two cases.

Conclusion:

At the damping ratio $\zeta =0.707$, there is a small overshoot encountered in the response while for the cases where damping ratios are1 and 1.34 respectively shows the overdamping in the response. And the response in first and second case are sluggish while the response for the third case is faster with the less settling time.