Chapter 9.3, Problem 36PPS

a.

To determine

To find the duration of time that the ball is in the air.

Answer to Problem 36PPS

The ball is in the air for 4.7 seconds.

Explanation of Solution

Given information :

The function provided for the path of the ball is $h=-16t^2+76t$ .

Formula used :

The given equation would be graphed as a function and the points of x-intercepts would be the results. For these points, the x-coordinate shall serve the purpose of the results.

Since the roots are not on points that are integers, use the approximation method to compute the roots.

Calculation :

Using the graphing calculator, the graph for the given function is:

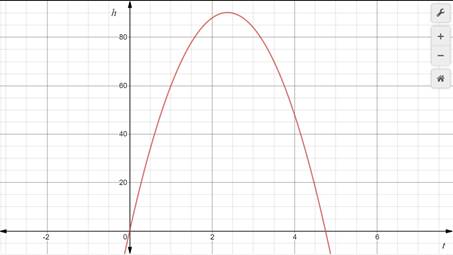
In this, the parabola one x-intercept at the origin and the other in between 4 and 5.

To find the roots, make a table of values for x in between these points with intervals on 0.1 . The value of x that is result closest to 0 will be the roots of the equation.

Table of values in between 4 and 5

X	4.1	4.2	4.3	4.4	4.5	4.6	4.7	4.8	4.9
Y	42.64	36.96	30.96	24.64	18	11.04	3.76	-3.84	-11.76

In the tables, the value of y that is closest to 0 is 3.76. Their corresponding x values would be the roots.

Thus, 4.7 the root. Hence the time taken to reach the ground is 4.7 seconds .

b.

To determine

To calculate the maximum height the ball reached.

Answer to Problem 36PPS

The maximum height that the ball reached is 90.25 feet .

Explanation of Solution

Given information :

The function provided is $h=-16t^2+76t$ .

Formula used :

The maximum height attained by the ball can be calculated using the vertex formula. Here, find the y-coordinate of the point of the vertex. This value will be the maximum height attained by the golf ball.

Formula to compute equation of the axis of symmetry $x=-\frac{b}{2\times a}$ . Here, $a=-16$ and $b=76$ . ‘a’ and ‘b’ are coefficients $x^2$ and $x$ respectively. Use this value in the original function to derive the maximum distance travelled.

Calculation :

  $x=-\frac{b}{2\times a}$

Formula for axis of symmetry.

  $x=-\frac{76}{2\times \left(-16\right)}$

Putting the values of ‘a’ and ‘b’ .

  $=\frac{76}{32}$

Simplifying this

  $x=\frac{38}{16}or,2.375$ is the equation of axis of symmetry.

Vertex can be found out by putting the value of x computed in the axis of symmetry in the original function. This will give a value of y . These two coordinates of x and y would be the point where the vertex is.

  $=-16{\left(2.375\right)}^2+76\left(2.375\right)$

Putting the value of $x=2.375$ in the original function.

  $=-90.25+180.5$

Simplifying the expression.

  $=90.25$

Thus the maximum distance travelled north is 90.25feet .

c.

To determine

To calculate the time taken to reach maximum height by the ball reached.

Answer to Problem 36PPS

The maximum height that the ball reached is 2.375 seconds .

Explanation of Solution

Given information :

The function provided is $h=-16t^2+76t$ .

Formula used :

The time taken to reach the maxim height by the ball would be the x value of the equation of axis of symmetry.

Formula to compute equation of the axis of symmetry $x=-\frac{b}{2\times a}$ . Here, $a=-16$ and $b=76$ . ‘a’ and ‘b’ are coefficients $x^2$ and $x$ respectively. Use this value in the original function to derive the maximum distance travelled.

Calculation :

  $x=-\frac{b}{2\times a}$

Formula for axis of symmetry.

  $x=-\frac{76}{2\times \left(-16\right)}$

Putting the values of ‘a’ and ‘b’ .

  $=\frac{76}{32}$

Simplifying this

  $x=\frac{38}{16}or,2.375$ is the equation of axis of symmetry.

Thus the time taken by the ball to reach maximum height is 2.375 seconds.