Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
14th Edition
ISBN: 9780134677972
Author: Barnett
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 9.1, Problem 27E
In Problems 27-32, use the transition diagram
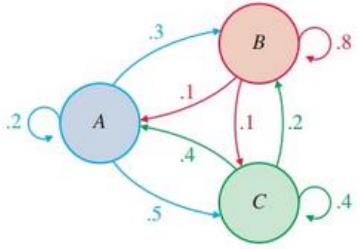
to find
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Ff.253.
H9.
2. A manufacturer has a machine that, when operational at the beginning of a day, has a probability of 0.1 of
breaking down sometime during the day. When this happens, the repair is done the next day and completed at
the end of that day.
The one-step transition matrix is obtained from Week 12 assignment Problem #3:
State O-operational, state 1 – break down, state 3 -- repaired
0.9 0.1 0
0
0 1
0.9
0.1 0
P =
(a) Use the approach described in Sec. 29.6 to find the 歭 (the expected first passage time from state i to state j)
for all i and j. Use these results to identify the expected number of full days that the machine will remain
operational before the next breakdown after a repair is completed.
(b) Now suppose that the machine already has gone 20 full days without a breakdown since the last repair was
completed. How does the expected number of full days hereafter that the machine will remain operational
before the next breakdown compare with the corresponding result from part (b) when…
Chapter 9 Solutions
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Ch. 9.1 - (A) Refer to the transition diagram in Figure 1....Ch. 9.1 - Refer to Example 4. States D and G are referred to...Ch. 9.1 - An insurance company classifies drivers as...Ch. 9.1 - Find P4 and use it to find S4 for AAP=AA.8.2.3.7...Ch. 9.1 - Use P8 and a graphing calculator to find S8 for P...Ch. 9.1 - Refer to Example 4. At the end of each year the...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...
Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 1-8, find the matrix product, if it is...Ch. 9.1 - In Problems 9-14, use the transition matrix...Ch. 9.1 - In Problems 9-14, use the transition matrix...Ch. 9.1 - In Problems 9-14, use the transition matrix...Ch. 9.1 - In Problems 9-14, use the transition matrix...Ch. 9.1 - In Problems 9-14, use the transition matrix...Ch. 9.1 - In Problems 9-14, use the transition matrix...Ch. 9.1 - In Problems 15-20, use the transition diagram to...Ch. 9.1 - In Problems 15-20, use the transition diagram to...Ch. 9.1 - In Problems 15-20, use the transition diagram to...Ch. 9.1 - In Problems 15-20, use the transition diagram to...Ch. 9.1 - In Problems 15-20, use the transition diagram to...Ch. 9.1 - In Problems 15-20, use the transition diagram to...Ch. 9.1 - In Problems 21-26, use the transition matrix...Ch. 9.1 - In Problems 21-26, use the transition matrix...Ch. 9.1 - In Problems 21-26, use the transition matrix...Ch. 9.1 - In Problems 21-26, use the transition matrix...Ch. 9.1 - In Problems 21-26, use the transition matrix...Ch. 9.1 - In Problems 21-26, use the transition matrix...Ch. 9.1 - In Problems 27-32, use the transition diagram to...Ch. 9.1 - In Problems 27-32, use the transition diagram to...Ch. 9.1 - In Problems 27-32, use the transition diagram to...Ch. 9.1 - In Problems 27-32, use the transition diagram to...Ch. 9.1 - In Problems 27-32, use the transition diagram to...Ch. 9.1 - In Problems 27-32, use the transition diagram to...Ch. 9.1 - Draw the transition diagram that corresponds to...Ch. 9.1 - Find the transition matrix that corresponds to the...Ch. 9.1 - Draw the transition matrix that corresponds to the...Ch. 9.1 - Find the transition diagram that corresponds to...Ch. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - Prob. 42ECh. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - In Problems 37-44, could the given matrix be the...Ch. 9.1 - In Problems 45-50, is there a unique way of...Ch. 9.1 - In Problems 45-50, is there a unique way of...Ch. 9.1 - In Problems 45-50, is there a unique way of...Ch. 9.1 - In Problems 45-50, is there a unique way of...Ch. 9.1 - In Problems 45-50, is there a unique way of...Ch. 9.1 - In Problems 45-50, is there a unique way of...Ch. 9.1 - In Problems 51-56, are there unique values of a,b,...Ch. 9.1 - In Problems 51-56, are there unique values of a,b,...Ch. 9.1 - In Problems 51-56, are there unique values of a,b,...Ch. 9.1 - Prob. 54ECh. 9.1 - In Problems 51-56, are there unique values of a,b,...Ch. 9.1 - Prob. 56ECh. 9.1 - In Problems 57-60, use the given information to...Ch. 9.1 - A Markov chain has two states, A and B. The...Ch. 9.1 - Prob. 59ECh. 9.1 - Prob. 60ECh. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - Prob. 65ECh. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - Prob. 67ECh. 9.1 - Prob. 68ECh. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - Problems 61-70 refer to the following transition...Ch. 9.1 - In Problems 71-74, given the transition matrix P...Ch. 9.1 - In Problems 71-74, given the transition matrix P...Ch. 9.1 - In Problems 71-74, given the transition matrix P...Ch. 9.1 - In Problems 71-74, given the transition matrix P...Ch. 9.1 - A Markov chain with two states has transition...Ch. 9.1 - Repeat Problem 75 if the initial-state matrix is...Ch. 9.1 - Given the transition matrix...Ch. 9.1 - Prob. 78ECh. 9.1 - Show that if P=a1a1bb is probability matrix, then...Ch. 9.1 - Show that if P=a1a1bbandS=c1c are probability...Ch. 9.1 - Use a graphing calculator and the formula Sk =...Ch. 9.1 - Use a graphing calculator and the formula Sk=S0Pk...Ch. 9.1 - Use a graphing calculator and the formula Sk=S0Pk...Ch. 9.1 - Use a graphing calculator and the formula Sk=S0Pk...Ch. 9.1 - Scheduling. An outdoor restaurant in a summer...Ch. 9.1 - Scheduling. Repeat Problem 85 if the probability...Ch. 9.1 - Advertising. A television advertising campaign is...Ch. 9.1 - Car rental. A car rental agency has facilities at...Ch. 9.1 - Homeowner's insurance. In a given city, the market...Ch. 9.1 - Service contracts. A small community has two...Ch. 9.1 - Travel agent training. A chain of travel agencies...Ch. 9.1 - Welder training. All welders in a factory begin as...Ch. 9.1 - Health plans. A midwestern university offers its...Ch. 9.1 - Dental insurance. Refer to Problem 93. During the...Ch. 9.1 - Housing trends. The 2000 census reported that 41.9...Ch. 9.1 - Housing trends. The 2000 census reported that 66.4...Ch. 9.2 - (A) Suppose that the toothpaste company started...Ch. 9.2 - Which of the following matrices are regular? (A)...Ch. 9.2 - The transition matrix for a Markov chain is...Ch. 9.2 - Refer to Matched Problem 1 in Section 9.1, where...Ch. 9.2 - A mail-order company classifies its customers as...Ch. 9.2 - Repeat Example 5 for P=.3.6.1.2.3.5.1.2.7Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 1-8. without using a calculator, find...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - Prob. 13ECh. 9.2 - Prob. 14ECh. 9.2 - Prob. 15ECh. 9.2 - Prob. 16ECh. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - In Problems 9-22, could the given matrix be the...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - For each transition matrix P in Problems 23-30,...Ch. 9.2 - Problems 31-34 refer to the regular Markov chain...Ch. 9.2 - Problems 31-34 refer to the regular Markov chain...Ch. 9.2 - Problems 31-34 refer to the regular Markov chain...Ch. 9.2 - Problems 31-34 refer to the regular Markov chain...Ch. 9.2 - In Problems 35-40, discuss the validity of each...Ch. 9.2 - In Problems 35-40, discuss the validity of each...Ch. 9.2 - In Problems 35-40, discuss the validity of each...Ch. 9.2 - In Problems 35-40, discuss the validity of each...Ch. 9.2 - In Problems 35-40, discuss the validity of each...Ch. 9.2 - In Problems 35-40, discuss the validity of each...Ch. 9.2 - In Problems 41-44, approximate the stationary...Ch. 9.2 - In Problems 41-44, approximate the stationary...Ch. 9.2 - In Problems 41-44, approximate the stationary...Ch. 9.2 - In Problems 41-44, approximate the stationary'...Ch. 9.2 - A red urn contains 2 red marbles and 3 blue...Ch. 9.2 - Repeat Problem 45 if the red urn contains 5 red...Ch. 9.2 - Given the transition matrix P=0110 A) Discuss the...Ch. 9.2 - Given the transition matrix P=001100010 (A)...Ch. 9.2 - The transition matrix for a Markov chain is...Ch. 9.2 - The transition matrix for a Markov chain is...Ch. 9.2 - Problems 51 and 52 require the use of a graphing...Ch. 9.2 - Problems 51 and 52 require the use of a graphing...Ch. 9.2 - The transition matric for a Markov chain is...Ch. 9.2 - The transition matric for a Markov chain is...Ch. 9.2 - Transportation. Most railroad cars are owned by...Ch. 9.2 - Transportation. The railroad in Problem 55 also...Ch. 9.2 - Labor force. Table 1 gives the percentage of the...Ch. 9.2 - Home ownership. The U.S. Census Bureau published...Ch. 9.2 - Market share. Consumers can choose between three...Ch. 9.2 - Market share. Consumers in a certain area can...Ch. 9.2 - Insurance. An auto insurance company classifies...Ch. 9.2 - Insurance. Repeat Problems 61 if 40 of preferred...Ch. 9.2 - Problems 63 and 64 require the use of a graphing...Ch. 9.2 - Problems 63 and 64 require the use of a graphing...Ch. 9.2 - Genetics. A given plant species has red, pink, or...Ch. 9.2 - Gene mutation. Suppose that a gene in a chromosome...Ch. 9.2 - Rapid transit. A new rapid transit system has just...Ch. 9.2 - Politics: filibuster. The Senate is in the middle...Ch. 9.2 - The population center of the 48 contiguous states...Ch. 9.2 - The population center of the 48 contiguous states...Ch. 9.3 - (A) For the initial-state matrix S0=abc, find the...Ch. 9.3 - Determine whether each statement is true or false....Ch. 9.3 - Identify any absorbing states for the following...Ch. 9.3 - Use a transition diagram to determine whether P is...Ch. 9.3 - Repeat Example 3 if 10 of farmers sell to company...Ch. 9.3 - Repeat Example 4 for the standard form P found in...Ch. 9.3 - Repeat Example 5 for the following transition...Ch. 9.3 - In Problems 1-6, identify the absorbing states in...Ch. 9.3 - In Problems 1-6, identify the absorbing states in...Ch. 9.3 - In Problems 1-6, identify the absorbing states in...Ch. 9.3 - In Problems 1-6, identify the absorbing states in...Ch. 9.3 - In Problems 1-6, identify the absorbing states in...Ch. 9.3 - In Problems 1-6, identify the absorbing states in...Ch. 9.3 - In Problems 7-10, identify the absorbing states...Ch. 9.3 - In Problems 7-10, identify the absorbing states...Ch. 9.3 - In Problems 7-10, identify the absorbing states...Ch. 9.3 - In Problems 7-10, identify the absorbing states...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 11-20, could the given matrix be the...Ch. 9.3 - In Problems 21-24.find a standard form for the...Ch. 9.3 - In Problems 21-24.find a standard form for the...Ch. 9.3 - In Problems 21-24.find a standard form for the...Ch. 9.3 - In Problems 21-24.find a standard form for the...Ch. 9.3 - In Problems 25-28, find a standard form for the...Ch. 9.3 - In Problems 25-28, find a standard form for the...Ch. 9.3 - In Problems 25-28, find a standard form for the...Ch. 9.3 - In Problems 25-28, find a standard form for the...Ch. 9.3 - In Problems 29-34, find the limiting matrix for...Ch. 9.3 - In Problems 29-34, find the limiting matrix for...Ch. 9.3 - In Problems 29-34, find the limiting matrix for...Ch. 9.3 - In Problems 29-34, find the limiting matrix for...Ch. 9.3 - In Problems 29-34, find the limiting matrix for...Ch. 9.3 - In Problems 29-34, find the limiting matrix for...Ch. 9.3 - Problems 35-40 refer to the matrices in Problems...Ch. 9.3 - Problems 35-40 refer to the matrices in Problems...Ch. 9.3 - Problems 35-40 refer to the matrices in Problems...Ch. 9.3 - Problems 35-40 refer to the matrices in Problems...Ch. 9.3 - Problems 35-40 refer to the matrices in Problems...Ch. 9.3 - Problems 35-40 refer to the matrices in Problems...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 41-48, discuss the validity of each...Ch. 9.3 - In Problems 49-52, use a graphing calculator to...Ch. 9.3 - In Problems 49-52, use a graphing calculator to...Ch. 9.3 - In Problems 49-52, use a graphing calculator to...Ch. 9.3 - In Problems 49-52, use a graphing calculator to...Ch. 9.3 - The following matrix P is a nonstandard transition...Ch. 9.3 - Repeat Problem 53 for...Ch. 9.3 - Verify the results in Problem 53 by computing Pk...Ch. 9.3 - Verify the results in Problem 54 by computing Pk...Ch. 9.3 - Show that S=x1x0,0x1, is a stationary matrix for...Ch. 9.3 - Show that S=x1x00,0x1, is a stationary matrix for...Ch. 9.3 - An absorbing Markov chain has the following matrix...Ch. 9.3 - Refer to the matrices P and Q of Problem 59. For k...Ch. 9.3 - Loans. A credit union classifies car loans into...Ch. 9.3 - Employee training. A chain of car muffler and...Ch. 9.3 - Marketing. Three electronics firms are...Ch. 9.3 - Pensions. Once a year company employees are given...Ch. 9.3 - Medicine. After bypass surgery, patients are...Ch. 9.3 - Medicine. The study discussed in Problem 65 also...Ch. 9.3 - Psychology. A rat is placed in room F or room B of...Ch. 9.3 - Psychology. Repeat Problem 67 if the exit from...Ch. 9 - Given the transition matrix P and initial-state...Ch. 9 - In Problems 2-6, P is a transition matrix for a...Ch. 9 - In Problems 2-6, P is a transition matrix for a...Ch. 9 - In Problems 2-6, P is a transition matrix for a...Ch. 9 - In Problems 2-6, P is a transition matrix for a...Ch. 9 - Prob. 6RECh. 9 - In Problems 7-10, write a transition matrix for...Ch. 9 - In Problems 7-10, write a transition matrix for...Ch. 9 - In Problems 7-10, write a transition matrix for...Ch. 9 - In Problems 7-10, write a transition matrix for...Ch. 9 - A Markov chain has three states, A,B, and C. The...Ch. 9 - Given the transition matrix ABP=AB.4.6.9.1 find...Ch. 9 - In Problems 13 and 14. solve the equation SP=S to...Ch. 9 - In Problems 13 and 14. solve the equation SP=S to...Ch. 9 - In Problems 15 and 16, find the limiting matrix...Ch. 9 - In Problems 15 and 16, find the limiting matrix...Ch. 9 - In Problems 17-20, use a graphing calculator to...Ch. 9 - In Problems 17-20, use a graphing calculator to...Ch. 9 - In Problems 17-20, use a graphing calculator to...Ch. 9 - In Problems 17-20, use a graphing calculator to...Ch. 9 - Find a standard form for the absorbing Markov...Ch. 9 - In Problems 22 and 23, determine the long-run...Ch. 9 - In Problems 22 and 23, determine the long-run...Ch. 9 - Let P be a 22 transition matrix for a Markov...Ch. 9 - Let P be a 33 transition matrix for a Markov...Ch. 9 - A red urn contains 2 red marbles, 1 blue marble,...Ch. 9 - Repeat Problem 26 if the blue and green marbles...Ch. 9 - Show that S=xyz0, where 0x1, 0y1, 0z1, and...Ch. 9 - Give an example of a transition matrix for a...Ch. 9 - Give an example of a transition matrix for an...Ch. 9 - Give an example of a transition matrix for a...Ch. 9 - Give an example of a transition matrix for an...Ch. 9 - Explain why an absorbing Markov chain that has...Ch. 9 - Explain why a regular Markov chain that has more...Ch. 9 - A Markov chain has transition matrix P=.4.6.2.8...Ch. 9 - In Problems 36 and 37, use a graphing calculator...Ch. 9 - In Problems 36 and 37, use a graphing calculator...Ch. 9 - Product switching. A company's brand X has 20 of...Ch. 9 - Marketing. Recent technological advances have led...Ch. 9 - Prob. 40RECh. 9 - Employee training. In order to become a fellow of...Ch. 9 - Genetics. A given plant species has red, pink, or...Ch. 9 - Smoking. Table 2 gives the percentage of U.S....
Additional Math Textbook Solutions
Find more solutions based on key concepts
In Problems 1-14, solve the given initial value problem using the method of Laplace transforms. y2y+5y=0; y(0)=...
Fundamentals of Differential Equations and Boundary Value Problems
ASSESSMENT Find the first five terms in sequences with the following nth terms. a. n2+2 b. 5n+1 c. 10n1 d. 3n2 ...
A Problem Solving Approach to Mathematics for Elementary School Teachers (12th Edition)
The table by using the given graph of h.
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Coin Tosses An experiment consists of tossing a coin four times and observing the sequence of heads and tails. ...
Finite Mathematics & Its Applications (12th Edition)
CHECK POINT I Express as a percent.
Thinking Mathematically (7th Edition)
Referring to Exercise 2.95, what is the probability that a person diagnosed as having cancer actually has the d...
Probability and Statistics for Engineers and Scientists
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 2. Suppose that in Example 2.27, 400 units of food A, 500 units of B, and 600 units of C are placed in the test tube each day and the data on daily food consumption by the bacteria (in units per day) are as shown in Table 2.7. How many bacteria of each strain can coexist in the test tube and consume all of the food? Table 2.7 Bacteria Strain I Bacteria Strain II Bacteria Strain III Food A 1 2 0 Food B 2 1 3 Food C 1 1 1arrow_forwardstate 1[.1 .1 .8 1. Consider the transition matrix P= state 2.5 5 0 state 3.7 0 3 a. Identify what the entry in row one, column three (the .8) represents: b. Find p (use your calculator. no work required): c. Identify what the entry in row two, column one of represents.arrow_forward2.Initially we have 2 red marbles in Box 1 and 2 white marble in Box 2. At every time step, we take a marble from each box and swap. Let Xt be the number of red marbles in Box 1 at time t. There are 3 states: 0, 1, 2. Let P be the transition matrix for {X;}, what is (P)oo (probability from state 0 to state 0)?arrow_forward
- Number 20 in the image attachedarrow_forwardLet us have the experience of a mouse falling into a trap inside a 6-room building, as shown in the figure below. If the room contains k doors, the probability that the mouse will choose one of these doors is 1/k if the mouse reaches room F that contains the food or room S that contains the trap. It will stay there and the experiment ends, the transition matrix is M= [0.5 0 0.5 0 0.3 0 0 ¹0.5 0 0 0.3 0.3 0 0.3 0.3 0 0.5 0 000 O a O b О с 2 000 0.5 0 0.5 0 0 0 0 0.3 0 0.5 0 0.5 M = - 0 0.5 0.5 b 3 ..+. 4 5 0 0 S M= 0 0 0 1 0 0.5 0 0 0 0 0.5 0 0 0.3 0.3 0 0 0.3 0 0.5 0 0 0.5 0 0 1 00000 10 0 000 0.5 0 0 0.5 0 0.3 0 0.3 0.3 0 0.3 0.3 0 0 0 0.5 0 0 000 0 0 0 0 C 0 0 0.3 0.5 1 (a)arrow_forwardConsider a communication channel where each substation transmits and receive data. The probability between the substations is shown in figure 3. 0.4 0.5 0.3 0.2 2 2 0.3 Figure 3 i. Draw a transition diagram. ii. Write down a transition matrix, P. iii. Name the type of matrix in Q3(b) P(X, =2 X, = 1|X, =3) iv. P(X, =2 X, = 3X, =2) V. enarrow_forward
- 5. consider the example below, where the states are Condition State and the transition matrix is 0 1 23 2 Πο Good as new Operable-minimum deterioration Operable-major deterioration Inoperable and replaced by a good-as-new machine we found that the steady-state probabilities are 2 13' T1= = P = 78314 00 1 0 7 13' HARTNO LELBLINO 1 16 1 1 1 1 16 8 8 0 2 2 = π2 2 13' I3 = 2 13 (a) Find the expected recurrence time for state 0 (i.e., the expected length of time a machine can be used before it must be replaced) by solving a linear system for Moo, M10, 20, and μ30. (b) Find the expected recurrence time for state O directly by the formula Moo 1 πο =arrow_forwardFor a transition matrix for a problem about people migrating from one region to another, O the columns will sum to 1 if there are no new people added to the system. if the number of people increase both rows and columns must sum to more than 1. O either the rows always sum to 1 or the columns always sum to 1 but not both. the rows will sum to 1 when the populations increase linearly. Question 5 ( , Find the answer that selects all the true statements about trace. a) If A = then tr(A) = 16. %3D b) If A and conform for multiplication in either order, then tr(AB) = tr(BA). c) If C conforms with A for multiplication CA, and A and B have the same dimensions, then tr(C(A + B)) = tr(C)tr(A) + tr(B)tr(C). d) If A and B conform for multiplication AB and C have the same dimensions as AB then tr(AB + C = tr(A)tr(B) + tr(C). Both c) and d).arrow_forward3. A study has determined that the occupation of a boy, as an adult, depends upon the occupation of his father and is given by the following transition matrix where P= professional, F= farmer and L= laborer Father's Occupation P F L 0.80 0.30 0.20 0.10 0.50 0.20 0.10 0.20 0.60 P Son's F Occupationarrow_forward
- Milan.sttarrow_forward3. A rat is put into the following maze: 3 moves. 1 2 The rat has a probability of 1/4 of starting in any compartment and suppose that the rat chooses a passageway at random when it makes a move from one compartment to another at each time. Let Xn be the compartment occupied by the rat after n (a) Explain why {X₂} is a MC and find the transition matrix P. (b) Explain why the chain is irreducible, aperiodic and positive recurrent. (c) What is the limit of Pn? Explain. (d) Find the probability that the rat is in compartment 3 after two moves. (e) In the long run, how many times that the rat enters in compartment 4 in 100 movements?arrow_forwardConsider a communication channel where each substation transmits and receive data. The probability between the substations is shown in figure 3. 0.4 0.5 0.3 0.2 2 2 3 0.3 Figure 3 i. Draw a transition diagram. ii. Write down a transition matrix, P. iii. Name the type of matrix in Q3(b) P(X; =2 X,=1\X, =3) iv. P(X; =2 _X,=3{X, =2) V.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Finite Math: Markov Chain Example - The Gambler's Ruin; Author: Brandon Foltz;https://www.youtube.com/watch?v=afIhgiHVnj0;License: Standard YouTube License, CC-BY
Introduction: MARKOV PROCESS And MARKOV CHAINS // Short Lecture // Linear Algebra; Author: AfterMath;https://www.youtube.com/watch?v=qK-PUTuUSpw;License: Standard Youtube License
Stochastic process and Markov Chain Model | Transition Probability Matrix (TPM); Author: Dr. Harish Garg;https://www.youtube.com/watch?v=sb4jo4P4ZLI;License: Standard YouTube License, CC-BY