Chapter 9.2, Problem 58E

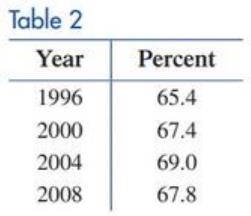
Home ownership. The U.S. Census Bureau published the home ownership rates given in Table 2.

The following transition matrix $P$ is proposed as a model for the data, where $H$ represents the households that own their home.

$\begin{array}{l}\text{ Four years later}\\ \begin{array}{cc}H& H^{\prime }\end{array}\\ \begin{array}{c}\text{Current}\\ \text{year}\end{array}\begin{array}{c}H\\ H^{\prime }\end{array}\left[\begin{array}{cc}.95& .05\\ .15& .85\end{array}\right]=P\end{array}$

(A) Let $S_0=\left[\begin{array}{cc}.654& .346\end{array}\right]$, and find $S_1,S_2$, and $S_3$. Compute both matrices exactly and then round entries to three decimal places.

(B) Construct a new table comparing the results from part (A) with the data in Table 2.

(C) According to this transition matrix, what percentage of households will own their home in the long run?